по трэс

		n			n
M x =		∑ xi , M y =			∑ yi / N ,
	i=1			i=1
K xy	n		− M (x))(yi −
	= ∑ (xi					M ( y))/ N ,
	i =1
				n
	Dxy =			∑ (xi − M (x))2			/ N .
			i=1

Линейная зависимость, связывающая x и y, имеет вид

	K	xy		K	xy
y =			+ M ( y) −			M (x) x .
	Dx			Dx

Пример. Температура жала паяльника зависит от напряжения нагревателя (табл. 4.1).

Табл. 4.1. Температура жала паяльника

Напряжение питания, В	32	36	38	40	42	46	48
Температура, °С	225	240	250	255	260	270	280

(4.3)

(4.4)

(4.5)

В результате расчета по формулам (4.2) — (4.5) получено уравнение регрессии следующего вида: T = 122,6 + 3,27U. При U = 40 В рас-

четная температура жала 253,4 °С.

Преимущество пассивного эксперимента состоит в том, что при его применении нет необходимости тратить время и средства на постановку опыта. Однако такой эксперимент имеет существенные недостатки, ограничивающие его применение для оптимизации ТП. Во-первых, интервалы варьирования технологическими факторами обычно малы, поэтому изменения выходной величины будут в большей степени зависить от воздействия неконтролируемых случайных возмущений. Во-вторых, при пассивном эксперименте в производственных условиях часто не рассматриваются факторы, оказывающие существенное влияние на процесс, из-за невозможности их измерения или регистрации.

4.2. ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ

От перечисленных выше недостатков свободен активный эксперимент, который ставится по заранее разработанному плану. К основным преимуществам активного эксперимента можно отнести:

∙четкую логическую схему проведения всего процесса исследования;

∙сокращение объема экспериментальных исследований, повышение надежности интерпретации полученных результатов;

∙формализацию процесса построения модели и возможность ее оптимизации.

Одним из активных методов планирования экстремальных экспериментов является полный факторный экс- перимент (ПФЭ), при котором модель процесса представляет полином:

k	k
y = b0 + ∑ bi xi +	∑ bij xi x j .
i=1	i¹ j

Центр плана, т. е. точка, в окрестностях которой ставится серия опытов, выбирается на основе априорных сведений о процессе. Для удобства обработки результатов опыта вводится кодирование независимых входных факторов Xi:

Xi = (xi − x0i )/ xi ,

68

где xi — натуральное значение фактора; x0i — базовый, или начальный, уровень i-го фактора; xi — шаг варьирования по i-му фактору.

Для независимых факторов, имеющих два уровня, верхний обозначают +1, нижний –1. В ПФЭ реализуются все возможные сочетания уровней факторов. Если число уровней каждого фактора равно двум (верхний и нижний), то общее число опытов N = 2k, где k — число факторов. Для простоты записи кодированных значений факторов +1 и –1 единицы опускают. Условия эксперимента записывают в виде матрицы планирования эксперимента, где строки соответствуют различным опытам, а столбцы — значениям факторов. Условная переменная X0, которая в процессе опыта имеет значение +1, вводится для удобства вычислений.

ПФЭ обладает тремя важными свойствами:

∙ симметричностью относительно центра эксперимента, т. е. алгебраическая сумма элементов векторстолбцов каждого фактора равна нулю:

N

∑Xij = 0,

i=1

где i — номер опыта; j — номер фактора ( j =1,k );

∙ условием нормировки, когда сумма квадратов элементов каждого столбца равна числу опытов как следствие того, что значения факторов в матрице задаются равными –1 и +1:

N

∑ X ij2 = N; i=1

∙ ортогональностью матрицы, т. е. сумма почленных произведений любых двух факторов-столбцов матрицы равна нулю:

N

∑ X ij X ui = 0, u = 0, k . i=1

После выполнения ПФЭ осуществляют независимую оценку коэффициентов полинома:

N

N

N

∑ y

i

∑ x y

i

∑ xi x j yi

i =1

i

i ¹ j

b =

,

b =

i =1

, b

=

,

0

N

i

N

ij

N

где yi — среднее значение выходного параметра по результатам параллельных опытов.

Далее определяют дисперсии среднего арифметического в каждой строке матрицы, которые должны быть однородны:

		2
Si2 = 1	∑(yi −		i )	,
		y
	m

m −1 i=1

где m — количество параллельных опытов.

Если одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден, когда число опытов во всех точках одинаково. При этом рассчитывают дисперсии в каждой горизонтальной строке матрицы Si2 , а затем из всех дисперсий выбирают наибольшую Smax2 , рассчитывают критерий Кохрена

= 2 { } N 2

G Smax y / ∑ Si

i=1

и сравнивают с табличным значением в зависимости от выбранного уровня вероятности Р (табл. 4.2). Если табличное значение критерия больше, чем рассчитанное, то дисперсии однородны. Дисперсия всего эксперимента

69

							N
			S 2	( y) = ( ∑ Si2 ) / N .
							i=1
		Табл. 4.2. Значения критерия Кохрена для P = 0,05
							N
G
	1	2	3				4	5	6	7
2	0,9958	0,9750	0,9392				0,9057	0,8772	0,8332	0,7880
3	0,9669	0,8709	0,7977				0,7457	0,7071	0,6530	0,6025
4	0,9065	0,7674	0,6841				0,6287	0,5895	0,5365	0,4884

При ортогональном планировании дисперсии ошибок определения каждого из коэффициентов равны между собой:

σ2{bi } = S 2 {yi }/ N .

Оценка достоверности коэффициентов регрессии производится с помощью критерия Стьюдента (t). Если bi<tтабл σ(bi), то коэффициент считается незначимым. Значения критерия Стьюдента определяются в зависимости от числа степеней свободы f1=N(m–1) и выбранного уровня значимости (табл.4.3).

Табл. 4.3. Квантили распределения Стьюдента tтабл

f	P=0,05	P=0,01
8	2,31	3,36
12	2,18	3,05
16	2,12	2,92
24	2,06	2,80
30	2,04	2,75

Для оценки адекватности полученной математической модели, т. е. достаточно полного качественного и количественного описания процесса, используют критерий Фишера (F). Для этого оценивают дисперсию адекватности:

	σ2	=	1
			N − d
	ад

N					2
∑	y			i	− y		,
						i
i =1

где d — число членов в уравнении регрессии, за исключением b0; y i — значение выходного параметра, полу-

ченное расчетным путем из математической модели. Затем находят F - критерий:

F= σад2 / S 2 y .

Если F<Fтабл, то модель признается адекватной. Значение Fтабл выбирается в зависимости от числа степеней свободы f1=N– d и f2=N(m–1) ( табл.4.4).

Табл. 4.4. Значения F0,05 (верхние значения) и F0,01 (нижние значения)

				f1
	f2	4	5	6	7	8
	10	3,48	3,33	3,22	3,14	3,07
		5,99	5,64	5,39	5,20	5,06
	20	2,87	2,71	2,60	2,51	2,45
		4,43	4,10	3,87	3,70	3,56

70

				а				b
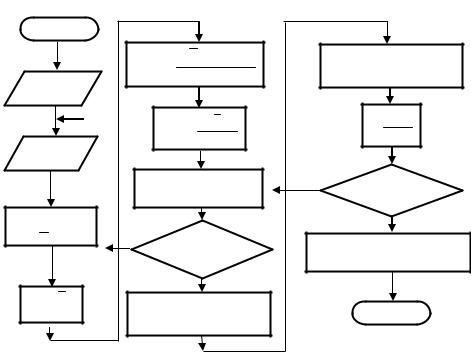
	Начало
			B(I,J) = ∑Y(I) − X(I,J)					Вычисление
									2
	Ввод				N
								Sад
	X(I,J)
	с			S 2(Y) = S	2	Y (I )		Sад2
								F =	2	(Y)
	Ввод					N		S
	Y(I,J)
				Вычисление			Нет	F – F табл<0
				t(I)		с
Вычисление										Да
			Нет
	Y(I)	с		t(I) – t кр<0				Печать
								Y i = B 0 + ∑B (I , J ) X ( I , J )
	= ∑ Y(I)				Да
B0			Y ( I ) = B 0 + ∑B ( I ) X ( I ) +					Конец
	N		+ ∑B ( I , J ) X (I , J )
а				b

Рис. 4.1. Алгоритм получения математической модели на ЭВМ

Если условие не выполняется, то модель считается неадекватной. Для получения адекватной модели необходимо сузить интервалы варьирования, увеличить количество параллельных опытов m и повторить ПФЭ. Для ускорения процессов вычисления статистических характеристик используется ЭВМ. Алгоритм получения математической модели по стандартной подпрограмме приведен на рис. 4.1.

После проведения ПФЭ и обработки результатов дальнейшие действия должны сводиться к нахождению оптимальных сочетаний факторов, чтобы приблизить данный процесс к оптимальному. На первом этапе по коэффициентам в уравнении регрессии судят о том, как сильно и в каком направлении влияет каждый фактор на параметр оптимизации. Увеличение фактора при положительном коэффициенте увеличивает значение функции y, увеличение факторов при отрицательном коэффициенте уменьшает значение функции. Абсолютные значения коэффициентов возрастают с увеличением интервалов варьирования.

Далее анализируются эффекты взаимодействия. Если эффект взаимодействия двух факторов имеет положительный знак, то для увеличения значения функции y требуется одновременное увеличение или уменьшение значений факторов, а для уменьшения значения y значения факторов должны одновременно изменяться в разных направлениях.

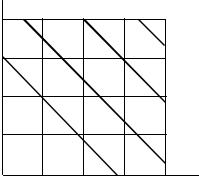
Графическая интерпретация уравнения регрессии осуществляется на плоскости x1, x2 при x3 = const. На втором этапе переходят к оптимизации математической модели различными методами.

71

x2

1

Y=13

0,5

Y=12

0

Y=11

-0,5

Y=10

-1					x1
-1	-0,5	0	0,5	1

Рис. 4.2. Поверхность отклика функции

Пример. Рассмотрим ПФЭ процесса УЗ-микросварки проволочных алюминиевых выводов толщиной 35 мкм к контактным площадкам, покрытым гальваническим сплавом Ni—In с целью замены золотого покрытия. Критерий оптимизации — прочность микросварного соединения на разрыв Р, сН. В качестве независимых технологических факторов были выбраны: x1 — электрическая мощность на выходе УЗгенератора (P, Вт); x2 — время УЗ-сварки (t, с); x3 — статическая нагрузка на УЗ-инструмент (F, г). Начальные условия эксперимента и матрица планирования приведены в табл. 4.5.

Табл. 4.5. Начальные условия и матрица планирования процесса УЗ-микросварки

Значения факторов

x1, P

x2, t

x3, F

Основной уровень xi

0,20

0,20

20

Интервал варьирования

xi

0,05

0,05

5

Верхний уровень (+1)

0,25

0,25

25

Нижний уровень (– 1)

0,15

0,15

15

Номер опыта

x0

x 1

x 2

x 3

x 1 x 2

x 2 x 3

x 1 x 3

x 1 x 2 x 3

y

i

S i2 {y }

1

+

–

–

–

+

+

+

–

5,29

0,65

2

+

+

–

–

–

+

–

+

7,90

0,76

3

+

–

+

–

–

–

+

+

7,70

1,06

4

+

+

+

–

+

–

–

–

9,43

1,81

5

+

–

–

+

+

–

+

+

9,00

1,92

6

+

+

–

+

–

–

–

–

11,33

2,20

7

+

–

+

+

–

+

+

–

12,16

3,45

8

+

+

+

+

+

+

–

+

15,74

3,81

После математической обработки данных получаем полином (уравнение регрессии): y = 9,81 + 1,42x1 + 1,27x2 + 2,21x3 + 0,05x1x2 + 0,18x2 x3 + 0,44x1x3 − 0,26x1x2 x3 .

Так как f1 = 8(3–1) = 16, то при уровне значимости 0,05 tтабл = 2,12, а bкр = tкрs{bi }= 2,12 × 0,495 = 1,02 . После исключения незначимых членов получаем искомое уравнение регрессии: y = 9,81 +1,42x1 +1,27 x2 + 2,21x3 .

В примере для 5%-го уровня значимости и f1 = 5, f2 = 16, Fтабл = 4,6Fрасч= 4,05 < Fтабл. Таким образом, полученная модель является адекватной. Графическая интерпретация уравнения регрессии осуществляется на плоскости x1, x2 при x3 = const = 0,5 (рис. 4.2).

4.3. ОПТИМИЗАЦИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

Задача оптимизации сводится к нахождению таких условий проведения ТП, при которых критерий оптими-

зации достигает экстремума. Функцию y = ϕ(x1, x2, ..., xn), связывающую критерий оптимизации с входными параметрами, варьируемыми при исследовании, принято называть функцией отклика, а геометрическое изображение функции отклика в факторном пространстве — поверхностью отклика. Экстремальное значение отклика достигается многократным последовательным продвижением в факторном пространстве несколькими методами.

72

1. Метод Гаусса— Зайделя. Последовательное продвижение осуществляется путем поочередного варьирования каждым фактором до достижения частного экстремума целевой функции. В каждой серии опытов изменяется только переменная xi, остальные остаются неизменными. Изображающая точка перемещается попеременно

вдоль каждой из координатной осей xi (i=1, k ) факторного пространства. Переход к новой (i+1)-й координате осуществляется при достижении частного экстремума целевой функции y(x) по предыдущей координате, т. е. в

точке xN+1, где dy(xN+1)/dxi = 0 (рис. 4.3, а).

Рис. 4.3. Движение в факторном пространстве в методах Гаусса-Зайделя (а) и градиента (б)

Направление движения вдоль (i+1)-й координатной оси выбирается обычно по результатам двух пробных экспериментов в окрестностях точки частного экстремума по предыдущей переменной. Поиск экстремума прекращается в точке, движение из которой в любом направлении не приводит к увеличению значения выходного параметра. При увеличении количества независимых пременных до 5—6 применение метода Гаусса— Зайделя для оптимизации ТП становится малоэффективным в силу увеличения числа экспериментов.

2. Метод градиента. При оптимизации градиентным методом движение совершается в направлении наибольшего изменения целевой функции, причем направление движения корректируется после каждого рабочего шага. Поскольку координатами вектора

	∂y		∂y			∂y
grad y(x) =		i;			j;...;			u
	∂x		∂x			∂x
				2			k
	1

служат коэффициенты при линейных членах уравнения регрессии b1, b2,...,bk, их можно определить по результатам нескольких пробных экспериментов в окрестностях исходной точки. В этом случае приращение целевой функции y, соответствующее приращению xi, можно считать пропорциональным значению частной производной:

	∂y	≈	y	= b (i =		) .
					1, k
	∂xi			i
			xi

После нахождения составляющих градиента выполняется рабочий шаг по направлению к экстремуму

(рис. 4.3, б):

x N +1 = x N + сшgrad y(x N ) ,

73

где ρш — мума γ:

параметр рабочего шага, который выбирают в зависимости от его номера h или расстояния от опти-

ρш = ρ/ (h γ) , где ρ — const; h — номер шага; 0 < γ < 0,5 (γ = 0,25) .

Показателем выхода в область оптимума является малое значение модуля градиента ( grad y(x) = 0 ), т. е. все коэффициенты bi становятся незначимыми или равными нулю. В градиентном методе важен выбор шага. При слишком малом шаге требуется большое количество экспериментов, а если размер шага велик, то можно "проскочить" оптимум.

3. Метод крутого восхождения (Бокса— Уилсона). Этот метод объединяет характерные элементы методов Гаусса— Зайделя и градиента. Так, шаговое движение при этом методе осуществляется в направлении наибольшего изменения функции (в направлении градиента), но в отличие от метода градиента корректировка направления движения производится не после каждого шага, а после достижения частного экстремума целевой функции, как при методе Гаусса— Зайделя. Практически поиск оптимума методом крутого восхождения выполняется следующим образом:

1)вблизи исходной точки x0 проводится эксперимент для определения grad y(x0), результаты эксперимента подвергаются статистическому анализу, определяются коэффициенты bi уравнения;

2)вычисляется произведение bi xi , где xi — шаг варьирования параметра xi при исследовании поверхности отклика в окрестностях исходной точки. Фактор, для которого произведение будет максимальным, принимается за базовый δб xб;

3)для базового фактора выбирается шаг движения λб по направлению к оптимуму, после этого вычисляются размеры шагов при крутом восхождении по остальным переменным процесса; при движении к оптимуму по градиенту все исследуемые параметры должны изменяться пропорционально коэффициентам наклона поверхности отклика bi:

λi = bi ki ;

bσ kσ

4)проводятся "мысленные" опыты, которые заключаются в вычислении по уравнению

y(x)= b0 + b1x1 + b2 x2 +... + bk xk

значений целевой функции в точках факторного пространства, лежащих на пути к экстремуму; при этом i-я координата n-й точки

x

n +1

= x

n

+ h

λi

,

xi

где h=

; i=

; λ

= b

= b +

xi

1, m

1, k

i

x

. Прогнозируемое значение выходного параметра

i

i

i

n

yпр = b0 + h∑bi

лi

;

Д x

i

5)поскольку каждый цикл крутого восхождения приближает к поверхности отклика с большой крутизной, рекомендуется для каждой последующей серии опытов выбирать шаг меньший, чем в предыдущей;

6)эксперимент прекращается, когда все или почти все коэффициенты bi уравнения получаются незначимыми или равными нулю, что говорит о выходе в область экстремума целевой функции.

Пример. Реализация крутого восхождения для оптимизации математической модели процесса УЗ-микросварки проволочных выводов

интегральных микросхем в виде y =	9,81+1,42x1 +1,27x2 + 2,21x3.
Определяем шаг варьирования:	i = xi /10 .

74

Шаг движения li = bi Di . Тогда l1 = 0,005×1,42 = 0,007,

l2 = 0,005×1,27 = 0,006,

l3 = 0,5 × 2,21=1,105 .

Находим значения факторов x в начале опыта:

x1¢ = x1ном + Dx1b1

= 0,15 + (0,005 ×1,42)= 0,157 ,

2 =

2

+ D

2 2

=

+

(0,005

×

1,27)

=

x¢

xном

+ D

x b

=

0,15

0,156 ,

3 =

3

3 3

+

(0,5

×

2,21)

=

x¢

xном

x b

10

11,1.

Начинаем "крутое восхождение" в сторону увеличения переменных х1, х2, х3, которые выбираем на уровне –1. Проводим "мысленные опыты", результаты которых заносим в табл. 4.6.

Табл. 4.6. Реализация "крутого восхождения"

Характеристики фактора и		Выходные факторы		Расчетное	Эксперимен-
номера опыта				~	тальные y
	x1 (P, Вт)	x 2 (t, c)	x 3 (F, cH)	y
Коэффициент bi	1,42	1,27	2,21	—	—
Шаг варьирования Di	0,005	0,005	0,5	—	—
Начальная точка:	0,15	0,15	10	—	—
в первом опыте	0,157	0,156	11,1	10,93	10,45
во втором опыте	0,164	0,162	12,2	12,04	11,60
в третьем опыте	0,171	0,168	13,3	13,16	12,42
в четвертом опыте	0,178	0,174	14,4	14,28	14,00
в пятом опыте	0,185	0,180	15,5	15,40	12,20
в шестом опыте	0,192	0,186	16,6	16,52	10,30

Наибольшее усилие отрыва Р = 14,00 сН в четвертом опыте. Оно подтверждается экспериментальными данными. В пятом опыте экспериментальное значение не подтверждается расчетным, поэтому "восхождение" прекращаем. Далее переходим к исследованию функции в стационарной области.

Шаговое движение к экстремуму продолжается до тех пор, пока не будет достигнута "почти стационарная" область, которая не может быть описана линейным выражением. Здесь сильнее проявляется взаимодействие факторов, характеризуемых коэффициентами при квадратичных членах полинома, поэтому ее обычно удается описать с достаточной точностью с помощью полинома второго порядка:

	k		+ ∑b x			k	2 .
y = b + ∑b x		i		x	j	+ ∑b x
0	i		ij i			ii	i
	i=1		ij			i=1

Для вычисления полинома второго порядка число уровней должно быть, как минимум, три, т. е. на единицу больше степени полинома. Однако применение ПФЭ типа 3k нерационально вследствие резкого увеличения объема экспериментов. Сократить их численность можно, используя так называемые центральные композици- онные планы (ЦКП). Их особенностью является добавление нескольких специально спланированных экспериментальных точек к матрице ПФЭ для получения плана второго порядка. При k факторах общее число опытов ЦКП

N = 2k + 2k + m0 ,

где 2k — " звездные" точки; m0 — число опытов в центре плана.

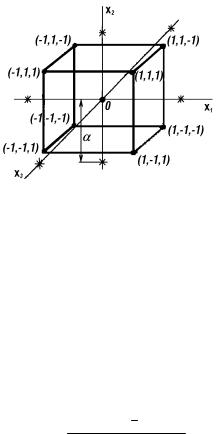
Таким образом к линейной модели добавляются так называемые "звездные" точки с координатами (0,

α),лежащие на сфере диаметром 2α (рис. 4.4), и опыты в центре плана. Бокс и Уилсон предложили выбирать плечо α и количество центральных точек (m0=1) так, чтобы план второго порядка оставался ортогональным (ЦКОП). При k = 3 он содержит всего 15 опытов, тогда как при ПФЭ 33 = 27. В силу ортогональности плана все коэффициенты определяются независимо друг от друга:

75

S 2 (y)

N

∑ xi yi

bi = i =1 N

∑ xi2

i =1

Рис. 4.4.

	N				N	N
	∑ xi x j				∑ (xi2	− ∑ xi2 / N )		i
		y	i				y
, b =	i=1			, b =	i=1	i=1			.	(4.6)
ij	N			ii	N	N
	∑ (xi x j )		2		∑ (xi2	− ∑ xi2 / N )	2
	i=1				i=1	i=1

Координационная решетка ЦКОП

В отличие от линейного полинома при ортогональном планировании второго порядка оценки коэффициен-

тов полинома находятся с неодинаковыми дисперсиями σ2{bi} = σ2{bij} по уравнению (4.6), а дисперсия при квадратичных членах уравнения регрессии — по формуле

σ2 {b }=
ii
N
∑ x2
	i
i =1

N	2		2 .
− ∑ x			/ N
i =1	i

Так же, как и при получении линейной модели, обработка результатов при реализации ЦКОП предполагает статистические проверки гипотез воспроизводимости результатов экспериментов, значимости коэффициентов и адекватности моделей.

Полученная модель второго порядка используется для нахождения оптимальных технологических режимов. Для этого модель методами аналитической геометрии приводится к канонической форме. При преобразовании прежде всего освобождаются от линейных членов путем переноса начала координат в точку O, соответствующую B0, затем от эффектов взаимодействия путем поворота осей координат вокруг точки O (см. рис. 4.4).

Для двух независимых переменных уравнение в канонической форме имеет вид

2	′	2	2	′	2	.
Y − Y01 = B11	(x1 )		+ B22	(x2 )
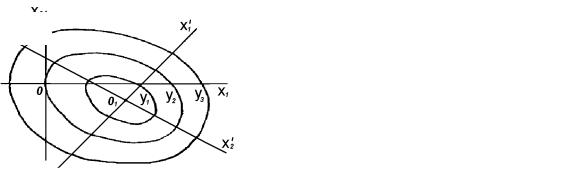
Поверхность отклика в зависимости от вида уравнения может быть трех типов. Если коэффициенты B11 и B22
имеют одинаковые знаки, то поверхность отклика —	эллиптический параболоид, центр которого — искомый

экстремум (рис. 4.5, а). В этом случае для нахождения оптимальной точки можно воспользоваться и не приве-

денным	уравнением второго порядка, для чего приравниваются нулю значения частных производных
∂Y / ∂xi	= bi + 2bij + bij x j = 0 и решается система уравнений. При разных знаках B11 и B22 поверхность отклика

относится к типу минимакса, или "седла". Для нахождения оптимальных технологических режимов нужно двигаться по благоприятному крылу "седла". Если один из коэффициентов Bij равен нулю, то поверхность отклика имеет форму нарастающего возвышения (рис. 4.5, б). Для отыскания оптимума следует двигаться по гребню, пока это допускают возможности ТП.

76

а		б

Рис. 4.5. Поверхности отклика функций:

а – эллиптическая; б – типа нарастающего возвышения

Пример. Начальные условия эксперимента и матрица ЦКОП приведены в табл. 4.7. В результате обработки экспериментальных данных на ПЭВМ получили уравнение регрессии следующего вида:

y =12,57 + 0,8x1 + 0,53x2 + 0,09x3 − 0,33x1x2 + 0,55x1x3 + 0,06x2 x3 + 1,07x1x2x3 − 1,79x12 − 1,13x22 − 1,86x32 .

Для уровня значимости 0,05 и числа степеней свободы f1 = N(m–1)=15(4–1) = 45 критерий Стьюдента t = 2,0. С учетом проверки значимости коэффициентов полинома по критерию Стьюдента уравнение приобретает вид

y =12,57 + 0,53x2 − 0,33x1 x2 + 0,55x1 x3 + 1,07 x1 x2 x3 −1,79 x12 −1,13x22 −1,86x32 .

Проверка полученной модели на адекватность с помощью F-критерия Фишера для уровня значимости 0,05 и числа степеней свободы f1

= N – α = 15–8 = 7, f2			Sад2 (		)	= 1,16 < 2,63 = F
	= N(m–1) = 15(4–1) = 45 показала, что F =			y					.
		p	S 2 (y)				табл
Таким образом, полученная модель адекватно описывает экспериментальные данные.
Для построения поверхности отклика составляем определитель:
		−1,79 − λ	−0,165				0,275
		− 0,165	− 1,13 − λ				0	= 0 .
		0,275	0				− 1,86 − λ

Решая определитель, получаем кубическое уравнение: λ3 + 4,78λ2 + 4,75λ + 3,627 = 0 .

Используя стандартную программу расчета на ПЭВМ,		находим корни уравнения: л1 = −1,089, л2 = −1,517, л3 = −2,120. Уравнение
поверхности отклика в каноническом виде имеет вид
x1			2	x2		2	x3				2
−				+			+				= 1 .
0,293				0,354			0,411

Графическая поверхность отклика имеет форму эллипсоида, полуоси которого: a = 0,293, b = 0,354, c = 0,411.

Табл. 4.7. Матрица центрального композиционного ортогонального плана

Значения факторов

x1

x2

x3

Основной уровень xi

0,13

0,125

5

Интервал варьирования xi

0,01

0,025

2

Верхний уровень (+1)

0,14

0,150

7

Нижний уровень (–1)

0,12

0,100

3

Номер опыта

x 0

x 1

x 2

x 3

x 12

x 22

x 32

S2(y)

y

1

+

+

+

+

+

+

+

13,74

0,62

2

+

+

–

+

+

+

+

12,83

0,08

3

+

–

+

+

+

+

+

12,75

0,57

4

+

–

–

+

+

+

+

11,30

0,37

5

+

+

+

–

+

+

+

12,00

0,39

6

+

+

–

–

+

+

+

12,04

0,71

7

+

–

+

–

+

+

+

13,94

0,77

8

+

–

–

–

+

+

+

12,00

0,46

77