
task_74895
.pdf



§ 28. Исследование временных рядов средствами вейвлет-анализа
Временной ряд — это функция от времени. Примеры временных ря- дов доставляют нам многие наблюдения природных и технических про- цессов: температура, вибрационные сигналы различных узлов металлооб- рабатывающего станка, количество осадков, курс рубля по отношению к евро.
Математическая подготовка будущих инженеров, как одна из со- ставляющих их профессиональной компетентности, необходима, прежде всего, для того чтобы инженер, перед которым производство все время ставит практические и теоретические проблемы, мог научно
∙о б ъ я с н я т ь происходящие явления,
∙у п р а в л я т ь технологическими процессами,

§ 28. Исследование временных рядов средствами вейвлет-анализа 155
∙п р о г н о з и р о в а т ь их последствия.
Рациональное осмысление триединства целей науки [объяснение + управ- ление + прогноз] опирается, в конечном счете, на математическую модель динамического процесса, каковым является, например, вибрация сложных агрегатов (металлорежущих станков, буровых установок, мостов, геофлю- идных потоков, нефтегазопроводов и т.п.). В последнюю четверть века стало понятным, что окружающий нас мир
∙сильно нелинейный (для его описания используются нелинейные дифференциальные уравнения и нелинейные отображения)
∙турбулентный (нет лапласовского детерминизма, но есть детермини- рованный хаос)
∙иерархический (образно говоря, «в каждой матрешке лежит две или более подобных ей матрешек»; это немедленно привело к появлению фрактальной геометрии, изучающей самоподобные объекты и использую- щей новые методики вычисления — как правило, дробных — размерно- стей этих объектов).
Понятием самоподобия человечество владеет с тех пор, как люди ста- ли понимать красоту, гармонию. Еще Платон, которого, по словам Павла Флоренского, «равно чтили и христиане, и язычники» и которого «древние апологеты называли христианином до Христа», упоминал о самоподобии «сущего — зримого и безвидного», вкладывая в «Диалогах» в уста Сократа слова о том, что гармония несет в себе еще одну гармонию, а дисгармония не содержит никакой гармонии.
Фрактальная геометрия, собрав на начальной стадии своего развития
обширную коллекцию фракталов и мультифракталов и научившись их классифицировать, сегодня переходит к объяснению физических причин и следствий фрактальности в сложных системах — природных, технических, абстрактных. При этом еще более возросла роль методики определения фрактальных размерностей, так как теперь они уже являются параметрами конкретных физических моделей, что предъявляет особые требования к точности соответствующей методики.
Вибросигнал представляет собой некую функцию s = f (t) от времени
t. Как показывает практика, f (t) обладает тем или иным самоподобием. Это означает, что график самоподобной функции инвариантен относительно некоторого класса непрерывных преобразований плоскости (t, s) . Напри-
мер, одной из многих используемых модельных функций является функ-
ция Ван дер Вардена f (x) = å∞ |
ϕn (x) , где ϕn (x) = |
1 |
|arcsin sin 2n πx| , |
|||
π2n+1 |
||||||
|
n=0 |
|
|
|
||
nN. Она инвариантна относительно аффинных преобразований |
||||||
A : (x, y) a (1 x, 1 (x + y)), |
|
|
||||
2 |
2 |
|
|
|
||
B : (x, y) a (1 |
(x +1), |
1 (−x + y +1)) |
|
|
||
2 |
|
|
2 |
|
|
|

§ 28. Исследование временных рядов средствами вейвлет-анализа 157
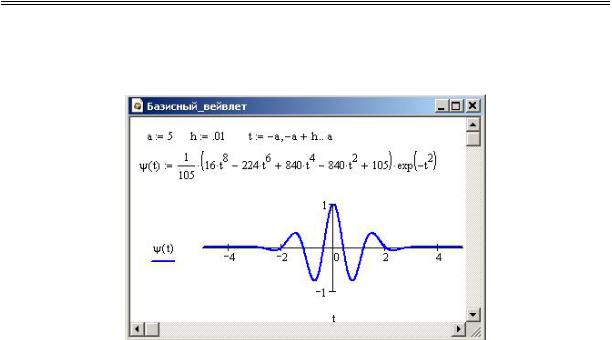
базисного вейвлета, позволяя полностью сконструировать пространство
L2(R).
Результатом преобразования (113) является поверхность W — дву-
Рис. 33. График базисного вейвлета ψ.
мерный набор коэффициентов (его визуализируют путем проектирования коэффициентов на плоскость ab и сопоставления величине коэффициентов некой цветовой гаммы), в котором, как и в коэффициентах преобразования Фурье, заключена информация о частотных характеристиках сигнала (бла- годаря параметру a). Более того, сохраняется информация и о поведении сигнала во времени (благодаря параметру b), что выгодно отличает вейв- лет-разложение от преобразования Фурье. Платой за это является некото- рое ухудшение разрешения по частоте, так как любой вейвлет, в отличие от синусоиды, в частотном пространстве не представляет собой δ- функции. Однако этот недостаток во многом компенсируется гладкостью набора вейвлет-коэффициентов, которая в Фурье-анализе достигается лишь применением искусственных операций. Полученные коэффициенты легко сопоставить с привычным спектром мощности. Для этого достаточно найти следующий интеграл [1]:
E(a) = òW 2 (a,b) d b. |
(114) |
Зависимость E(a) иногда называют скалограммой (рис. 34). Смысл энер-
гетического спектра ей придает тот факт, что для вейвлет-преобразования существует аналог теоремы Парсеваля. Для того чтобы сопоставить спектр мощности и скалограмму, необходимо перейти от параметра а к частоте ω,
воспользовавшись соотношением
aω = ωψ , |
(115) |
где ωψ — это константа, зависящая от выбора базисного вейвлета. Проще
158 ГЛАВА 6. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ…
всего ее можно оценить, применив формулу (115) к скалограмме модель- ного сигнала с известными частотами.
Известно, что если функция f (t) самоаффинна, то есть остается ин-
вариантной при масштабировании вида
t a λt, f a λH f ,
то ее спектр мощности имеет степенной характер:
P(ω) ~ ω−2H −1. |
(116) |
Такое же соотношение, очевидно, справедливо и для скалограммы (114) [14, 15, 16], однако она представляет собой уже гораздо более гладкую
5000
Е
0
0 |
a |
1 |
Рис. 34. Скалограмма.
функцию. Это, впрочем, является не главным достоинством вейвлет- преобразования. Естественность использования вейвлетов при анализе фрактальных сигналов обусловлена иерархичностью вейвлетного базиса. Фрактальность подразумевает воспроизведение каких-либо характеристик сигнала на разных масштабах, а вейвлет-преобразование как бы произво-
дит иерархизацию особенностей сигнала в зависимости от их масштаба (частоты), с сохранением их пространственной (временной) локализации. В результате, самоподобие сигнала приводит к самоподобию картины его вейвлет-разложения. При этом разработаны различные (помимо скало- граммы) способы извлечения численных характеристик из такой самопо- добной картины. Так как набор вейвлет-коэффициентов несет в себе избы- точную информацию, то часто используют только самую информативную часть данных, а именно, локальные максимумы (вдоль параметра b, при заданном значении а). Картину локальных максимумов иногда называют скелетоном (рис. 32 в). Для определения фрактальной размерности D по скелетону пользуются тем фактом, что

§ 28. Исследование временных рядов средствами вейвлет-анализа 159
lim log N(a) |
= D , |
(117) |
a→0 log a−1 |
|
|
где N(a) — это количество локальных максимумов на масштабе a.
Для кривых Ван дер Вардена, как доказал профессор из Костромы С.Б. Ко-
зырев[17], D = 1.
Вкачестве еще одного преимущества вейвлет-преобразования перед преобразованием Фурье можно привести предсказуемость влияния гра- ничных эффектов, а именно, если базисный вейвлет имеет компактный но- ситель [–S; S], то на масштабе a влияние границы распространяется на рас- стояние aS. Область, внутри которой не происходит влияния граничных эффектов на величину вейвлет-коэффициентов, называют треугольником достоверности. Наличие такой области делает формулу (114) не совсем удобной для практических расчетов. Для устранения влияния граничных эффектов бывает удобно заменить интегрирование усреднением, которое позволяет учитывать только часть коэффициентов.
Формула (5) позволяет определять размерности монофракталов, одна- ко из вейвлет-разложения относительно легко можно извлечь любые муль- тифрактальные характеристики [14]. Кроме того, вейвлет-преобразование
(113)обобщается на многомерный случай [5], что позволяет анализировать двумерные наборы данных напрямую, не прибегая к анализу одномерных срезов.
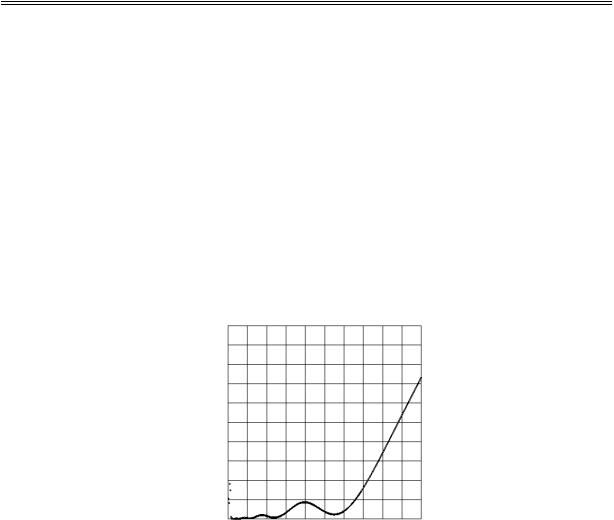
Вкачестве примера рассмотрим модельный временной ряд из 65 зна-
чений (табл. 60) для дискретного аргумента t [3, 4], взятого с шагом h = 1/64. [Функцию (118) К. Вейерштрасс предложил в качестве примера непрерыв- ной и всюду недифференцируемой функции.] Значения времени определяют-
ся по формуле: tn = 3 + n/64, n = 0 .. 64.
Т а б л и ц а 60
n |
X |
n |
X |
n |
X |
n |
X |
n |
X |
0 |
0 |
13 |
3,0505 |
26 |
3,3155 |
39 |
3,369 |
52 |
2,5433 |
1 |
0,7733 |
14 |
2,6724 |
27 |
3,4755 |
40 |
2,7386 |
53 |
3,0879 |
2 |
1,0156 |
15 |
2,58 |
28 |
2,7213 |
41 |
3,4879 |
54 |
2,704 |
3 |
1,5902 |
16 |
1,9065 |
29 |
3,0406 |
42 |
3,5459 |
55 |
2,5266 |
4 |
1,3209 |
17 |
2,7284 |
30 |
2,5023 |
43 |
3,8025 |
56 |
1,6669 |
5 |
2,1386 |
18 |
2,968 |
31 |
2,2819 |
44 |
3,1234 |
57 |
2,1972 |
6 |
2,0552 |
19 |
3,4905 |
32 |
1,5157 |
45 |
3,4905 |
58 |
2,0552 |
7 |
2,1973 |
20 |
3,1234 |
33 |
2,2817 |
46 |
2,9681 |
59 |
2,1388 |
8 |
1,6668 |
21 |
3,8024 |
34 |
2,5022 |
47 |
2,7286 |
60 |
1,321 |
9 |
2,5263 |
22 |
3,546 |
35 |
3,0406 |
48 |
1,9066 |
61 |
1,5902 |
10 |
2,7038 |
23 |
3,4881 |
36 |
2,7212 |
49 |
2,5798 |
62 |
1,0157 |
11 |
3,088 |
24 |
2,7387 |
37 |
3,4753 |
50 |
2,6723 |
63 |
0,7735 |
12 |
2,5433 |
25 |
3,3689 |
38 |
3,3155 |
51 |
3,0506 |
64 |
0 |
