v= Q ,	(4.7)
w
откуда Q=vw, м3/с [2, 3, 5,6, 10].
4.2. Уравнение неразрывности движения жидкости
Уравнение неразрывности для элементарной струйки и	потока

жидкости может быть получено путем следующих рассуждений. Если поток несжимаемой жидкости сплошной, то с течением времени изменения (увеличения или уменьшения) ее массы в данном объеме не произойдет. В потоке жидкость сплошь заполняет занимаемое ею пространство без образования пустот, т.е. движение жидкости происходит неразрывно и в этом случае справедливо уравнение неразрывности движения, выводимое на основе закона сохранения масс.

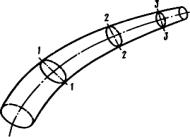
Получим уравнение неразрывности при установившемся движении жидкости для элементарной струйки (рис. 4.3). Возьмем сечение 1-1 с

площадью		w1	и скоростью		движения частиц жидкости и1.
Элементарный расход через сечение 1-1 равен							Q1 = u1 w1 .
	Затем возьмем сечение 2-2 в этой же струйке с площадью сечения w2 и
скоростью u1. Элементарный расход через сечение 2-2 равен Q2 = u2 w2 .
	По определению элементарной струйки приток и отток жидкости
через ее боковую поверхность невозможен;
на участке 1-2, который сохраняет
неизменные размеры, не образуется пустот и
не	происходит		переуплотнений;		значит
количества		жидкости,		протекающей		в
единицу времени через сечения 1-1 и 2-2,
должны быть одинаковы, т.е.					Q1 =	Q2 .
Принимая во внимание, что сечения 1-1 и 2-							Рис. 4.3. Движение жидкости в
2	приняты	произвольно,		можно	в общем		элементарной струйке тока
случае для элементарной струйки написать

Q1 =	Q2 =	Q3 = ... = Qn =	Q = const ,	(4.8)
		или
u1 w1 = u2	w2	= u3 w3 = ... = un	wn = Q = const .	(4.9)

Это уравнение неразрывности (сплошности) для элементарной струйки – элементарный расход жидкости Q при установившемся движении есть величина постоянная для всей элементарной струйки.

57

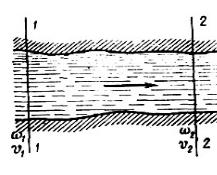
Взяв в потоке два произвольных сечения 1- 1 и 2-2 (рис. 4.4) и представив живые сечения их состоящими из суммы элементарных

струек, можно написать	Q1 = å u1 w1 – расход жидкости в сечении 1-1;
	w1

Q2 = å u2 w2 – расход жидкости в сечении 2-2.

w2

Скорости касательны к боковой поверхности потока и, следовательно,

вотсек между сечениями 1-1 и 2-2 через боковую поверхность движения жидкости не происходит; не изменяется и объем отсека. Следовательно,

вотсек через сечение 1-1 поступает столько же жидкости, сколько за то

же время выходит Q1 = Q2 . Так как сечения 1-1 и 2-2 взяты произвольно, то можно написать, что Q1 = Q2 = ... = Qn = Q = const или, выражая расход жидкости в сечениях через среднюю скорость v, получим

v1 w1 = v2 w2 = ... = vn wn

Это уравнение неразрывности для потока жидкости, расход жидкости через любое сечение потока при установившемся движении есть величина постоянная. Из уравнения

неразрывности для двух сечений можно вывести: v1 v2 = w2 w1 , т.е.

средние скорости потока обратно пропорциональны площадям соответствующих живых сечений [2, 10].

= Q = const .

(4.10)

Рис. 4.4. Движение жидкости в потоке

4.3. Уравнение Д. Бернулли

Уравнение Д. Бернулли для элементарной струйки невязкой и вязкой жидкости. Уравнение выведено Д. Бернулли в 1738г. для струйки идеальной несжимаемой жидкости постоянной плотности ρ , находящейся под действием только сил тяжести. Уравнение является основным уравнением гидродинамики и связывает (для установившегося течения) скорость текущей жидкости v, давление в ней р и высоту h расположения малого объёма жидкости над плоскостью отсчёта.

Выделим внутри жидкости бесконечно малую частицу в виде параллелепипеда (рис. 4.5). Рассмотрим уравнение движения частицы

58

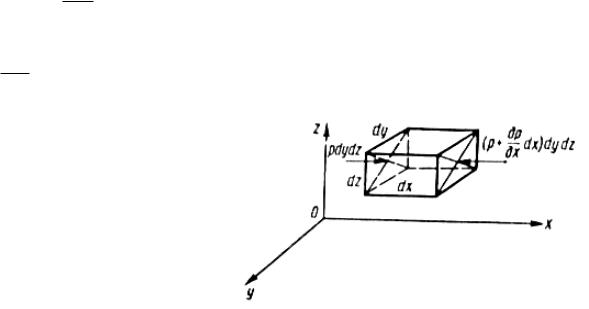
	жидкости	вдоль	оси 0–Х. На эту	частицу			будут	действовать	силы
				æ		¶ р	ö
	давления	слева	– ρdydz, справа –	ç	р +		dx÷ dydz	и массовая	сила
						¶ х
				è			ø

ρdxdydzX. Если к действующим на частицу движущейся жидкости силам добавить силы инерции с обратным знаком, то на основании постулата Даламбера можно рассматривать эту частицу как находящуюся в покое.

Составляющая сил инерции по координатной оси O-X будет равна: ρdxdydz dudtx . Эта же составляющая, отнесенная к единице массы, т.е.

деленная на ρdxdydz определяется по оси О-Х следующим значением: –1

dudtx .

Добавляя к уравнениям равновесия покоящейся жидкости силы инерции, получаем дифференциальные уравнения движения невязкой жидкости (уравнения Эйлера) в проекциях по направлению осей О-Х, О- Y, О-Z:

X −

1 ∂ p

=

dux

;

Рис. 4.5. Действие сил на движущуюся частицу

жидкости

ρ

∂ x

dt

Y −

1 ∂ p

=

duy

;

ρ

∂ y

dt

Z −

1 ∂ p

=

duz

.

ρ

∂ z

dt

Умножим слагаемые уравнений соответственно на dx, dy, dz и

сложим их:

( Xdx + Ydy +

Zdz) -

1

æ

¶ p

¶ p

¶ p

ö

du

duy

du

ç

dx +

dy +

dz ÷

=

x dx +

dy +

z

dz

. (4.11)

ρ

ç

¶ x

¶ y

¶ z

÷

dt

dt

dt

è

ø

Выражение Xdx + Y dy + Zdz – это полный дифференциал некоторой функции П, т.е.

59

dП=Xdx + Y dy + Zd,

(4.12)

считая движение установившимся и p=f(x, у, z) можно записать:

dp =

∂ p

dx +

∂ p

dy +

∂ p

dz .

(4.13)

∂ x

∂ y

∂ z

dx

dux

dux

æ

2

ö

Так как ux =

ç

ux

÷

, то

dx =

uxdt

= uxdux

= dç

÷ .

dt

dt

dt

2

è

ø

По аналогии с этим

du

y

æ

u 2

ö

dy =

ç

y

÷

и

dt

dç

2

÷

è

ø

duz

æ

2

ö

dz =

dç

uz

÷ .

(4.14)

dt

ç

2

÷

è

ø

Подставив полученные выражения в уравнение 4.11 получим

dП -

1

dp = 1 d (u2 ) ,

или

ρ

2

1

dp +

1 d(u 2 )

−

dП = 0 .

(4.15)

ρ

2

После интегрирования получим

p

+

u2

−

П =

const .

(4.16)

ρ

2

Если движение жидкости происходит только под действием внешней силы тяжести, то dП=Zdz=–gz , откуда П= –gz. Подставив это выражение в уравнение 4.16 получим:

	p	+	u2	+ gz = const ,	(4.17)
	ρ		2

60

или после деления на g получаем интеграл Бернулли:

	z +	p	+	u 2	= const = H ,	(4.18)
		γ		2g

где Н – гидродинамический напор, м.

Уравнение можно записать для двух сечений элементарной струйки 1-1 и 2-2 в виде равенства гидродинамических напоров в этих сечениях Н1=Н2:

z1 +	p	+	u2	= z2 +	p	2	+	u2
	1		1					2	.	(4.19)
	γ		2g		γ
								2g

Выражение называется уравнением Бернулли для элементарной

струйки невязкой жидкости.

Для реальной (вязкой) жидкости напор в любом вышележащем сечении всегда будет больше напора в нижележащем по течению сечении, т.к. часть энергии затрачивается на преодоление сил сопротивления, т.е. можно записать уравнение Бернулли для элементарной струйки вязкой жидкости в следующем виде:

z1 +	p	+	u2	= z2 +	p	2	+	u2	+ hw ,
	1		1					2		(4.20)
	γ		2g		γ			2g

где hw=Н1 –Н2 – удельные потери напора на преодоление всех сопротивлений (преодоление сил вязкости и сил трения между жидкостью и стенкой).

Уравнение Д. Бернулли для потока вязкой жидкости. При переходе от элементарной струйки к потоку вязкой жидкости, имеющему конечные размеры, необходимо учесть неравномерность распределения скоростей в живых сечениях и иметь представление о случаях возможного и невозможного применения уравнения Бернулли.

Решение этих вопросов сводится к установлению поправочных коэффициентов и выделению потоков с плавно изменяющимся движением, т.е. таким движением, при котором угол расхождения между соседними элементарными струйками настолько мал, что составляющими скорости в поперечном сечении можно пренебречь. В этих условиях справедлив основной закон гидростатики, т. е. величина z+p/γ одинакова во всех точках сечения.

При движении вязкой жидкости вдоль твердой стенки ее скорость

61

достигает максимального значения в центральной части потока и уменьшается до нуля возле стенки. Неравномерное распределение скоростей означает неодинаковое скольжение одних элементарных струек по другим, движение вязкой жидкости сопровождается вращением частиц, вихреобразованием и перемешиванием. Поэтому, приходится вводить среднюю по сечению скорость v. Для приведения результатов расчетов по средней скорости в соответствие с действительными скоростями, вводится коэффициент Кориолиса α , характеризующий неравномерное распределение скоростей в живом сечении потока, представляющий собой отношение кинетической энергии, подсчитанной по истинным скоростям сечения, к той же энергии, вычисленной по средней скорости в этом же сечении потока

α = ò u3	dw	≈ 1+ 3ò (u − v)2	dw	,	(4.21)
	3		2
w	v w	w	v w

где u и v – соответственно истинная скорость и средняя местная скорость в любой точке живого сечения w. Обычно в трубопроводах и каналах α =1,05... 1,1, иногда приближенно принимают α = 1.

Поэтому для потока вязкой жидкости с учетом неравномерности распределения скоростей по живому сечению уравнение Бернулли запишется следующим образом:

p

α

v

2

p

2

α

v

2

z +

1

+

1

1 = z

2

+

+

2

2 + h

w

,

(4.22)

1

γ

2g

γ

2g

т.е. уравнение Бернулли устанавливает связь между высотными положениями частиц жидкости, давлением и скоростями в разных сечениях потока жидкости. Причем каждая из входящих в уравнение величин может изменяться, но сумма остается постоянной.

Физический смысл и графическая интерпретация уравнения Д. Бернулли. Для понимания физического смысла уравнения Бернулли все его слагаемые могут быть представлены графически (рис. 4.6). Для этого надо в выбранных сечениях установить пьезометры и скоростные трубки установить пьезометры и скоростные трубки.

Индексами (1) и (2) обозначены величины, соответственно относящиеся к живому сечению потока 1–1, взятому выше по течению, и к живому сечению 2–2, взятому ниже по течению. Все слагаемые, входящие в уравнение Бернулли, имеют линейную размерность и

62

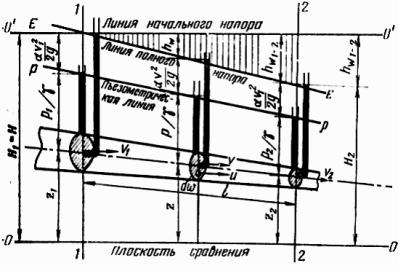
характеризуют собой высоту, z – геометрический напор или геометрическая высота положения центра тяжести живого сечения потока над произвольно взятой горизонтальной плоскостью сравнения 0–0; р/γ – высота давления, пьезометрический напор или пьезометрическая высота, т.е. высота такого столба жидкости, который соответствует гидродинамическому давлению в центре тяжести живого сечения потока; α v2/(2g) – скоростной напор или скоростная высота; α

– коэффициент неравномерности распределения скорости по сечению, при расчете трубопроводов α =1 и hw1-2 – потерянный напор.

Следовательно, сумма первых трех слагаемых уравнения Бернулли, обозначаемая через Н1 и Н2, имеет также размерность высот и называется полным гидродинамическим напором соответственно в сечениях 1–1 и 2–2. Член hw1-2 выражает суммарную потерю высоты (напора) между рассматриваемыми сечениями. Тогда уравнение Бернулли можно записать в следующем виде:

H1 = H2 + hw1− 2 = H ,

т. е. геометрический смысл уравнения Бернулли заключается в том, что при установившемся движении сумма четырех высот в каждом живом сечении потока есть величина постоянная и равна полной высоте – напору Н.

	z +	α v2			+		p	+ hw =	H
		(2g)					γ
	.		Если соединить
	уровни					жидкости			в
	пьезометрах,								то
	получим								Рис.4.6. Геометрическая интерпретация уравнения
	пьезометрическую
	линию.							Сумму Бернулли для потока жидкости
	æ		p ö
	ç z +			÷		называют			пьезометрическим (потенциальным) напором.
	ç	÷
	è		γ ø

Падение пьезометрической линии на единицу длины потока называют

пьезометрическим уклоном Iр, который выражают следующей зависимостью:

63

æ

p

ö

æ

p

2

ö

ç

z +

1

÷

-

ç

z

2

+

÷

ç

1

γ

÷

ç

γ

÷

,

(4.23)

I p =

è

ø

è

ø

l

где L – длина потока между сечениями 1–1 и 2–2.

Пьезометрический уклон может быть как положительным, так и отрицательным. Если соединить уровни жидкости в скоростных трубках, то получим линию полного напора. Падение линии полного напора на единицу длины называют гидравлическим уклоном I и выражают зависимостью:

æ

p

α

v

2

ö

æ

p

2

α

v

2

ö

H

− H

hц

ç

z

1

+

1

+

1 1 ÷

-

ç

z

2

+

+

2

2 ÷

1

2

ç

γ

2g

÷

ç

γ

2g

÷

I =

=

. (4.24)

I

=

è

ø

è

ø

l

l

l

Линия полного напора всегда понижается, т.е. при движении реальной жидкости часть напора затрачивается на преодоление сил трения.

При равномерном прямолинейном движении жидкости линия полного напора будет параллельна пьезометрической линии и гидравлический уклон будет равен пьезометрическому Ip=I. Равномерное движение происходит под влиянием перепада пьезометрических напоров Н1 и Н2. Так как уклоны Iр и I совпадают, то уравнение Бернулли можно упростить до вида Н1 –Н2=hw. Это значит, что равномерное движение напорных потоков возможно за счет перепада давления p1–р2 вдоль потока и (или) за счет разности удельных энергий положения z1– z2. При этом потери энергии не зависят от направления равномерного напорного потока в пространстве, которое может быть любым: и по горизонтали, и вверх и вниз по вертикали, и наклонно под произвольным углом.

Для безнапорного потока в условиях постоянного давления окружающей среды равномерное прямолинейное движение является результатом действия составляющей силы тяжести в направлении движения. Следовательно, оно может происходить в поле сил тяжести только сверху вниз по течению за счет падения потенциальной энергии z1– z2. Чем больше эта величина, т.е. чем больше пьезометрический и гидравлический уклоны Iр = I, тем больше при прочих равных условиях скорость течения жидкости.

Для идеальной жидкости линия полного напора будет параллельна

64