2.8. Вычисление объема холма при помощи интегрирования

Округлые формы рельефа – холмы, вулканические конусы, терриконы, карстовые блюдца и воронки – часто имеют настолько правильные очертания, что их можно рассматривать как тела, образуемые вращением профиля формы вокруг её оси симметрии. При планировке территории для подсчета объема выемок и насыпей необходимо знать объемы срезаемых и засыпаемых форм рельефа. Объемы вулканических конусов дают представление о количестве продуктов извержений, объемы карстовых воронок – о количестве растворенного материала. Объёмы такого рода форм рельефа можно вычислять, воспользовавшись формулой для определения объемов тел вращения с помощью определенного интеграла. Вычислим этим способом объем холма, профиль которого можно аппроксимировать экспоненциальной функцией , где– высота вершины;m– логарифмический декремент, характеризующий крутизну склонов: чем склоны холма круче, темm больше. Воспользуемся фор­мулой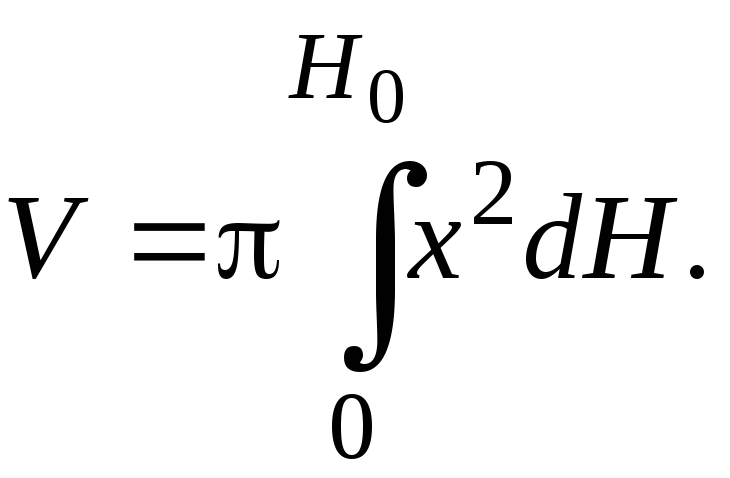Из равенствавыразим. Таким образом:

Подстановка верхнего предела интегрирования дает . При подстановке нижнего предела интегрирования используем то, что

;

(При вычислении данных пределов мы применили правило Лопиталя-Бернулли.) Поэтому при подстановке нижнего предела H= 0 выражение целиком обращается в нуль. Следовательно, объем холмаV =.

Пример. Вычислим объем холма, профиль которого можно аппроксимировать экспоненциальной функцией, где= 5м высота вершины;m = 0,35 – логарифмический декремент. Воспользуемся формулойV =. Подставляя значения, получаемV == 256,3 м².

2.9. Определение интенсивности потока фотонов [8, с. 39]

Определить в спектре Солнца интенсивность потока фотонов, которые могут приводить к разложению озона. Принять, что _max = 1180 нм — максимальная длина волны, способная разложить молекулу озона.

Интенсивность фотонов частоты  в верхних слоях атмосферы Земли вычисляется по модифицированной формуле Планка:

,

где  _E= 5,410 ⁶— среднее расстояние от Солнца до Земли,h,k,c — постоянные Планка, Больцмана и скорость света в вакууме,Т— абсолютная температура.

Проводя интегрирование по всем частотам от  _min=c/_max = = 2,510¹⁴ Гц до бесконечности и заменяяe^{h  / k T} – 1 наe^{h  / k T}, так как экспонента на много порядков больше единицы, получим интеграл:

.

Обозначая  a = h /k Tиb = 8 _E c ^– 2, имеем несобственный интеграл:

.

Несобственный интеграл по бесконечному промежутку понимают как предел:

.

Интеграл под знаком предела считают с помощью метода интегрирования по частям.

.

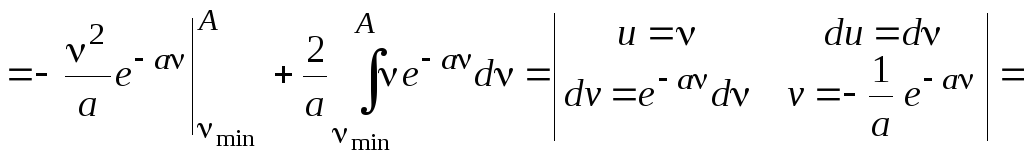
Переходя к пределу при  A  получим

фотоновсм^–2 с^–2.

3. Дифференциальные уравнения

Изменение природных процессов во времени может быть выражено с помощью математического аппарата в виде дифференциальных уравнений. Дифференциальные уравнения используются, например, в геоморфологии при изучении склоновых процессов, в динамической метеорологии. Особенно часто используются дифференциальные уравнения в геоморфологии, геологии и других областях, когда не удаётся установить непосредственную связь между переменными величинами и описать поведение системы в целом. Поэтому обычно выделяется часть системы и рассматривается её динамика в течение бесконечно малого промежутка времени, а также определяются зависимости, описывающие элементарный процесс. При этом приходится оперировать бесконечно малыми величинами и их отношениями, поэтому полученные зависимости будут включать переменные величины, их дифференциалы и производные, т.е. дифференциальные уравнения. Для перехода от бесконечно малых величин, которые связываются дифференциальными уравнениями, к конечным величинам, описывающим систему в целом, используется операция интегрирования.