Uchebno-metodicheskoe_posobie_Pravovaya_statistika

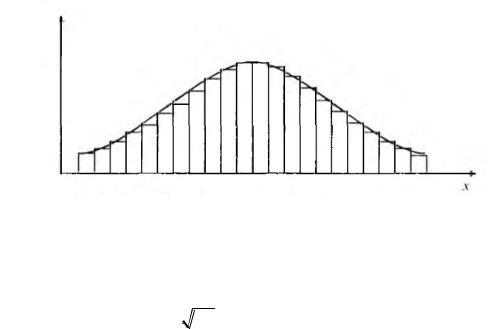
Рассматриваемые ранее случайные величины представляли собой некоторый ряд распределения, состоящий из вариантов и частот. Закономерность зависимости между вариантами и частотами графически может быть представлена в виде гистограммы (см. рис. 4.3).

Полученная кривая носит название кривой Гаусса и представляет собой математическую функцию, называемую нормальный закон распределения:

где y

x x

e

x x

t

1

2

		1					1	(	x x		)2
y
					e	2
			2					(4.13)

–ордината, или высота, кривой на любом расстоянии от х, т.е. от центра распределения, где х = 0. Вправо от центра распределения х имеет положительные значения, а влево – отрицательные;

–отклонение варианты от средней арифмети-

ческой величины (математического ожида-

ния) x = μ;

–среднее квадратическое отклонение, отражающее амплитуду колебания отдельных значений случайной величины от средней арифметической;

–математическая константа, равная отношению длины окружности к длине ее диаметра,

3,14159 ;

–основание натурального логарифма –

е= 2,71828;

–нормированное отклонение;

–максимальная ордината, соответствующая точке х по мере удаления от этой точки, т.е. от центра распределения, плотность значений случайной величины падает и кривая асимптотически приближается к оси абсцисс.

81

f (x)

Рис. 4.3. Кривая нормального распределения		x

Если принять, что = 1, то уравнение (4.13) примет следующий

вид:

		1				1	(	x x		)2
y
				e	2						(4.14)
		2

Кривая, описываемая этим уравнением, называется стандарти-

зованной кривой распределения Гаусса.

Согласно теории вероятности, случайная величина, распределенная по нормальному закону, практически всегда будет находиться от центра распределения в пределах ±3 , данное правило носит название «правила плюс-минус трех сигм». На основании соответствующих расчетов оно позволяет утверждать, что в пределах x ± 1 находится 68,28% всех вариант эмпирической совокупности, в пределах x ± 2 содержится 95,45%, а в пределах x ± 3 – 99,73% всех вариант совокупности.

В ряде случаев кривые распределения принимают асимметричный вид, со сдвигом максимума от средних значений вправо или влево (см. рис. 4.4), или имеют отклонения высоты максимума вверх или вниз от вершины кривой нормального распределения. Такой вид искажения называется эксцессом.

Асимметричность рассматриваемых распределений оценивается

коэффициентом асимметрии.

							As		3		(4.15)
									3
	где A							–	мера скошенности		распределения
			s						или коэффициент асимметрии;
				n
				(xi	x	)3 fi
		3		i 1				–	для сгруппированных данных.
				n

fi

i 1

82

Мо x		x Мо

Рис. 4.4. Правосторонняя и левосторонняя асимметрия распределения

Показатель эксцесса для сгруппированных данных вычисляется по формуле:

						Ex	4		(4.16)
							4
			n
где			(xi	x	)4 fi
	4	i 1				– центральный момент четвертого по-
			n
			fi			рядка.
			i 1

В случае эксцесса кривые распределения имеют отклонения высоты максимума вверх или вниз от вершины кривой нормального распределения (см. рис. 4.5).

Положительный островершинный

Нормальное

распределение

Отрицательный

плосковершинный

Х = 0

Рис. 4.5. Эксцесс распределения1

1 Рис. 4.3 – 4.5. См.: Правовая статистика: учебник / под ред. B.C. Лялина, А.В. Симоненко. 2-е изд., перераб. и доп. М.: ЮНИТИ-ДАНА, 2010.

83

Асимметрия и эксцесс позволяют определить однородность исследуемых социально-правовых явлений или процессов.

Биномиальное распределение.

Биномиальное распределение в теории вероятностей – распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна p.

Пусть x1, x2, x3,…, xn – конечная последовательность независимых случайных величин, имеющих одинаковое распределение Бернулли с параметром p, т.е. при каждом i=1, 2, 3,…, n величина xi принимает значения 1 («успех») и 0 («неудача») с вероятностями p и q=1 – p соответственно. Тогда случайная величина Y= x1+x2+x3+…+xn имеет биномиальное распределение с параметрами n и p. Это записывается в виде:

Y~B(n,p)

Функция вероятности представляется формулой:

								n
				pY	(k)						pk qn k , k 0,1, 2,..., n
								k
где n					n!				–		биномиальный коэффициент;
				(n k)!k!
k
						K! –					факториал числа k.

(4.17)

(4.18)

Функция распределения биномиального распределения может быть записана в виде:

y	n
FY ( y)			pk qn k , Y y и y R	(4.19)
k 1	k

При р = q = 0,5 (когда имеется одинаковое число объектов наблюдения с двумя противоположными признаками) распределение принимает строго симметричный вид.

В тех случаях, когда p q, биномиальное распределение принимает асимметричную форму. Чем больше разница между значениями р и q, тем больше степень асимметрии.

84

Распределение Пуассона

Распределение Пуассона наблюдается в том случае, если при большом числе наблюдений n появление некоторого события имеет исключительно малую вероятность р и при этом произведение nр также является небольшим числом.

Распределение Пуассона – вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что эти события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Выберем фиксированное число 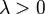и определим дискретное распределение, задаваемое следующей функцией вероятности:

p(k)	k
	e	(4.20)
	k !
Производящая функция моментов распределения Пуассона
имеет вид:
E (t) e (et 1)		(4.21)
Y

Следует отметить, что на практике при анализе социальноправовых задач чаще всего проводится исследование статистической совокупности достаточно однородных данных, которые подчиняются нормальному закону распределения.

2. Способы отбора, обеспечивающие репрезентативность выборки: повторная и бесповторная выборка

В зависимости от этого по охвату единиц обследуемой совокупности различают сплошное и несплошное наблюдение.

Сплошное наблюдение регистрируют все без исключения единицы наблюдаемой совокупности (N). Такое наблюдение называется

генеральной совокупностью.

Несплошное наблюдение позволяет изучить не всю генеральную совокупность, а лишь некоторую ее часть (n) – выборку (выборочную совокупность), подлежащую выборочному обследованию, при этом необходимо соблюсти определенные условия.

Выборочная совокупность позволяет: сократить сроки проведения исследования; сэкономить материальные и денежные затраты;

достижение большей точности результатов наблюдения (за счет сокращения количества ошибок регистрации).

Основная задача выборочного наблюдения состоит в том, чтобы характеристики показателей средней и доли выборки позволяли достоверно судить о средней и доле генеральной совокупности.

85

При этом следует учитывать закон больших чисел, сформулированный в начале XVIII столетия Я. Бернулли: «Чем больше объем выборочной совокупности будет приближаться к объему генеральной, тем точнее средняя выборочная будет воспроизводить среднюю генеральную величину».

Вдальнейшем академик П.Л. Чебышев доказал принципиальную возможность вычисления генеральной средней по данным слу-

чайной выборки (теорема Чебышева): «С вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе независимых наблюдений средняя величина изучаемого признака, полученная на основе выборки, будет сколь угодно мало отличаться от средней величины изучаемого признака по всей генеральной совокупности».

Всвою очередь, А.М. Ляпунов сформулировал теорему, позволяющую определить, с какой вероятностью могут возникнуть ошибки той или иной величины при данном числе наблюдений: «Независимо от вида распределения генеральной совокупности при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению».

Основные характеристики параметров генеральной и выборочной совокупностей представлены в табл. 4.6.

							Таблица 4.6
	Символы основных характеристик параметров
	генеральной и выборочной совокупностей
	Характеристика	Генеральная					Выборочная
		совокупность				совокупность
	Объем совокупности			N				n
	Количество единиц, обладающих данным		M					m
	признаком
	Доля единиц, обладающих данным призна-		p M				W m
	ком
				N				n
	Среднее значение признака			n				n
				xi				xi
			x	i 1			x	i 1
				N				n
	Дисперсия признака		n				n
			(xi		x)2		(xi x)2
		2 i 1				2	i 1
		x		N		x		n
	Среднее квадратическое отклонение призна-		n					n
	ка		(xi		x)2	x	(xi x)2
	x		i 1					i 1
	Дисперсия доли			N				n
			2	pq			2
			p			W W (1 W )
	Среднее квадратическое отклонение доли	p pq				W W (1 W )

86

Приведем пример нахождения характеристик параметров генеральной и выборочной совокупностей (см. табл. 4.7).

Таблица 4.7

Нахождение характеристик параметров генеральной и выборочной совокупностей

				Генеральная			Выборочная
				совокупность
							совокупность
	Характеристика			– Российская
							– Москва	2
				Федерация1
				(тыс.)			(тыс.)
		Исходные данные
Зарегистрировано преступлений за 2013 год –				2206249		174990
всего
в том числе:
особой тяжести				118617		9096
тяжких				419047		42831
средней тяжести				740159			56709
небольшой тяжести3				928426		66354
Объем совокупности				4		4
Количество	единиц, обладающих данным			1		1
признаком
Доля единиц, обладающих данным признаком				0,25		0,25
Среднее значение признака				551562		43747
Дисперсия признака				1,27532*1011		626873583
Среднее	квадратическое	отклонение		357117		25037
признака
Дисперсия доли				0,19		0,19
Среднее квадратическое отклонение доли				0,43		0,43

Следует отметить, что практически маловероятно значительное отклонение средней арифметической выборочной совокупности x от средней арифметической генеральной совокупности x , если число наблюдений достаточно велико.

P(		x x		) 1,	при n	(4.22)

По способу отбора единиц статистической совокупности различают следующие виды выборочного наблюдения:

1URL: http://crimestat.ru/offenses_chart.

2URL: http://crimestat.ru/regions_table_total.

3Для получения контрольной суммы добавлено два преступления.

87

собственно случайное; типическое (районированное); механическое; серийное (гнездовое).

Следует отметить, что при организации собственно случайного, типического и серийного выборочного наблюдения различают повторный и бесповторный отбор.

Повторный отбор – обследованная единица наблюдения или серия обязательно возвращается в генеральную совокупность и может подвергнуться повторному наблюдению.

Бесповторный отбор – обследованная единица не возвращается в генеральную совокупность и повторному наблюдению подвергнута быть не может.

Собственно случайная выборка предполагает отбор единиц наблюдения в случайном порядке методом жеребьевки.

После проведения отбора для определения возможных границ генеральных характеристик рассчитывается средняя и предельная ошибки выборки (см. табл. 4.8).

Таблица 4.8

Средняя ошибка репрезентативности собственно случайной выборки

Повторная выборка

Бесповторная выборка

Определение

среднего

2

2

n

размера

изучаемого

n

n (1

N )

признака

Определение

доли

W (1 W )

W (1 W )

(1

n

)

данного признака

n

n

N

Условные обозначения:

– средняя ошибка репрезентативности;

n

– численность выборки;

2

– показатель вариации (средний квадрат отклонений);

n

– доля выборки (обследованная часть совокупности);

N

1

n

– необследованная часть совокупности;

N

W

– доля данного признака в выборке;

(1 — W) – доля противоположного признака в выборке;

N

– численность генеральной совокупности.

Типическая (районированная) выборка – генеральная сово-

купность разбивается на однородные (типичные) группы, районы или зоны. При этом из каждой группы в случайном порядке выбирают установленное количество единиц наблюдения.

88

Распределение наблюдаемых единиц по группам производят пропорционально удельному весу каждой группы в общей генеральной совокупности. Предполагается, что каждая из групп является как бы самостоятельной (частной), но меньшей по размеру генеральной совокупностью.

Определение средней ошибки репрезентативности типической выборки представлено в табл. 4.9.

Таблица 4.9

Средняя ошибка репрезентативности типической выборки

Повторная выборка

Бесповторная выборка

Определение

среднего

2

2

n

размера

изучаемого

n

n (1 N )

признака

Определение

доли

W (1 W )

W (1 W )

(1

n

)

данного признака

n

s

N

Условные обозначения:

2

– средняя величина соответствующих показателей вариации по

отдельным группам;

W (1 W )

– средняя арифметическая взвешенная из произведений.

Механическая выборка, в отличие от типической, предполагает деление генеральной совокупности на равные по объему группы, число которых равно численности выборки, и при этом из каждой группы выбирают по одной единице наблюдения.

Механический отбор по сути представляет собой разновидность случайного отбора, и его точность не уступает собственно случайному отбору единиц наблюдения из генеральной совокупности.

Серийное (гнездовое) выборочное наблюдение применяется в тех случаях, когда организация собственно случайной, типической и механической выборки в соответствии с планом эксперимента нецелесообразна. Она предполагает, что отбору подлежат серии или группы единиц наблюдения, которые отбирают случайным или механическим способом. Затем в каждой отобранной серии производится сплошное наблюдение.

Серийная выборка дает менее точные результаты по сравнению с другими способами отбора, но в организационном отношении она гораздо проще.

Средняя ошибка репрезентативности серийной выборки с равновеликими сериями представлена в табл. 4.10.

89

Таблица 4.10

Средняя ошибка репрезентативности серийной выборки

Повторная выборка

Бесповторная выборка

Определение

среднего

s

2

s

2

s

размера

изучаемого

s

s

(1 S )

признака

Определение

доли

Ws (1 Ws )

Ws

(1 Ws )

(1

s

)

данного признака

s

s

S

Условные обозначения:

S – общее количество равных серий (групп) в генеральной совокупности; s – количество серий, отобранных для обследования в порядке случайной

повторной или бесповторной выборки;

s – показатель вариации изучаемого признака между сериями,

характеризующий возможные изменения серийных средних (межсерийный средний квадрат отклонений);

Ws – доля данного признака в среднем по всем обследованным группам (сериям).

Учитывая положения закона больших чисел, можно, изменяя объем выборки, регулировать пределы возможной ошибки репрезентативности.

При этом объем выборочного наблюдения зависит:

1) от показателей вариации наблюдаемого признака (чем больше показатели вариации ( 2 ) или W(1 – W), тем больше необходимая численность выборочной совокупности;

2) от размера предельной ошибки случайной выборки (чем меньше должен быть размер предельной ошибки, тем больше будет объем выборочного наблюдения, т.е. для получения большей точности необходимо увеличивать объем выборки);

3) от размера вероятности, с которой требуется гарантировать результаты выборки (чем выше показатель кратности ошибки t, тем больше должен быть объем выборки);

4) от способа отбора единиц выборочного наблюдения из генеральной совокупности (для бесповторного наблюдения, при прочих равных условиях, требуется меньшая численность выборки, чем при повторном отборе).

90