3.12. Жесткие задачи
Некоторые обыкновенные дифференциальные уравнения (ДУ) не решаются ни одним из рассмотренных методов. Чтобы понять, почему это так, рассмотрим структуру ДУ. В общем случае ДУ n-го порядка имеют n постоянных времени. Если одна из постоянных времени достаточно мала по сравнению с шагом интегрирования, то задача называется жесткой и ее трудно
решить обычными методами. В таких случаях шаг должен быть достаточно мал, чтобы можно было учитывать изменения наиболее быстроизменяющихся членов уравнения. В противном случае решение становится неустойчивым. Если величина шага очень мала по сравнению с интервалом, на котором отыскивается решение, то для получения решения потребуется очень много времени. А накапливающиеся в процессе длительных вычислений погрешности округления могут привести к получению бессмысленного результата. Рассмотрим, например, систему:
Если u(0) = v(0) =1, то решением будут (рис.3.7):
Рис. 3.7. Решение системы уравнений
После очень небольшого промежутка времени решение весьма близко к фун-кциям:
Предположим, что мы должны решить эту систему посредством метода Эйлера. Дискретное решение можно записать формулой:
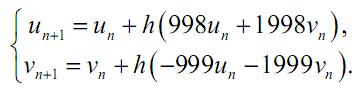
где u0= v0=1.
Если выбрать h = 0,02, то:
Рис.3.8. Семейство решений
Если сделать еще несколько шагов интегрирования, то результаты примут катастрофический характер. Это явление можно представить себе визуально, рассматривая семейство решений ассоциированных с u(t) (рис.3.8).
Переходная часть решения, которая, казалось бы, давно уже практически исчезла, тем не менее, мешает увеличить длину шага. Это особенно досадно, потому что на данном этапе вычислений решение очень гладко и, казалось бы, можно увеличить шаг.
Рис.3.9. Работа неявного метода Эйлера
Большинство стандартных методов не приспособлено для решения жестких уравнений. Поэтому были изобретены специальные методы. Простейшим из них является так называемый неявный метод
Эйлера, выражаемый формулой:
Работу неявного метода Эйлера покажем графически (рис.3.9).
Разработка эффективных методов для жестких уравнений является областью активных исследований.
назад
4.3. Динамическая модель технического объекта
Построение математической модели, какого либо объекта осуществляется на основе его динамической модели. Динамическая модель - это абстрактное графическое отображение основных физических свойств объекта и характеристик его взаимодействия с внешней средой [13].
При построении динамической модели следует принимать во внимание лишь те физические свойства объекта и воздействия внешней среды, которые могут оказать существенное влияние на точность результатов моделирования. Такой подход позволит избежать необоснованной избыточности в его математическом описании.
Структура динамической модели представляется в виде совокупности взаимодействующих элементов и её сложность зависит от степени абстрагирования при отображении физических свойств объекта. При построении динамических моделей используют следующие методы:
- методы сеток;
- метод функционально законченных элементов;
- метод сосредоточенных масс.
Методы сеток подразделяют на метод конечных разностей и метод конечных элементов. Они обычно используются при построении алгоритмической модели на микроуровне в системах с распределенными параметрами, описываемыми дифференциальными уравнениями в частных производных.
Метод функционально законченных элементов основан на выделении типовых элементов технического объекта, завершенных в конструктивном отношении и предназначенных для выполнения определенных функций (например, в гидромеханической системе - участок гидромагистрали, золотниковый клапан, дроссель, обратный клапан, насос, гидромотор и т. д.). Имея библиотеку математических моделей функционально законченных элементов и зная структуру технического объекта, можно составить полную математическую модель.
Наиболее часто при построении динамической модели используют метод сосредоточенных масс. Этот метод применим, если система имеет ярко выраженный дискретный спектр собственных частот. Это характерно для технических объектов, у которых масса распределена в пространстве неравномерно. Например, в механической системе автомобиля масса вращающихся деталей в основном сосредоточена в маховике двигателя, крупных шестернях трансмиссий, колесах, имеющих большие радиальные размеры и обладающих большими моментами инерции, а соединяющие их детали (валы, муфты, карданные передачи и др.) имеют малые радиальные размеры и массу, но обладают существенными упругими свойствами. Из названия метода следует, что он предназначен для моделирования объектов, мерой инертности элементов которых служит масса.
При построении динамической модели выделяют сосредоточенные массы, эквивалентные массам соответствующих частей объекта, и элементы, лишенные массы (невесомые), отображающие характер взаимодействия сосредоточенных масс.
Сосредоточенные
массы обладают инерционными свойствами
и способностью накапливать кинетическую
энергию. Их
называют инерционными элементами.
Взаимодействие
сосредоточенных масс осуществляя-ется
посредством упругих,
диссипативных,
фрик-ционных
и трансформаторных элементов.
Упругие элементы отображают упругие свойства динамической системы. Они обладают способностью накапливать потенциальную энергию.
Диссипативные элементы отображают свойство диссипации (рассеивания энергии) конструктивными элементами технического объекта, обусловленное силами внутреннего трения, пропорциональными относительной скорости перемещения взаимодействующих сосредоточенных масс (или сосредоточенных масс относительно внешней среды, например, при движении жидкости в трубопроводе).
Трансформаторные элементы отображают без инерционное преобразование параметров потока энергии, осуществляемое техническими устройствами, называемыми трансформаторами. Здесь речь идет о тех случаях, когда внутренними процессами трансформатора можно пренебречь и учитывать лишь пропорциональное изменение величины выходных переменных по отношению к величине переменных на его входе без преобразования вида энергии.
Пример
Используя метод сосредоточенных масс, построить динамическую модель для анализа плавности хода автомобиля (рис. 4.1) [13]. В связи с неровностями дороги, движение автомобиля сопровождается колебаниями кузова и вибрациями его механизмов и деталей. Для того чтобы создать нормальные условия водителю и комфортные условия пассажирам, применяют упругую подвеску автомобиля. Эта подвеска содержит упругие элементы и амортизаторы. Динамическая модель колебательной системы автомобиля имеет следующий вид. В этой модели учитывается масса части кузова m2, приходящаяся на колеса данного моста. Масса колес и моста m1.
Коэффициент сопротивления диссипативных элементов подвески m2 и шины m1. С учетом наложенных позиционных связей на сосредоточенные массы m1 и m2, они могут перемещаться только вертикально вдоль осей соответственно z1 и z2. Следовательно, система имеет две степени свободы.
Внешние воздействия на эту систему создаются неровностями микро- и макропрофиля дороги. Эти воздействия носят случайный характер и описываются случайными функциями q(t). Однако для более детального анализа влияния параметров подвески на колебания кузова необходимо учитывать связанность колебаний. В этом случае приходим к динамической модели плоских колебаний, в которой учитываются не только вертикальные колебания кузова относительно оси z0, но и угловые колебания b относительно оси y (рис.4.2).
Рис. 4.2. Динамическая модель плоских колебаний
Колебательная система имеет четыре степени свободы, и её состояние определяется фазовыми координатами z0, b2, z1, z2. Аналогичная модель используется при исследовании поперечных колебаний кузова.