5.3. Задача потребления.

Для иллюстрации применения результатов предыдущего пункта получим результаты, к которым пришёл Госсен, изучавший задачу потребления.

Пусть потребляются некие блага в количестве х_i i = 1, ..., n. Общая полезность i-го блага задана функцией Ти_i, функция полезности имеет вид:

и(х_i, ..., х_n) = Тu₁(х₁) + ... + Ти_n(х_n),

а предельная полезность — Ми_i = (см. п. 3.4). Предположим, что возможности потребления ограничены только временем Т. Пусть время t_i тратится на добывание блага х_i. Такое ограничение имеет вид:

t₁х₁ + ... + t_nх_n= Т.

Требуется вслед за Госсеном найти набор благ х_i, который соответствует максимуму функции и при имеющемся ограничении. Используем принцип Лагранжа для решения этой задачи. В этой задаче только одно ограничение g(x₁, ..., х_n) = t₁х₁ + ... + t_nx_n -Т, поэтому вводится единственный множитель Лагранжа λ. Составим функцию Лагранжа:

L(x, λ) = и(х) — λg(х) = Ти₁(х₁) + ... + Ти_n(х_n) — λ(t₁х₁ + ... + t_nx_n— Т).

Запишем уравнения Лагранжа:

5.12

I=1, 2, …, n.

t₁x₁+…+t_nx_n=T

Решение полученной системы уравнений — набор благ с максимальной полезностью.

Из этой системы следует, что для всех i, т.е. отношение предельной полезности блага к времени добывания этого блага — постоянная величина равная множителю Лагранжа.

Рассмотрим числовой пример. Пусть имеется 4 блага, функции Ти_i(х_i) = , а время Т = 9. В табл. 5.3 приведены значения k_i и t_i. Тогда из уравнений Лагранжа:

, i=1,…,4.

Отсюда

и λ=6

Остальные результаты расчёта приведены в

табл. 5.4. Максимально возможная полезность равна 27.

Таблица 5.3 Таблица 5.4

i	1	2	3	4
хi	0,75	3	0,75	0,75
Тиi(хi)	2,25	18	4,5	2,25

i	l	2	8	4
ki	4	2	8	4
ti	1	2	2	1

Условия Куна-Таккера.

В предыдущей лекции рассматривались ограничения g(x) = 0, т.е. ограничения в виде равенств. Некоторые экономические проблемы сводятся к задачам, в которых имеются ограничения другого вида, например, неравенства x₀ ≥ 0, x₁ ≥ 0, ..., x_n≥ 0 и g(x) ≤ b.

Рассмотрим геометрическую интерпретацию ограничений вида х ≥ 0. Они определяют n-мерный положительный ортант. Ортант — одна из 2ⁿ областей, на которые n-мерное пространство делится n взаимно перпендикулярными координатными гиперплоскостями. Неравенство g(х)≤b определяет подмножество этого ортанта.

Если решение задачи лежит на границе области, задаваемой ограничениями, то методом Лагранжа его найти нельзя. Для решения таких задач используются другие средства, например, теорема Куна-Таккера. Рас- смотрим её формулировку.

Пусть требуется найти максимум целевой функции и = и(x) при ограничениях g(x) ≤ b, x ≥ 0. Ограничения типа неравенства можно преобразовать в равенства. Для этого рассмотрим вектор s=b-g(x)=(s₁,..., s_m). Тогда задача формулируется так:

и = и(х) → max, g(x) + s = b и х ≥ 0, s ≥ 0

Составим функцию Лагранжа:

Пусть (x₀, х₁, ..., х _n, ₁, ..., _m) = (х, 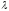) — стационарная точка, тогда в ней выполняются условия Ку на-Таккера:

5.12

5.13

5.14

5.15

5.16

5.17

Поскольку выполнены неравенства (5.12) и (5.14) в

уравнении (5.13) либо , либо х^*=0, либо эти равенства выполнены одновременно. Аналогично, в силу неравенств (5.15) и (5.17) из уравнения (5.16) следует, что либо , либо λ^* = 0, либо эти равенства выполнены одновременно. Запишем эти условия подробно:

.

Из этих равенств и неравенств (5.14) и (5.17) следует другая формулировка условий Куна-Таккера:

, если , j = 0, …., n

, если i = 1,….,m

g_i(x^*)=b, если i = 1,….,m

, если g(x^*)<b, i = 1,….,m

Условия Куна-Таккера в виде (5.18) называются условиями дополняющей нежесткости.

Рассмотрим пример. Пусть решается задача:

u(x₁, x ₂)= -4

x₁+x₂≤2

0.125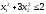

x₁≥0; x₂≥0

Составим функцию Лагранжа:

Условия Куна-Таккера:

-8x₁+6x₂-25-λ₁-0,25 λ₂x₁ ≤ 0

-10x₂+6x₁+40- λ₁-6 λ₂x₂ ≤ 0

(-8x₁+6x₂-25- λ₁-0,25 λ₂x₁)x₁+(-10x₂+6x₁+40- λ₁-6 λ₂x₂)x₂ = 0

x₁ ≥ 0, x₂ ≥ 0

2-x₁-x₂ ≥ 0

2 - 0,125- 3 ≥ 0

λ₁(2 – x₁ – x₂) + λ₂(2 - 0,125 - 3)=0

λ₁ ≥ 0; λ₂ ≥ 0

На рис. 5.5 заштриховано множество, удовлетворяющее ограничениям задачи. Целевая функция вогну- та, её первое пересечение с множеством — точка А координатами (0, 1). Она является решением задачи. Другие граничные точки множества В 0 (0, 0) и С (2, 0) не удовлетворяют всем условиям Куна-Таккера.

Условия Куна-Такке ра полностью характеризу- ют решение, однако в прак- тических проблемах часто они не дают аналитического решения. Поэтому алгорит- мы решения таких задач используют численные ме-тоды.

Приложения: