
- •Передмова
- •Програма курсу (і семестр)
- •І. Довідковий матеріал та методичні вказівки до розв’язування задач
- •1. Елементи лінійної алгебри.
- •2. Векторна алгебра та аналітична геометрія.
- •Правила диференціювання (правила знаходження похідних).
- •4. Дослідження функції за допомогою похідної.
- •5. Невизначений інтеграл
- •6. Визначений інтеграл
- •7. Диференціальне числення функції багатьох змінних
- •1. Вступ до математичного аналізу функції декількох змінних
- •2. Похідні та диференціали функції кількох змінних
- •Зауваження:
- •3.Повний приріст та повний диференціал функції
- •8. Диференціальні рівняння першого порядку
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •3. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •Розв’язання
- •9.Числові ряди
- •1. Загальні поняття
- •Розв’язання
- •2. Достатні ознаки збіжності знакододатних числових рядів Порівняльні ознаки
- •Розв’язання
- •Розв’язання
- •Розв’язання.
- •Розв’язання
- •3. Знакозмінні числові ряди
- •Поняття абсолютної та умовної збіжності ряду.
- •Розв’язання
- •Властивості збіжних рядів
- •Ііі. Функціональні ряди
- •1. Функціональні ряди, загальні поняття
- •2. Степеневі ряди
- •3. Область збіжності та властивості степеневих рядів
- •Розв’язання
- •Властивості степеневих рядів
- •Іі. Завдання для контрольної роботи
- •Література
І. Довідковий матеріал та методичні вказівки до розв’язування задач
1. Елементи лінійної алгебри.
Визначником квадратної матриці другого порядку

називається число, яке знаходиться за наступним правилом:
![]() . (1)
. (1)
Визначником квадратної матриці третього порядку

називається число, яке знаходиться за наступним правилом:
 (2)
(2)
Для обчислення визначників зручно користуватися наступною їх властивістю: визначник дорівнює сумі добутків елементів деякого рядка (стовпця) на їх алгебраїчні доповнення:
 (3)
(3)
В даному випадку визначник розкладено за елементами першого рядка.
Приклад 1. Обчислити визначник
 .
.
Розв’язання. По формулі (3) знаходимо:
![]()
Квадратна матриця виду

називається
одиничною.
Легко переконатися, що
![]() і
і
![]()
Матриця
![]() називається оберненою
по відношенню до матриці
називається оберненою
по відношенню до матриці
![]() ,
якщо
,
якщо
![]() .
.
Має
місце теорема
існування і єдиності оберненої матриці:
Обернена матриця
![]() існує (і єдина) тоді і тільки тоді, коли
існує (і єдина) тоді і тільки тоді, коли
![]() .
.
Для
обчислення оберненої матриці
![]() обчислюють
алгебраїчні доповнення елементів
матриці
обчислюють
алгебраїчні доповнення елементів
матриці
![]() ,
тоді
,
тоді
![]()
 . (4)
. (4)
Нехай дано систему лінійних алгебраїчних рівнянь
 (5)
(5)
Головним визначником даної системи називається визначник, складений із коефіцієнтів при невідомих
 . (6)
. (6)
Якщо
![]() ,
то система має єдиний розв’язок, який
може бути знайдено за правилом Крамера:
,
то система має єдиний розв’язок, який
може бути знайдено за правилом Крамера:
![]()
![]()
![]() (7)
(7)
Тут
 ,
,
 ,
,
 .
.
В матричній формі система рівнянь (5) має вигляд:
![]() (8)
(8)
де
 ,
,
 ,
,
 .
.
Розв’язок цієї системи
![]() . (9)
. (9)
Приклад 2. Розв’язати систему лінійних алгебраїчних рівнянь

а) за правилом Крамера; б) методом матричного числення.
Розв’язання.
Головний визначник системи
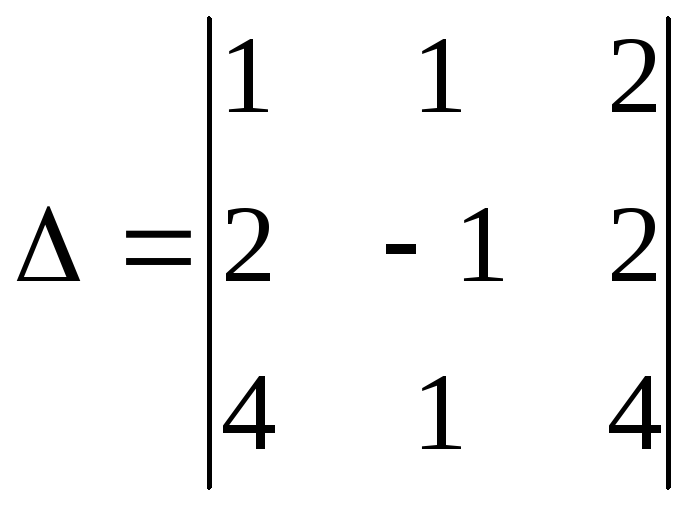
 .
.
Оскільки 0, то система має єдиний розв'язок. Далі обчислюємо
 ;
;
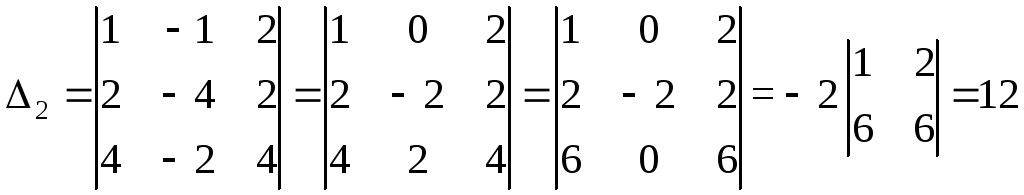 ;
;
 .
.
За формулами Крамера дістанемо:
![]()
В
матричній формі дана система рівнянь
має вигляд
![]() де
де
 ,
,
 ,
,
 .
.
Розв’язок
системи
![]() .
.
Для
знаходження оберненої матриці обчислюємо
алгебраїчні доповнення елементів
матриці
![]() :
:
![]()

Тоді обернена матриця
 ,
,
а розв’язок системи рівнянь

Таким
чином,
![]()
2. Векторна алгебра та аналітична геометрія.
Нехай
дано вектори
![]() Тоді операції над векторами здійснюються
за правилами:
Тоді операції над векторами здійснюються
за правилами:
1.
Модуль вектора
![]() . (13)
. (13)
2.
Сума (різниця) векторів
![]() . (14)
. (14)
3.
Скалярний добуток
![]() ,
де
,
де
![]() - кут між векторами;
- кут між векторами;
![]() . (15)
. (15)
4.
Векторний добуток
 . (16)
. (16)
5.
Мішаний добуток
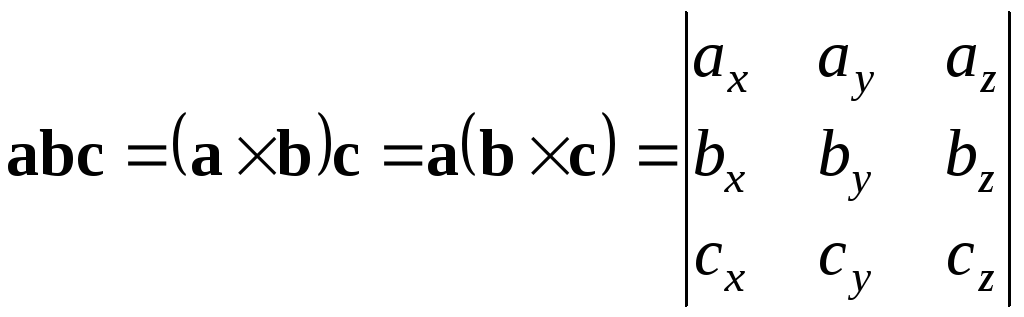 . (17)
. (17)
Косинус
кута
![]() між двома векторами
між двома векторами
![]() і
і
![]() знаходиться
за формулою
знаходиться
за формулою
![]() . (18)
. (18)
Проекція
вектора
![]() на напрямок вектора
на напрямок вектора
![]() дорівнює
дорівнює
![]() . (19)
. (19)
Умова перпендикулярності двох векторів: два ненулевих вектори взаємно перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.
Геометричний зміст модуля векторного добутку: модуль векторного добутку двох векторів чисельно дорівнює площі паралелограма, побудованого на цих векторах як на сторонах.
Геометричний зміст модуля мішаного добутку: модуль мішаного добутку трьох векторів чисельно дорівнює об’єму паралелепіпеда, побудованого на векторах як на ребрах.
Нормальним
вектором
площини називається будь-який вектор
![]() ,
який перпендикулярний до даної площини.
,
який перпендикулярний до даної площини.
Рівняння
площини, яка проходить через задану
точку
![]() перпендикулярно до вектора
перпендикулярно до вектора
![]() ,
має вигляд
,
має вигляд
![]() . (20) Загальне
рівняння
площини
. (20) Загальне
рівняння
площини
![]() . (21)
. (21)
Напрямним вектором прямої називається будь-який вектор, який лежить наданій прямій або на паралельній прямій.
Канонічні
рівняння прямої, яка проходить через
задану точку
![]() паралельно заданому вектору
паралельно заданому вектору
![]() мають вигляд
мають вигляд
![]() . (22)
. (22)
Умова паралельності двох площин має вигляд
![]() ; (23)
; (23)
умова перпендикулярності двох площин
![]() ; (24)
; (24)
умова паралельності двох прямих
![]() ; (25)
; (25)
умова перпендикулярності двох прямих
![]() ; (26)
; (26)
умова паралельності прямої і площини
![]() ; (27)
; (27)
умова перпендикулярності прямої і площини
![]() .
(28)
.
(28)
Приклад1. Дано координати чотирьох точок А1(2; 0; -3), А2(3; -2; 1), А3(4; 2; 1), А4(0; 2; -1). Скласти канонічні рівняння прямої, що проходить через точку А4 перпендикулярно до площини, що проходить через точки А1, А2, А3.
Розв’язання. В площині трикутника А1А2А3 побудуємо вектори (рис. 1)
A1A2={1; -2; 4}, A1A3={2; 2; 4},
Нормальний вектор цієї площини (який є напрямним вектором шуканої прямої)


Рис. 1
Отже, шукані канонічні рівняння прямої мають вигляд
![]() .
.
3. Похідна.
Нехай
дано функцію
![]() .Різниця
.Різниця
![]() називається приростом
аргумента x
в точці x0.
Аналогічно, різниця
називається приростом
аргумента x
в точці x0.
Аналогічно, різниця
![]() називається приростом
функції
називається приростом
функції
![]() в точці x0.
в точці x0.
Границя
відношення приросту функції до приросту
аргумента, коли приріст аргумента прямує
до нуля, називається похідною
функції в даній точці
![]() :
:
![]()
![]() .
.
Для знаходження похідних звичайно використовують таблицю основних похідних та правила диференціювання.
