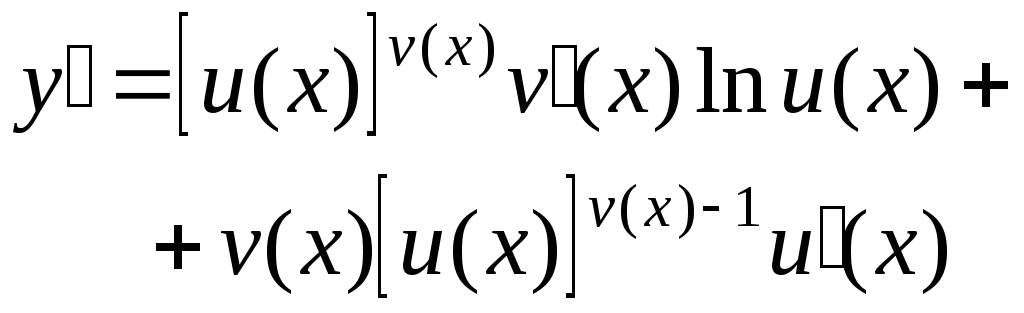Правила диференціювання (правила знаходження похідних).

№	Функція	Похідна
1
2
3
4	,
5
6

Приклад 2. Знайти похідну функції .

Розв’язання. Використовуючи правила диференціювання 1, 2 та формули 2, 7 із таблиці похідних, маємо:

.

Таблиця основних похідних.

№	Функція	Похідна
1
2
3
4
5
6
7
8
9
10
11
12
13
14

Приклад 3. Знайти похідну функції .

Розв’язання. Використовуючи правила диференціювання 3, 5 та формули 2, 13 із таблиці похідних, маємо: .

Приклад4. Знайти похідну функції

Розв’язання. Подано функцію як суперпозицію двох основних елемен-тарних функцій

де

Тоді за допомогою правила диференціювання складеної функції , де , що виражається формулою 5,

,

маємо

.

На практиці звичайно застосовують правило “ланцюжка”:

.

причому проміжні результати не записують,

.

Приклад 5. Знайти похідну функції .

Розв’язання. Логарифмуючи, дістанемо

.

Диференціюємо обидві частини останньої рівності:

.

Помножимо на y і підставимо замість y, тоді дістанемо

.

Зауваження. Такий же результат можна було б одержати, використавши формулу 6 із правил диференціювання.

Приклад 6. Знайти похідну функції .

Розв’язання. Подана функція задана неявно. Диференціюючи по x, дістанемо

,

звідки

,

і, остаточно,

.

Приклад 7. Знайти функції .

Розв’язання. Знаходимо першу похідну поданої функції:

.

Знаходимо другу похідну (як похідну від першої похідної):

4. Дослідження функції за допомогою похідної.

Необхідна умова зростання (спадання) функції. Якщо диференційовна в інтервалі функція зростає (спадає), то її похідна не може бути від’ємною (додатною) ні в одній точці даного інтервалу.

Достатня умова зростання (спадання) функції. Якщо неперервна на сегменті функція в кожній внутрішній точці цього сегменту має додатну (від’ємну) похідну, то ця функція зростає (спадає) на сегменті .

Функція має максимум (мінімум) в точці , якщо існує такий окіл точки , що для всіх точок , які належать цьому околу, виконується нерівність .

Необхідна ознака існування екстремуму функції. Якщо неперервна функція має в точці екстремум, то в цій точці похідна даної функції дорівнює нулю або не існує.

Точка , в якій похідна даної функції дорівнює нулю або не існує, називається критичною точкою.

Достатня ознака існування екстремуму функції. Якщо неперервна функція має похідну у всіх точках деякого інтервалу, який містить в собі критичну точку (за винятком, хіба що, самої цієї точки), і якщо похідна при переході аргумента з лівого боку в правий через критичну точку змінює знак з плюса на мінус, то функція в цій точці має максимум, а при зміні знака з мінуса на плюс – мінімум.

В деяких випадках при дослідженні функції на екстремум зручною виявляється наступна ознака існування екстремуму, яка використовує знак другої похідної. Нехай в точці перша похідна функції дорівнює нулю, а друга похідна існує і відмінна від нуля. Тоді, якщо , то в точці функція має максимум, а якщо , то в точці функція має мінімум.

Для заходження найбільшого і найменшого значень функції на сегменті потрібно: знайти всі критичні точки, які належать даному сегменту; обчислити в них, а також на кінцях сегмента, значення функції; із всіх цих значень вибрати найбільше та найменше.

Приклад9. Знайти найбільше і найменше значення функції на сегменті [0; 4].

Розв’язання. Знаходимо критичні точки функції на заданому сегменті. Для цього знаходимо похідну

.

Похідна дорівнює нулю в точках і . Сегменту належить тільки точка . Знаходимо: , , . Отже, найменше значення функції на даному сегменті дорівнює , а найбільше значення .