
- •Основные понятия и формулы
- •I. Векторная алгебра
- •Линейные операции над векторами
- •Линейная зависимость векторов. Геометрические критерии линейной зависимости
- •Базис и координаты
- •Ортонормированный базис. Декартова прямоугольная система координат
- •II. Аналитическая геометрия в пространстве Плоскость в пространстве
- •Прямая в пространстве
- •Прямая и плоскость в пространстве
- •III. Аналитическая геометрия на плоскости Прямая на плоскости
- •Кривые второго порядка
- •Парабола
- •Преобразования координат
- •IV. Поверхности второго порядка
- •620002, Екатеринбург, ул. Мира, 19
Кривые второго порядка
|
Эллипс |
|
|
|
Эллипс
- геометрическое место точек
|
![]() -
каноническое
уравнение эллипса.
-
каноническое
уравнение эллипса.
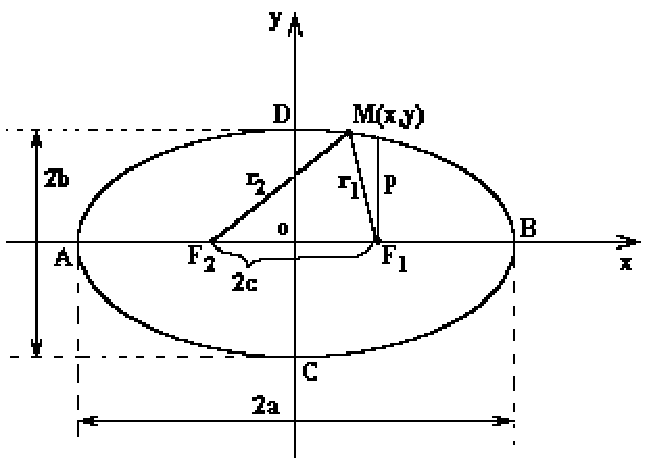
Эллипс
– центральная линия второго порядка,
замкнутая линия, симметричная относительно
осей и центра. Элементами эллипса
являются: точка О
- центр
эллипса; точки A,
B, C, D - вершины
эллипса; точки F1(с,0),
F2(-с,0)
- фокусы
эллипса; 2c
- фокусное
расстояние,
которое вычисляется по формуле
![]() ;
АВ=2а
и
CD=2b
- большая и малая оси эллипса;
a и b
- большая и
малая полуоси
эллипса;
;
АВ=2а
и
CD=2b
- большая и малая оси эллипса;
a и b
- большая и
малая полуоси
эллипса;
![]() -
эксцентриситет
эллипса, который вычисляется по формуле
-
эксцентриситет
эллипса, который вычисляется по формуле
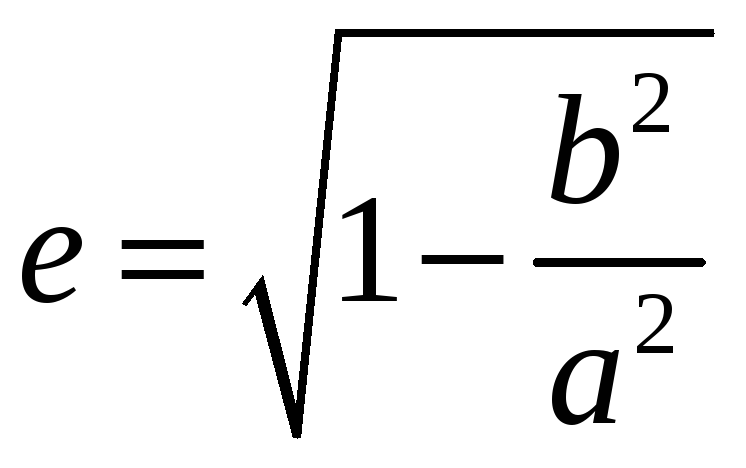 .
.
Эксцентриситет определяется отношением осей эллипса и характеризует его форму: чем больше e, тем более вытянут эллипс вдоль большой оси.
П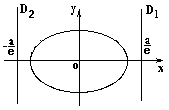 рямые
рямые
![]() и
и
![]() ,
параллельные малой оси эллипса и
отстоящие от его центра на расстояниях
,
параллельные малой оси эллипса и
отстоящие от его центра на расстояниях
![]() ,
называются директрисами
эллипса, соответствующими фокусам F1
и F2.
Отношение расстояния любой точки эллипса
до фокуса к расстоянию ее до соответствующей
директрисы постоянно и равно эксцентриситету
,
называются директрисами
эллипса, соответствующими фокусам F1
и F2.
Отношение расстояния любой точки эллипса
до фокуса к расстоянию ее до соответствующей
директрисы постоянно и равно эксцентриситету
![]() .
.
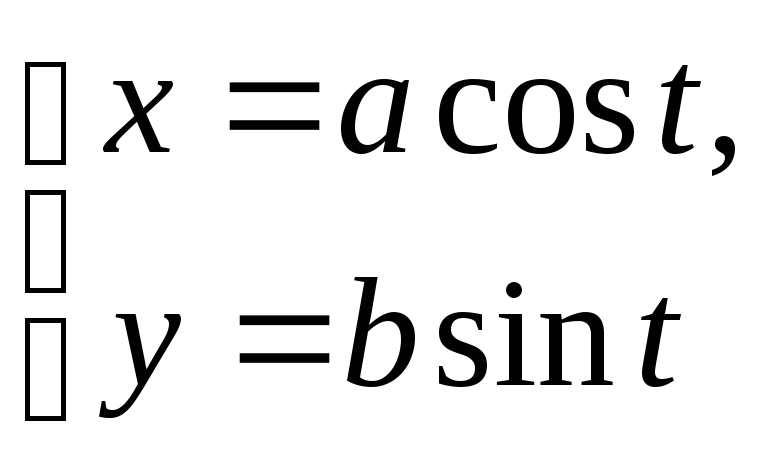 -
параметрические уравнения эллипса, где
t-параметр,
-
параметрические уравнения эллипса, где
t-параметр,
![]() ;
;
(t - угол, образованный подвижным радиусом с положительным направлением оси ox);
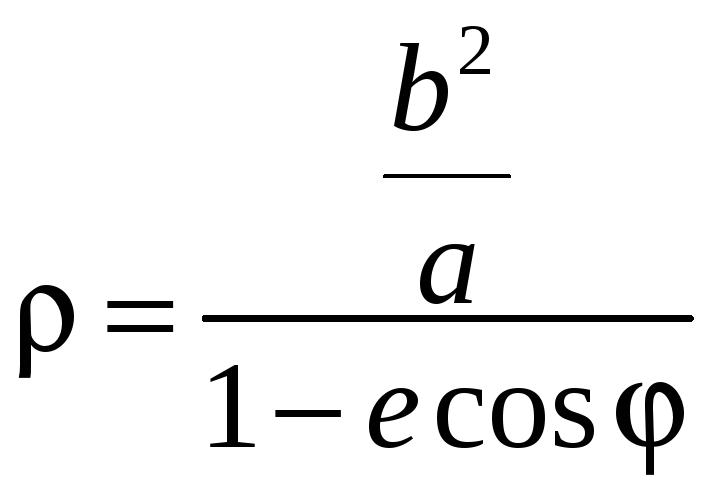 -
уравнение эллипса в полярных координатах,
связанных с фокусом,
-
уравнение эллипса в полярных координатах,
связанных с фокусом,
![]() -
эксцентриситет эллипса, если координатные
оси совпадают с осями эллипса.
-
эксцентриситет эллипса, если координатные
оси совпадают с осями эллипса.
|
Окружность |
|
||
|
|
Окружность - геометрическое место точек, равноудаленных от точки О (центр).
|
||
|
|
- параметрические уравнения окружности с радиусом R и центром в точке (x0,y0); |
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Гипербола |
|
||
|
|
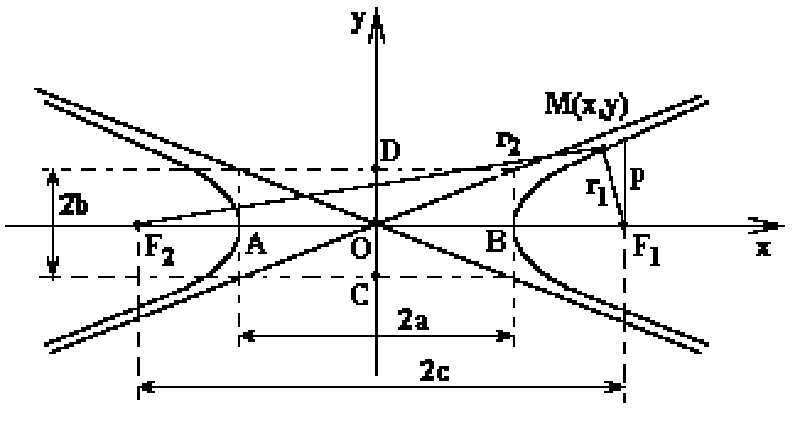
Гипербола
- геометрическое
место точек
Гипербола
– центральная линия второго порядка.
Она состоит из двух бесконечных ветвей,
симметрична относительно осей.
Элементами гиперболы являются: точка
О
- центр
гиперболы; точки А
и В
- вершины
гиперболы; точки F1(+ Эксцентриситет определяется отношением осей гиперболы и характеризует еe форму: чем больше e, тем более вытянут вдоль мнимой оси основной прямоугольник гиперболы. Асимптоты гиперболы - это прямые, к которым ветви гиперболы неограниченно приближаются при удалении в бесконечность.
Уравнения
асимптот гиперболы имеют вид
Угол
Сопряженные
гиперболы –
две гиперболы, которые в одной и той
же системе прямоугольных координат
при одних и тех же значениях
определяются
уравнениями
Сопряженные гиперболы имеют общие асимптоты. Действительная ось каждой из них есть мнимая ось другой и наоборот.
|
||
|
|
- параметрические уравнения одной ветви гиперболы; |
||
|
|
-
уравнение правой ветви гиперболы в
полярных координатах, связанных с
фокусом,
|
||

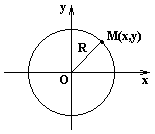
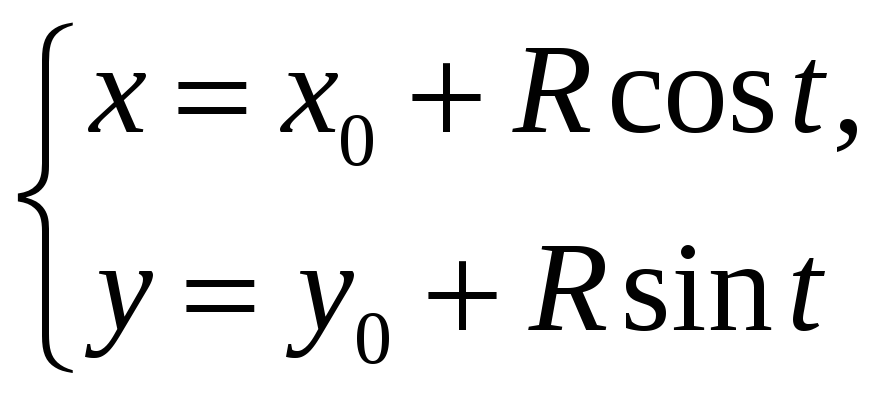
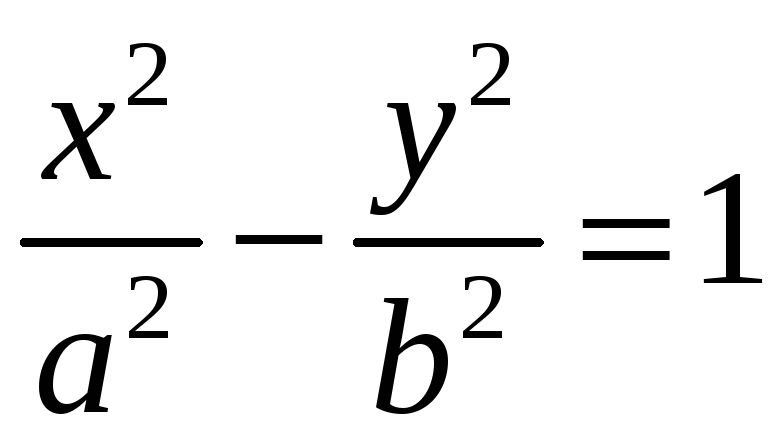 -
каноническое
уравнение гиперболы.
-
каноническое
уравнение гиперболы.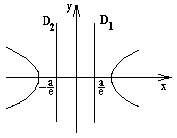 Прямые
Прямые
 и
и
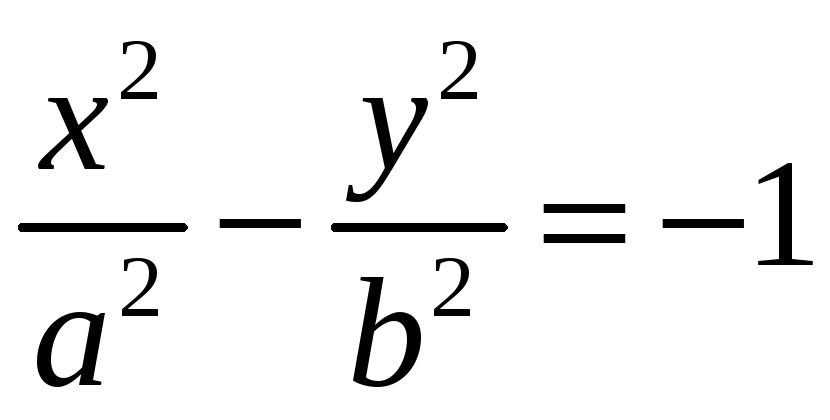 .
.
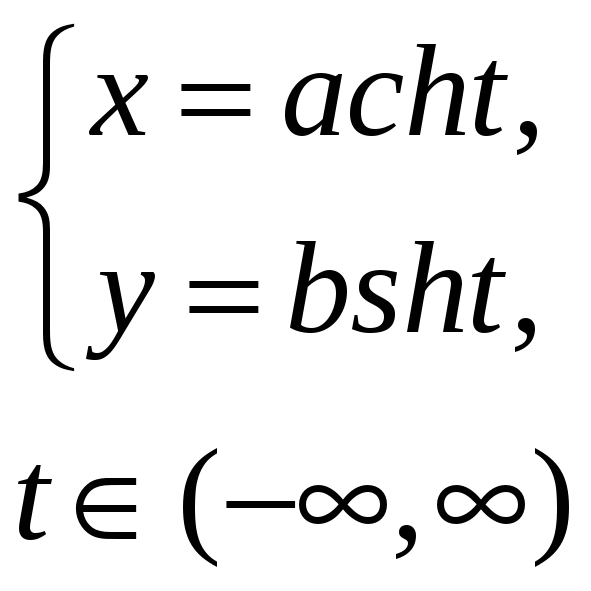

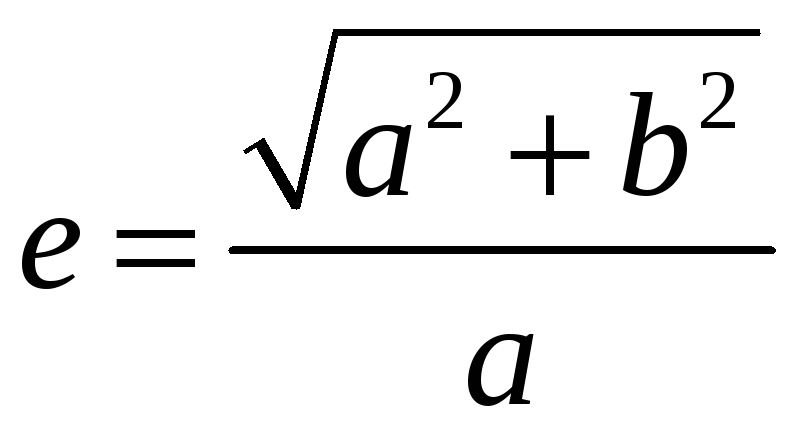 -
эксцентриситет гиперболы.
-
эксцентриситет гиперболы.