
- •Численные методы
- •Часть 3
- •Содержание
- •Введение
- •Классификация методов взвешенных невязок
- •Частные случаи метода взвешенных невязок
- •Метод моментов
- •Метод коллокаций
- •Метод подобластей
- •Метод наименьших квадратов
- •Метод конечных разностей
- •Расширение понятия функции
- •Пространство основных функций
- •Обобщенные функции
- •Дифференцирование обобщенных функций
- •Сходимость метода взвешенных невязок Основные понятия и определения
- •Обобщенное решение дифференциального уравнения
- •Сходимость метода конечных элементов
- •Контрольные вопросы и задания
- •Аппроксимация функций
- •Функции одной переменной
- •Кусочно-постоянные функции
- •Кусочно-линейные функции
- •Функции высших степеней
- •Иерархические многочлены
- •Функции двух переменных Треугольные конечные элементы. Линейная аппроксимация
- •Квадратичная аппроксимация
- •Четырехугольные конечные элементы
- •Функции трех переменных
- •Контрольные вопросы и задания
- •Задачи теплопроводности
- •Уравнение стационарной теплопроводности
- •Аппроксимация решения кусочно-линейными функциями
- •Процедура ансамблирования конечных элементов
- •Аппроксимация решения кусочно-квадратичными функциями
- •Использование иерархических многочленов
- •Уравнение нестационарной теплопроводности
- •Контрольные вопросы и задания
- •ЗадачИ механики деформируемого твердого тела Постановка задачи
- •Разрешающие соотношения метода взвешенных невязок Уравнение равновесия
- •Физические уравнения
- •Геометрические уравнения
- •Ансамблирование конечных элементов
- •Плоско-деформированное состояние
- •4 Узел 3 узел 3 узел
- •1 Элемент
- •2 Элемент
- •Плоско-напряженное состояние
- •Осесимметричное напряженно-деформированное состояние
- •Решение задач упругопластичности
- •Метод переменных параметров упругости
- •Метод дополнительных нагрузок
- •Контрольные вопросы и задания
- •ЗадачИ механики жидкости
- •Уравнения движения в переменных «функция тока – вихрь скорости»
- •Граничные условия
- •Граничные условия для функции тока
- •Граничные условия для функции завихренности
- •Соотношения метода взвешенных невязок
- •Разрешающие соотношения для функции тока
- •Разрешающие соотношения для функции завихренности
- •Разрешающие соотношения для поля давления
- •Алгоритм решения задачи
- •Контрольные вопросы и задания
- •Метод граничных элементов
- •Фундаментальное решение
- •Построение фундаментального решения
- •Контрольные вопросы и задания
- •Предметный указатель
- •Библиографический список
- •Приложение Бояршинов Михаил Геннадьевич Численные методы
- •Часть 3
-
ЗадачИ механики деформируемого твердого тела Постановка задачи
Пусть равновесное состояние тела (в рамках гипотезы о малых деформациях) описывается системой уравнений равновесия
![]() , (4.0)
, (4.0)
физических
![]() , (4.1)
, (4.1)
геометрических
![]() (4.2)
(4.2)
c силовыми
![]() (4.3)
(4.3)
и кинематическими граничными условиями
![]() . (4.4)
. (4.4)
Здесь обозначено:
![]() – оператор Гамильтона1;
– оператор Гамильтона1;
![]() – тензоры напряжений и малых деформаций;
– тензоры напряжений и малых деформаций;
![]() – вектор перемещений;
– вектор перемещений;
![]() – вектор внешней нормали к поверхности;
– вектор внешней нормали к поверхности;
![]() – векторы массовых и поверхностных
сил;
– векторы массовых и поверхностных
сил;
![]() – тензоры физико-механических свойств;
T – температурное поле;
– плотность материала. Вся поверхность
Г тела разделена на ГF
, где заданы поверхностные нагрузки, и
ГU, на которой заданы
кинематические граничные условия,
– тензоры физико-механических свойств;
T – температурное поле;
– плотность материала. Вся поверхность
Г тела разделена на ГF
, где заданы поверхностные нагрузки, и
ГU, на которой заданы
кинематические граничные условия,
![]() .
.
Разрешающие соотношения метода взвешенных невязок Уравнение равновесия
Поскольку уравнение ( 4 .0) векторное,
решением его является векторная функция,
а значит, для разложения его в ряд
необходимо построить систему векторных
пробных функций. Предположим, что
![]() – полная и замкнутая система скалярных
функций. Используя эту систему, построим
набор векторных пробных функций
– полная и замкнутая система скалярных
функций. Используя эту систему, построим
набор векторных пробных функций
![]() (4.5)
(4.5)
Пусть
![]() – приближенное решение уравнения ( 4 .0).
Взвесим невязки, получаемые при
подстановке этого решения в уравнение
( 4 .0) и граничное условие ( 4 .3), в соответствии
с идеей метода Галеркина, используя
систему векторных функций ( 4 .5),
– приближенное решение уравнения ( 4 .0).
Взвесим невязки, получаемые при
подстановке этого решения в уравнение
( 4 .0) и граничное условие ( 4 .3), в соответствии
с идеей метода Галеркина, используя
систему векторных функций ( 4 .5),
![]() , (4.6)
, (4.6)
![]() . (4.7)
. (4.7)
С помощью соотношений тензорного анализа [9]
![]() ,
,
![]()
и соотношения ( 4 .7) первое слагаемое выражения ( 4 .6) преобразуется к виду
![]()
![]() .
.
В результате выполненных преобразований получена ослабленная форма уравнения ( 4 .0)
![]() , (4.8)
, (4.8)
поскольку искомая функция
![]() теперь вынесена из-под знака производной.
Кроме этого, в выражение ( 4 .8) включены
силовые граничные условия ( 4 .3). Перейдем
от векторной формы записи к компонентной:
теперь вынесена из-под знака производной.
Кроме этого, в выражение ( 4 .8) включены
силовые граничные условия ( 4 .3). Перейдем
от векторной формы записи к компонентной:
![]() , (4.9)
, (4.9)
где компоненты метрического тензора [11]
![]()
В физических компонентах (обозначены чертой сверху) соотношение ( 4 .9) принимает вид
![]() . (4.10)
. (4.10)
В последнем выражении Hj, j = 1, 2, 3 – коэффициенты Ляме. В декартовой ортогональной системе координат H1 = H2 = H3 = 1. В этом случае выражение ( 4 .10) преобразуется к виду (далее знак черты над символами опущен)
![]() .
.
Для вектора
![]() это соотношение записывается в форме
это соотношение записывается в форме
![]()
![]()
![]()
 .
.
Учитывая, что согласно ( 4 .5)
![]() ,
предыдущее выражение приводится к виду
,
предыдущее выражение приводится к виду
 .
.
Аналогичные преобразования с использованием
![]() приводят к соотношениям
приводят к соотношениям
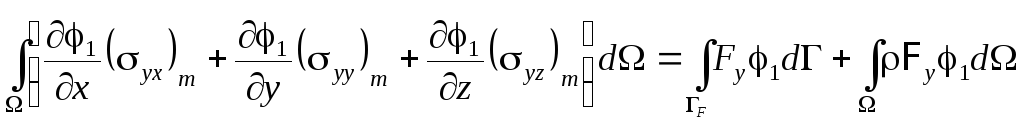 ,
,
 .
.
Для всей системы функций ( 4 .5) полученные выражения можно записать в виде
 (4.11)
(4.11)
где
![]() .
Вводятся матричные обозначения
.
Вводятся матричные обозначения
 ,
,
 ,
,
 , (4.12)
, (4.12)
с помощью которых систему уравнений ( 4 .11) можно записать в матричной форме
![]() . (4.13)
. (4.13)
Физические уравнения
Для упруго деформируемого тела связь между напряжениями и деформациями имеет вид закона Гука1
![]() , (4.14)
, (4.14)
где
![]() – объемная деформация;
и G – коэффициенты Ляме, которые
могут быть определены с помощью
коэффициента Пуассона
и модуля Юнга2
E,
– объемная деформация;
и G – коэффициенты Ляме, которые
могут быть определены с помощью
коэффициента Пуассона
и модуля Юнга2
E,
![]() .
.
Для рассматриваемого случая выражения ( 4 .14) принимают вид
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Полученные выражения могут быть записаны в матричной форме,
![]() ,
,
где
 .
.
Для учета возможных температурных деформаций за счет теплового расширения следует иметь в виду, что полная деформация определяется суммой
![]() ,
,
– коэффициент температурного расширения материала, T – температура, отсчитываемая от некоторого начального значения, объемная деформация определяется выражением
![]() .
.
В этом случае связь ( 4 .14) между упругими напряжениями и деформациями представляется в виде:
![]()
![]() .
.
Вводя обозначение
 ,
,
соотношения ( 4 .1) можно записать в матричном виде,
![]() . (4.15)
. (4.15)
