Алгоритм решения задачи

Вычисления начинаются в предположении, что в начальный момент времени функция завихренности  = 0 во всей области  . Решением системы уравнений ( 5 .11) определяется распределение функции тока  в той же области  . По найденному полю  с помощью формул ( 5 .1) вычисляются компоненты v_x и v_y вектора скорости. Это позволяет решить систему уравнений ( 5 .12) и определить функцию завихренности для следующего момента времени. После этого описанная процедура повторяется вновь. Вычисления продолжаются циклически до достижения требуемого момента времени. При необходимости нахождения стационарного решения задачи вычисления продолжаются, пока для двух последовательных моментов времени tⁿ и tⁿ⁺¹ выполняется условие

,

где  – малое положительное число; используется чебышевская норма, определенная на сеточной области. При найденных полях компонент v_x и v_y вектора скорости может быть найдено поле давления P с использованием разрешающих соотношений ( 5 .13).

Пример 5.1. Рассматривается течение вязкой жидкости в замкнутой полости (рис. 5 .1). Левая, нижняя и правая стенки полости неподвижны, верхняя крышка движется со скоростью V вправо. Требуется исследовать движение жидкости в полости.

Рис. 5.1. Схема течения жидкости

в замкнутой полости

Приближенные решения задачи разыскиваются в виде

,

,

где – линейные в пределах конечного элемента пробные функции. При вычислении элементов матриц встречаются интегралы вида

.

Для их вычисления таких интегралов с линейными пробными функциями _i удобно воспользоваться формулами [15]

,

где F_p – площадь p-го конечного элемента. С учетом¹ этого выражения получены матрицы

, ,

.

Рис. 5.2. Сетка конечных элементов, аппроксимирующая замкнутую полость.

На рис. 5 .2 показана сетка конечных элементов с нанесенными номерами узлов и треугольных элементов, аппроксимирующая замкнутую полость, занятую жидкостью.

На рис. 5 .3 представлены результаты вычисления функции тока  на сетках с увеличивающимся числом конечных элементов (структура сетки показана на рис. 5 .2), число Рейнольдса Re = 400, шаг интегрирования по времени t = 0,01. Результаты вычислительного эксперимента показывают, что уже при числе элементов, равном 512 и 2048, различие решений незначительно.

а б

в г

Рис. 5.3. Функции тока, полученные при расчетах на сетках с числом конечных элементов, равным 32 (а), 128 (б), 512 (в) и 2048 (г)

На рис. 5 .4 представлено поле функции завихренности , полученное при расчетах с использованием сетки из 2048 конечных элементов.

Рис. 5.4. Функции завихренности, полученные при расчетах на сетке с 2048 конечными элементами

Контрольные вопросы и задания

• Поясните физический смысл слагаемого 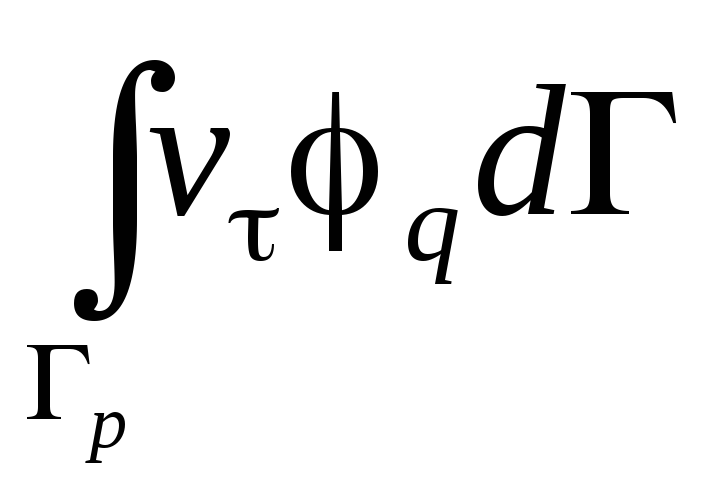, получающегося при выводе разрешающих соотношений для определения функции тока. Как повлияет его присутствие на выполнение процедуры ансамблирования конечных элементов?

• Установите вид матрицы в выражении ( 5 .11). Как выполнять вычисления этого слагаемого?

• Поясните физический смысл слагаемого , получающегося при выводе разрешающих соотношений для определения функции завихренности. Как повлияет его присутствие на выполнение процедуры ансамблирования конечных элементов?

• Установите вид матрицы в выражении ( 5 .12). Как выполнять вычисления этого слагаемого?

• При каких способах аппроксимации решений в пределах конечных элементов возможно нахождение поля давления P при использовании соотношений ( 5 .13)?