Геометрические уравнения

Вектор перемещений точек сплошной среды раскладывается по системе пробных функций,

. (4.16)

Установим матричную форму связи ( 4 .2) между компонентами тензора деформаций и компонентами вектора перемещений,

, , ,

,

, .

Полученные выражения в матричной записи

с помощью обозначений ( 4 .12) можно представить в форме

. (4.17)

Теперь, подставляя последовательно ( 4 .15) и ( 4 .17) в выражение ( 4 .13), получаем систему линейных алгебраических уравнений,

, (4.18)

относительно коэффициентов u_i, v_i и w_i разложения функции перемещения в ряд по пробным функциям ( 4 .5). Решение этой системы уравнений позволяет находить поля перемещений ( 4 .16), деформаций ( 4 .17), определять напряженное состояние тела, используя выражение ( 4 .15).

Ансамблирование конечных элементов

Пусть два конечных элемента имеют общую сторону (рис. 4 .0, а).

w_i w_i w_i

v_i v_i v_i

u_i F_z u_i u_i

F_y

F_x

а б

Рис. 4.0. Конечные элементы, имеющие общую сторону (а);

ансамблирование конечных элементов в единую композицию (б)

При объединении двух конечных элементов (рис. 4 .0, б) в единую композицию учитывается условие их механического взаимодействия¹. Это означает, что интегралы по поверхности Г_F в уравнениях ( 4 .18) для двух соседних элементов будут различаться лишь знаками. Поэтому при почленном сложении уравнений неизвестные усилия взаимодействия и (силы, являющиеся внутренними для системы этих элементов) будут исключены из уравнений. Коэффициенты, находящиеся при одинаковых узловых перемещениях (в рассматриваемом случае – u_i, v_i и w_i), будут складываться.

Для всего ансамбля конечных элементов, покрывающего исследуемую область, в результате ансамблирования все внутренние усилия будут исключены из результирующей системы линейных алгебраических уравнений. В конечном итоге в нее войдут лишь самые внешние поверхностные нагрузки, задаваемые граничными условиями вида ( 4 .3).

Плоско-деформированное состояние

В плоско-деформированном состоянии находятся тела, форма и размеры поперечного сечения, условия нагружения которых не зависят от одного из направлений. Размер тела в этом направлении велик, и продольной деформацией можно пренебречь. В качестве примера рассматривается длинный брус (рис. 4 .1, а), находящийся на твердой горизонтальной площадке под действием вертикальной нагрузки, не изменяющейся вдоль оси z. Форма и размеры его поперечного сечения вдоль этой же оси не изменяются.

y

y

x

Г Г_p



z 0 x

а б

Рис. 4.1. Схема плоско-деформированного состояния (а) и форма

поперечного сечения тела (б)

Для рассматриваемого случая, как показывают экспериментальные наблюдения, продольная деформация пренебрежимо мала, и можно считать, что . Кроме того, из анализа геометрических условий следует, что . С учетом этих допущений из соотношений закона Гука ( 4 .14) для упругого деформирования получаются выражения

, ,

, , , .

С другой стороны, из того же закона Гука следует

.

И, в силу ,

,

то есть компонента тензора напряжений не является независимой величиной. В этом случае матричное соотношение ( 4 .15) представляется в виде

, (4.19)

.

Учитывая, что , и решение задачи не зависит от переменной z, в системе разрешающих соотношений ( 4 .11) остаются лишь два уравнения

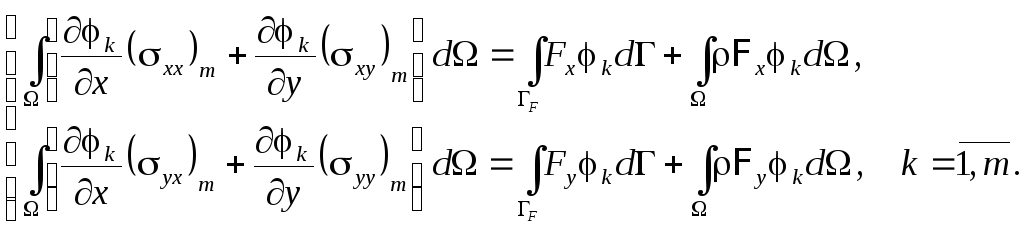
В матричной форме эти уравнения записываются в виде, аналогичном выражению ( 4 .13). Вид матрицы {_m} определен выражением ( 4 .19), а также используются обозначения

.

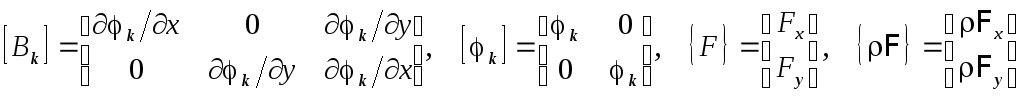Связь компонент тензора деформаций и вектора перемещений определяется в виде, аналогичном выражению ( 4 .17), где

.

С учетом введенных обозначений окончательно система алгебраических уравнений относительно искомых коэффициентов разложения имеет вид, аналогичный выражению ( 4 .18). Необходимо отметить, что при интегрировании по области  и границе Г,

,

,

причем во всех слагаемых системы уравнений ( 4 .18) появляется общий множитель L, равный размеру рассматриваемого тела в направлении оси z, который можно сократить. Иными словами, интегрирование в дальнейшем производится только по области _p поперечного сечения и по контуру _p границы (рис. 4 .1, б).

Пусть реализация разрешающих соотношений производится на треугольных конечных элементах с линейной интерполяцией решения внутри каждого из них,

где i, j, k – номера вершин произвольного конечного элемента, пробные функции _i, _j, _k определены выражениями (2.5). В матричной форме эти выражения представим в виде

.

Соответственно, матрицы [B_r], r = i, j, k имеют вид

, , ,

система уравнений ( 4 .18) преобразуется к форме

. (4.20)

Вычисляются значения матриц, входящих в эту систему уравнений:

,

,

,

,

,

,

,

,

;

;

;

.

При выводе этих выражений принято, что в пределах конечного элемента модуль упругости Е, температура T, коэффициенты Пуассона  и температурного расширения материала  постоянны; S_p – площадь p-го треугольного конечного элемента. Вводятся матричные обозначения

,

,

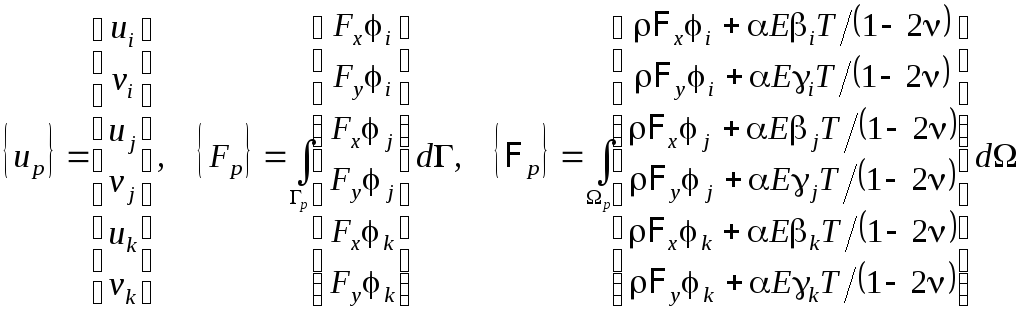где {u_p} – вектор всех узловых перемещений p-го треугольного конечного элемента, [K_p] – матрица жесткости для этого же конечного элемента. Теперь система уравнений ( 4 .20) для одного конечного элемента представляется в форме (суммирование по индексу p не производится)

.

Пример 4.1. Рассматривается осадка длинной стальной полосы с квадратным поперечным сечением размером 22 м², зажатой между двумя гладкими горизонтальными плитами (рис. 4 .2). Каждая из плит осаживается на величину . Требуется определить, на какую величину сместятся боковые стороны этой полосы в результате деформирования.

Так как форма поперечного сечения является симметричной, можно рассматривать лишь четверть исследуемой области (рис. 4 .2, б). Кинематические граничные условия указаны на том же рисунке. Поскольку плиты, деформирующие полосу, абсолютно гладкие, трение между ними и стальной полосой отсутствует, касательные усилия на контактной поверхности равны нулю. На свободной боковой поверхности полосы отсутствуют как нормальные, так и касательные нагрузки.

Для упрощения анализа алгоритма определения напряженно-деформированного состояния объекта рассматриваемая часть поперечного сечения полосы аппроксимируется только двумя конечными элементами, как это показано на рис. 4 .2, б.

y y 



x



0 x

а б

Рис. 4.2. Геометрическая схема осадки длинной полосы (а) и схема кинематических граничных условий (б)

Пробные функции для первого треугольного элемента, показанного на рис. 4 .3, определены в виде

.

y