Кусочно-линейные функции

Набор кусочно-линейных функций представлен на рис. 2 .2. Если все узлы отрезка [0, 1] перенумеровать, каждая функция будет ассоциироваться с i-м узлом, соответствующим ее номеру. В своем узле значение _i равно 1, а в соседних эта функция обращается в 0, изменяясь линейно вдоль прилежащих к этому узлу интервалов. Во всей остальной области пробная функция _i тождественно равна 0.

Как и в предыдущем случае, представим заданную функцию в виде разложения ( 2 .0) при m = 5, где

В соответствии с выражением ( 2 .1) определяются значения интегралов,

, ,

, .

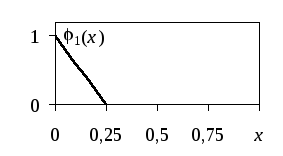
Рис. 2.2. Пробные кусочно-линейные функции

Вычисление остальных интегралов и подстановка полученных значений в выражение ( 2 .1) приводит к системе пяти линейных алгебраических уравнений относительно ,

(2.4)

Решением этой системы уравнений являются коэффициенты разложения

.

Нетрудно проверить, что найденные коэффициенты можно рассматривать в качестве приближенных значений аппроксимируемой функции в узлах сеточной области (рис. 2 .3).

Рис. 2.3. Аппроксимация зависимости (сплошная линия)

кусочно-линейными пробными функциями (–о–)

Из приведенных примеров следует, что при кусочно-постоянных функциях с каждым конечным интервалом [x_i, x_j] связана одна базисная функция _i(x) (рис. 2 .4, а), при кусочно-линейной аппроксимации с тем же интервалом ассоциируются две функции (рис. 2 .4, б),

и ,

где h = x_j – x_i – длина соответствующего интервала.

(x) _i(x) _j(x)

x_i x_j x_i x_j

а б

Рис. 2.4. Кусочно-постоянные (а) и кусочно-линейные (б) базисные функции, ассоциируемые с конечным отрезком [x_i, x_j]

Для второго примера ясен геометрический смысл коэффициентов разложения ( 2 .0) в ряд по базисным функциям

,

то есть коэффициент a_i аппроксимирует значение заданной функции в узле x_i разностной сетки. Этот факт широко используется в различных реализациях метода конечных элементов. Рассмотренный способ аппроксимации функций может быть продолжен для получения базисных функций более высоких порядков.

Функции высших степеней

Для построения квадратичной аппроксимации на отрезке [x_i, x_j] вводится дополнительный узел x_k (рис. 2.6), который, как правило, располагается в его центре. Первая функция конструируется в виде

.

Потребуем, чтобы она удовлетворяла на выбранном отрезке следующим условиям:

,

то есть в своем узле обращалась в 1, а в соседних была бы равна 0. Это требование приводит к системе трех линейных алгебраических уравнений

относительно коэффициентов ,  и . Определители этой системы

, ,

,

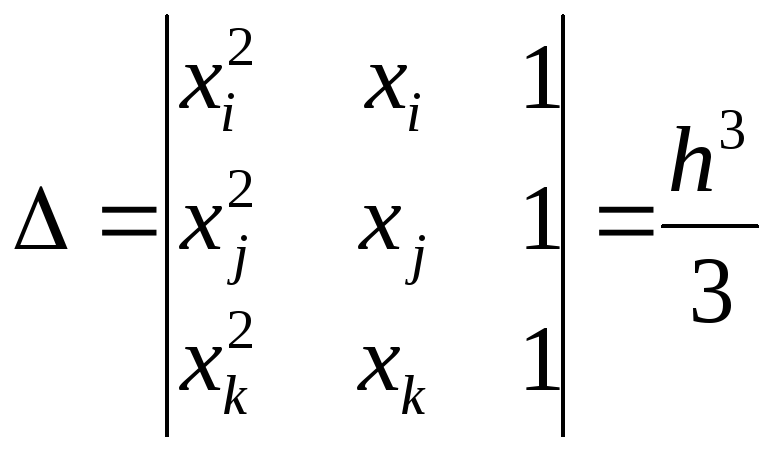позволяют вычислить и построить первую пробную функцию

.

Эта функция удовлетворяет всем предъявляемым требованиям. Аналогичным конструируются пробные функции

, .

Вид этих квадратичных функций, ассоциированных с отрезком [x_i, x_j], представлен на рис. 2.6. На рис. 2 .6 показаны те же функции, ассоциированные с узлами отрезка.

Рис. 2.5. Квадратичные пробные функции на отрезке [x_i, x_j]

В общем случае для построения на отрезке [x_i, x_j] системы базисных функций степени p

следует ввести дополнительно (p – 1) узлов. Коэффициенты , , ...,  могут быть определены из решения соответствующих систем линейных алгебраических уравнений

Вместе с тем целесообразно использовать для определения базисных функций способ, используемый при построении полинома Лагранжа,

.

Очевидно, что в этом случае

Кубические пробные функции, для построения которых внутри отрезка вводятся два дополнительных узла с координатами и , имеют вид

, ,

,

и показаны на рис. 2 .7.

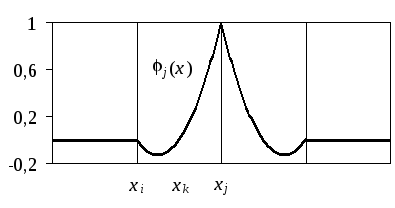
Рис. 2.6. Квадратичные пробные функции, ассоциируемые с узлами отрезка

Пусть на отрезке [x_i, x_j] задана естественная координата  с началом в центре отрезка,

.

Очевидно, что в пределах этого отрезка естественная координата принимает значения . В этой системе координат пробные функции представляются следующим образом:

– линейные

, ;

– квадратичные

, , ;

– кубические

, ,

, .

Рис. 2.7. Кубические пробные функции на отрезке [x_i, x_j]