7.5. Визначення положення центра ваги плоскої фігури за центрами ваги її частин. Спосіб від'ємних площ

Нехай, необхідно визначити положення центра ваги деякої плоскої фігури, яка складається з трьох частин, положення центрів ваги яких відомі (рис. 7.5).

Приймемо, що площі частин фігури відповідно F₁,F₂,F₃, a координати їх центрів ваги С₁,С₂,С₃ будуть x₁,y₁, x₂,y₂, x₃,y₃. Статичні моменти площі плоскої фігури відносно осей координат дорівнюють сумі статичних моментів площин окремих її частин, які можна визначити за (7.6):

Визначивши статичні моменти віднос­но осей координат, можна знайти ко­ординати її центра ваги за формулами (7.7):

Підставивши значення статичних моментів, одержимо

Рис. 7.5

^(7.8)

Цей спосіб зручно застосува­ти при визначенні центра ваги плос­кої фігури, з якої вирізана деяка час­тина (рис. 7.6).

Рис. 7.6

Знаючи площу F₁ всієї фігу­ри і координати х₁ і у₁ її центра ваги C₁, а також площу F₂ і координати х₂, у₂ центру ваги С₂ вирізаної з неї частини, можна визначити координати центра ваги частини фігури, що залишилася, за формулами, аналогічними (7.8). При цьому площа цієї частини повинна бути рівною різниці площ F₁ і F₂, а її статичні моменти - різниці їх статичних моментів. Тоді,

^(7.9)

Цей спосіб визначення центра ваги плоскої фігури, з якої вирі­зана деяка частина, називається способом від'ємних площ.

Аналогічний прийом, що називається способом від'ємних об'ємів, застосовується при визначенні координат центра ваги однорі­дного тіла, одержаного вирізом з тіла об'ємом V₁ і центром ваги C₁(x₁,y₁,z₁) частини об'ємом V₂ з центром ваги С₂(x₂,y₂,z₂).

Тоді

^(7.10)

7.6. Центр ваги лінії

Визначимо положення центрів ваги однорідних тіл, що мають велику довжину, при порівняно малій площі поперечного перерізу. Розглянемо, наприклад, кусок однорідного тонкого дроту постійного перерізу, вісь якого являє собою дугу АВ (рис. 7.7)

Рис. 7.7

Вагу дроту виразимо за формулою, де L - довжина лінії АВ, ρ - вага одиниці довжини дроту. Розіб'ємо лінію АВ на елементарні одиниці М_i довжиною . Вага кожної дільниці визна­чається за формулою . Координати центра ваги кожної дільниці позначимо x_i,y_i,z_i. Тоді координати центра ваги С для ко­жного куска дроту визначаються за формулами (7.3).

^;або

^{; аналогічно 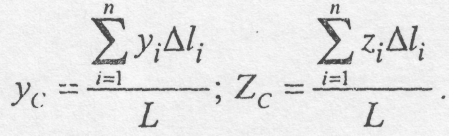(7.11)}

Переходячи до границі, при , будемо мати

(7.12)

де підсумовування розповсюджені на всі елементи дроту. Центр ваги однорідного тонкого дроту постійного перерізу, вісь якого співпадає з деякою лінією, називається центром ваги цієї лінії.

7.7. Центри ваги деяких ліній і плоских фігур

а) центр ваги площі трикутника

Розбиваючи площу трикутника на ряд стрічок, паралельних одній з сторін трикутника, переконуємось, що центри ваги всіх стрічок лежать на медіані трикутника (рис. 7.8):

Рис. 7.8

З цього випливає, що центр ваги С площини трикутника ле­жить на цій медіані, і, отже, на інших медіанах, тобто в точці перетину його медіан, що знаходиться на - висоти від кожної основи трикутника.

Рис. 7.9 Рис. 7.10

б) Центр ваги дуги кола

Візьмемо дугу АВ кола радіуса R з центральним кутом 2α (рис. 7.9). Оче­видно, що внаслідок симетрії фігури від­носно осі X, центр ваги буде лежати на осі X, тобто у_с = 0.Знайдемо ^{координату ус = 0. За формулою (6.12) маємо Згідно рис. 6.9}

Отже ^(7.13)

де α - половина центрального кута в радіанах. Наприклад, для дуги півкола будемо мати

в) Центр ваги кругового сектора

Нехай, дано круговий сектор. Роз­іб'ємо його на елементарні сектори. Кожний такий сектор можна прийняти за рівнобедрений трикутник висоти R. Висота у рівнобедреному трикутнику є одночасно і медіаною. Отже, центр ваги кожного елементарного трикут­ника буде лежати на дузі кола радіуса 2/3R.

Таким чином, центр ваги площі кругового сектора можна зна­ходити як центр ваги матеріальної лінії (дуги кола радіуса 2/3R), по якій неперервно розподілена вага цього сектора. Тому, застосовуючи формулу (7.13), одержимо координату центра ваги площі сектора.

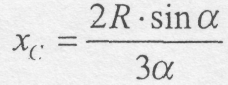^(7.14)

Для сектора півколаодержимо

г) експериментальний спосіб

Покажемо, як можна експериментально визначити одну з ко­ординат, - центра ваги літака (відстань а), якщо відстань АВ = l (рис. 7.11) відома. Поставивши колесо В на платформу ваги, зважуванням знайдемо силу тиску колеса на платформу; так само буде знайдена чисельно рівна цій силі реакція . Також зважуванням знаходимо реакцію . Прирівнюючи до нуля суму моментів всіх сил відносно центра ваги літака, одержуємо:

,звідки знаходимо

Рис. 7.11

Очевидно, , де Р — рівновага літака. Якщо значення величини Р наперед відомо, то для визначення а можна обійтись одним зважуванням.

Питання для самоконтролю

І.Що називають центром паралельних сил і які він має властивості ?

2.Як записується формула для радіуса-вектора і координат центра па­ралельних сил ?

З.За якими формулами визначаються координати центрів ваги одно­рідних тіл. плоских фігур і ліній?

4.Що називається статичним моментом площі плоскої фігури віднос­но осі, як він обчислюється та яку має розмірність?

5.Як визначити положення центра ваги плоскої фігури, якщо відомо положення центрів ваги окремих її частин ?

6.Напишіть формули для координат центра ваги дуги кола, і площі кругового сектора?

Задача 7.1

Знайти координати центра ваги площі поперечного перерізу нерівно­бокого кутника, розміри якого вказані на рис. 7.12:

Рис. 7.12

Розв'язок

Розіб'ємо кутник на два прямокутники, площі яких ; . На основі (7.8) формули для координат центра ваги кутника будуть: де x₁,y₁ - координати центра першого прямокутника, а x₂,y₂ - другого. Очевидно,

Таким чином, маємо

Задача 7.2

Знайти центр ваги пластинки радіуса R, в якій вирізаний отвір у ви­гляді прямокутника із сторонами а і b (рис.7.3).

Розв'язок

Пластинка симетрична відносно осі X; отже. Y_C = О. Залишається знайти лише координату x_с .

Рис. 7.13

Згідно (7.9) будемо мати

де

Таким чином.

Задача 7.3

Знайти граничну висоту h з конуса при якій тіло, що складається з конуса і півкулі однакової густини і однакового радіуса r, втратить стійкість в положенні рівноваги, коли вона спирається поверхнею півкулі на гладеньку горизонтальну площину (рис. 7.14):

Рис. 7.14

Розв'язок

Візьмемо початок координат в точці О. З умови задачі очевидно, що висота конуса повинна бути вибрана так, щоб центр ваги всього тіла не лежав вище точки О. Отже, граничну висоту конуса, при якій тіло втратить стійкість, ми знайдемо вважаючи, що центр ваги всього тіла збігається з точкою О. В силу симетрії тіла x_C=y_C=0 . Згідно (7.2) маємо , де - об'єм півкулі; h - об'єм конуса; z₁ = 3/8r - координати центра ваги півкулі; z₂ = 1/4h - координата центра ваги конуса. Так як центр ваги всього тіла повинен співпадати з точкою О, то Z_C = О і. отже: звідки