17. Условие параллельности и перпендикулярности прямых.

Угол между прямыми.

Пусть даны прямые

y

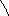
O x

Параллельность прямых.

Если и параллельны, то угол , .

Таким образом, можно сделать вывод, если прямые параллельны, то и наоборот.

Таким образом, равенство угловых коэффициентов является необходимым и достаточным условием параллельности двух прямых.

Перпендикулярность прямых.

Если прямые перпендикулярны, то .

При этом , .

Поэтому

Справедливо обратное утверждение.

Таким образом, для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.

Рассмотрим прямые, заданные общим уравнением прямой.

, .

Условие параллельности: .

Следовательно, условием параллельности прямых, заданных общим уравнением, является пропорциональность коэффициентов.

Условие перпендикулярности: .

.

Таким образом, условием перпендикулярности прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных x и y.

18. Расстояние от точки до прямой. Окружность и эллипс.

Точка пересечения прямых.

(1)

(2)

Очевидно, что пересечение их должно удовлетворять уравнению каждой прямой. Найдем пересечение из системы уравнений (1) и (2).

Если прямые не параллельны, т.е. , то решение дает единственную точку пересечения прямых.

Расстояние от точки до прямой.

Даны точка и прямая (3).

Под расстоянием от точки до прямой (1) понимается длина перпендикуляра , опущенного из точки на прямую (3).

Для определения расстояния от точки до прямой (3) необходимо найти прямую, перпендикулярную заданной и проходящую через точку . Допустим, что перпендикуляр пересекает исходную прямую в точке . Тогда расстояние от точки до прямой будет равна длине отрезка .

. Найдем значения и .

,

.

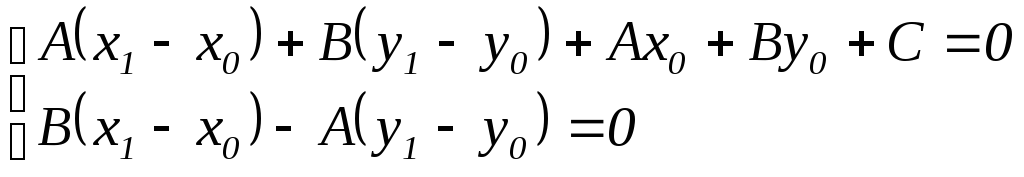
Окружность.

Определение. Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром окружности. Выведем уравнение окружности.

, (4)

где - центр окружности.

Формула (4) представляет собой каноническое (нормальное) уравнение окружности.

Если центр окружности совпадает с началом координат, то уравнение (4) примет вид:

Известно, что кривые второго порядка, каковой является и окружность, определяются уравнением вида:

,

где - некоторые действительные числа, называемые коэффициентами уравнения, причем по крайней мере один из коэффициентов A, B и C отличен от нуля.

В частности для окружности эти коэффициенты должны удовлетворять требованиям:

1. A = C.

2. B = 0.

3. .

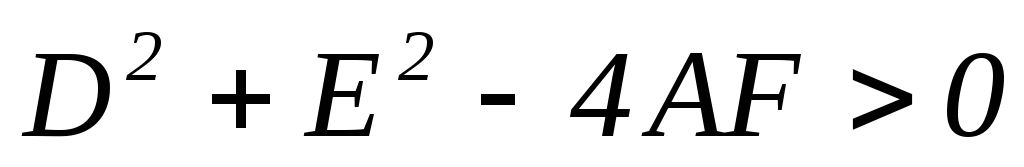Эллипс.

Определение. Эллипсом называется множество точек плоскости, сумма расстояний каждой из которых до двух данных точек и (называемых фокусами эллипса) есть величина постоянная, равная 2a.

П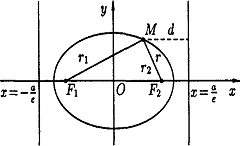усть М – произвольная точка эллипса с фокусами F₁ и F_2. Отрезки F₁М и F₂М (так же как и длины этих отрезков) называются фокальными радиусами точки М. Постоянную сумму фокальных радиусов точки эллипса принято обозначать через 2а. Таким образом, для любой точки М эллипса имеем:

F₁М + F₂М = 2а.

Расстояние F₁ и F₂ между фокусами обозначают через 2с. Пусть дан какой-нибудь эллипс с фокусами F₁, F_2.

Возьмем на плоскости произвольную точку М и обозначим ее координаты через х и у. Обозначим, далее, через r₁ и r₂ расстояния от точки М до фокусов (r₁ = F₁М, r₂ = F₂М). Точка М будет находиться на данном эллипсе в том и только в том случае, когда

r₁ + r₂ = 2а.

Чтобы получить искомое уравнение, нужно в равенстве заменить переменные r₁ и r₂ их выражениями через координаты х, у.

Заметим, что так как F₁ F₂ = 2с и так как фокусы F₁ и F₂ расположены на оси Ох симметрично относительно начала координат, то они имеют соответственно координаты (–с; 0) и (+с; 0); приняв это во внимание находим:

Заменяя r₁ и r₂, получаем:

Это и есть уравнение рассматриваемого эллипса, так как ему удовлетворяют координаты точки М(х; у), когда точка М лежит на этом эллипсе. Возведём обе части равенства в квадрат, получим:

или

Возводя в квадрат обе части последнего равенства, найдем:

а²х² — 2а²сх + а²с² + а²у² = а⁴ – 2а²сх + с²х², откуда (а² – с²)х² + а²у² = а²(а² – с²).

Здесь мы введем в рассмотрение новую величину ; а>с, следовательно, а²—с²>0 и величина b – вещественна.

b² = a² – c², тогда b²x² + a²y² = a²b² или .

Это уравнение называется каноническим уравнением эллипса.

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси; обозначив эксцентриситет буквой ε, получаем:

.