12. Решение невырожденных линейных систем. Формулы Крамера.

Как известно решение матричного уравнения записывается в виде: .

Согласно правилу умножения матриц имеем

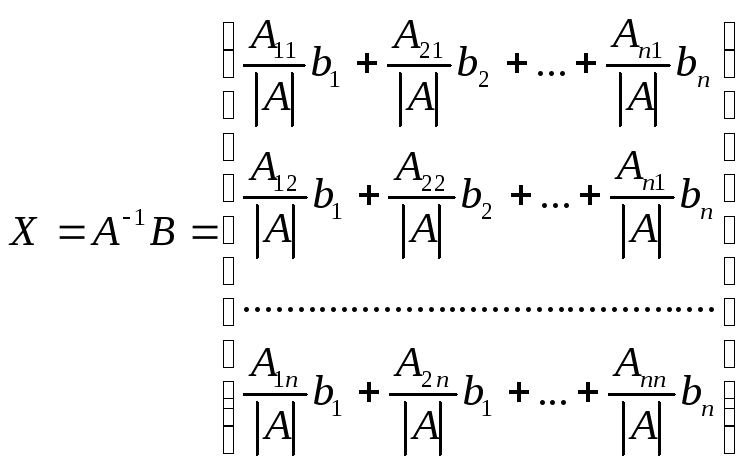
Отсюда , i = 1, 2, …, n.

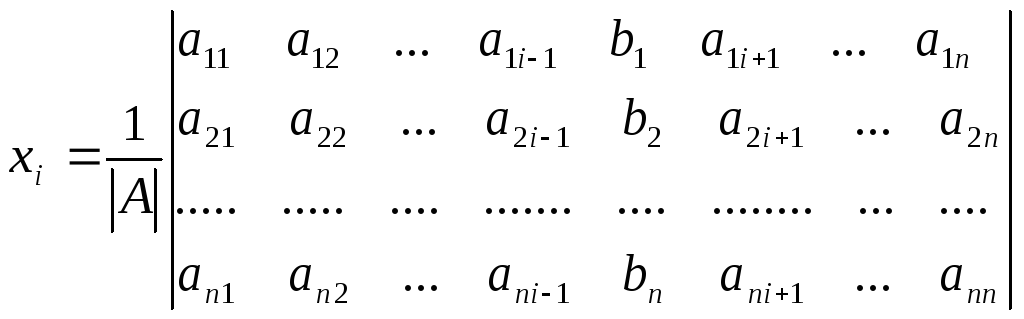
Запишем короче:

, i = 1, 2, …, n,

где – определитель системы; – определитель матрицы, получаемой из основной матрицы системы заменой её i-го столбца столбцом свободных членов.

Из самого способа решения ясно, что система имеет единственное решение.

Пример.

Система 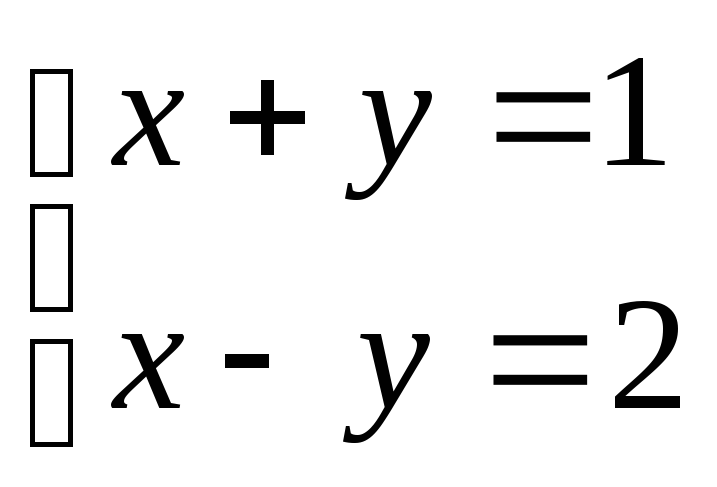имеет определитель отличный от нуля, поэтому имеет единственное решение, которое можно найти по формулам:

, , где , , т.е.

, .

13. Метод Гаусса. Система линейных однородных уравнений.

Пусть дана система линейных уравнений

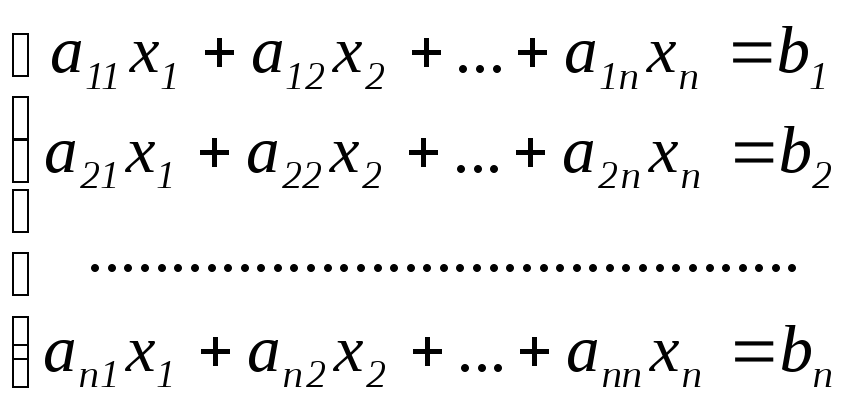(1)

Коэффициенты , считаются заданными.

Вектор-строка x₁ , x₂ , ... , x_n  - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.

Определитель n-го порядка a _ij , составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.

a) Если , то система (1) имеет единственное решение, которое может быть найдено методом Гаусса.

б) Если , то система (1) либо имеет бесконечное множество решений, либо несовместна, т.е. решений нет.

1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.

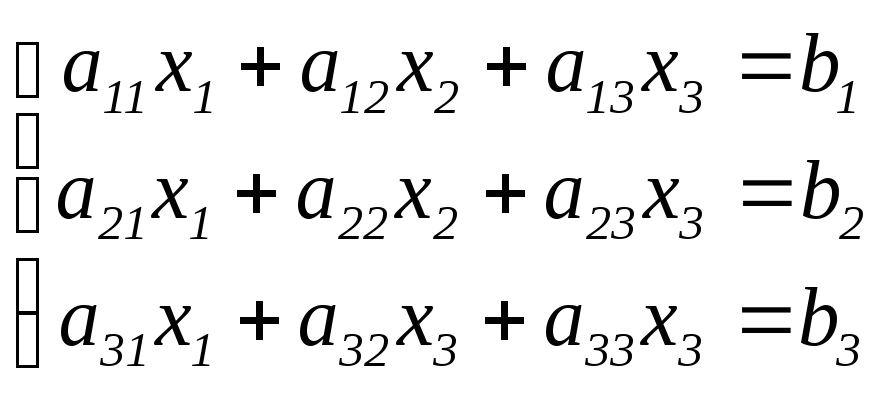(2)

Метод Гаусса решения системы (2) состоит в следующем:

Разделим все члены первого уравнения на , а затем, умножив полученное уравнение на , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное будет исключено, и получится система вида:

(3)

Теперь разделим второе уравнение системы (3) на, умножим полученное уравнение на и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное будет исключено и получиться система треугольного вида:

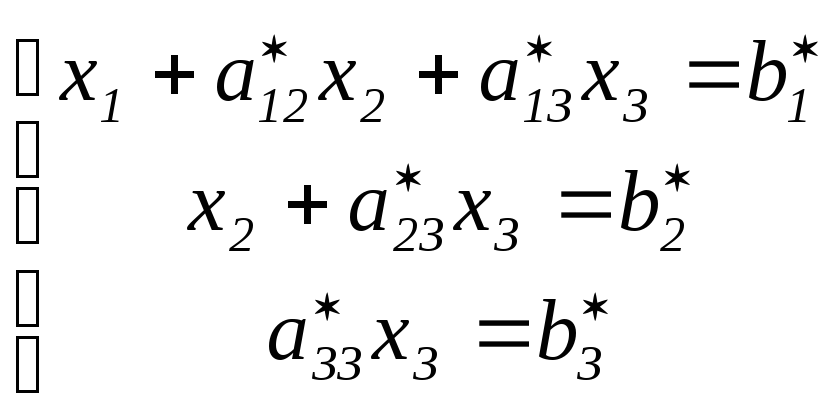(4)

Из последнего уравнения системы (4) находим , подставляя найденное подставляя найденное значение в первое уравнение, находим .

Пример. Решим систему уравнений методом Гаусса:

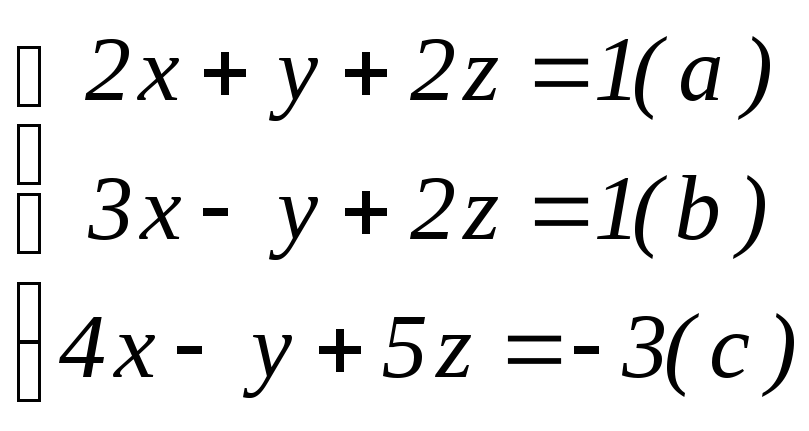
Решение.

Разделив уравнение (а) на 2, получим систему

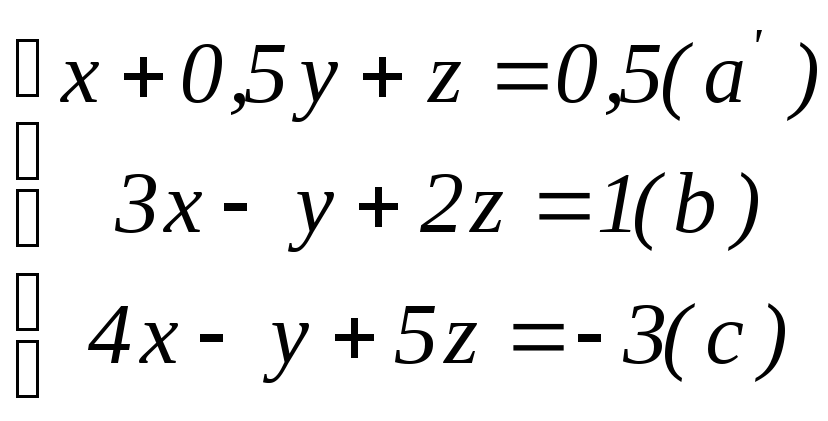
Вычтем из уравнения (b) уравнение , умноженное на 3, а из уравнения (c) - уравнение , умноженное на 4.

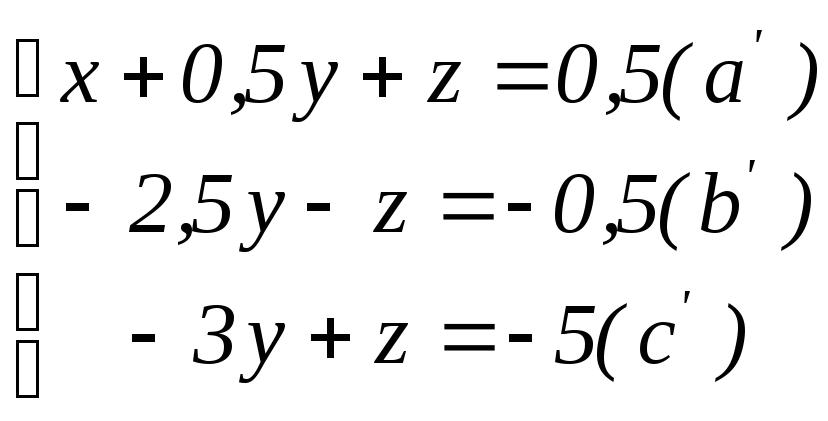
Разделив уравнение () на – 2,5 , получим:

Вычтем из уравнения () уравнение , умноженное на – 3:

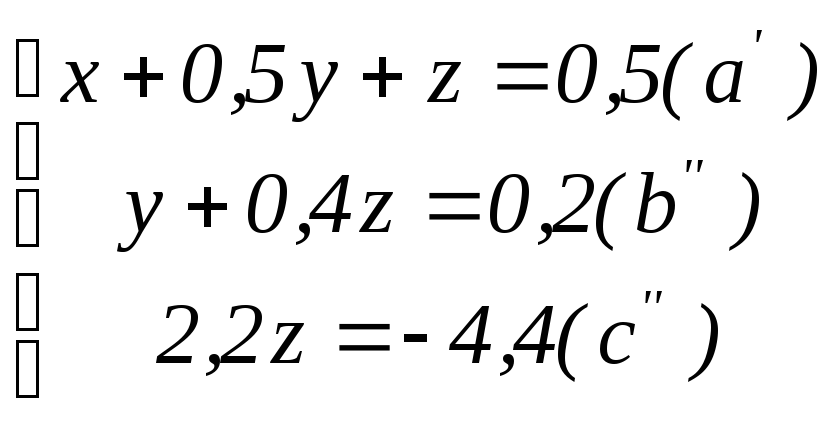
Из уравнения находим Z = -2; подставив это значение в уравнение , получим Y=0,2-0,4Z=0,2-0,4(-2)=1; наконец , подставив значение Z=-2 и Y=1 в уравнение(a¹) , находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2)=2. Итак, получаем ответ X=2, Y=1, Z=-2 .

Проверка.

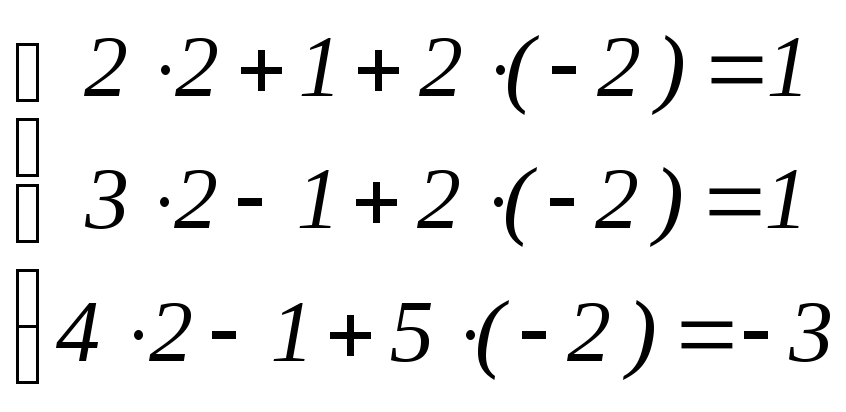
14. Комплексные числа. Основные понятия. Геометрическое изображение. Формы записи комплексных чисел.

Комплексным числом z называется выражение вида z = x + iy, где x и y – действительные числа, а i – мнимая единица, т.е. i² = -1.

Если x = 0, то число 0 + iy называется чисто мнимым.

Если y = 0, то число x + i0 отождествляется с действительным числом x, а это означает, что множество всех действительных чисел R является подмножеством всех комплексных чисел C.

z = x + iy = 0, когда x = y = 0. Понятие больше и меньше для комплексных чисел не вводится.

Число x называется действительной частью комплексного числа z и обозначается x = Re z, а y называется мнимой частью числа z и обозначается y = Im z.

Два комплексных числа и называются равными тогда и только тогда, когда равны их действительные и мнимые части: и .

Два комплексных числа и называются сопряженными.

Под модулем комплексного числа z понимается неотрицательное число .

Геометрическое изображение комплексных чисел.

Всякое комплексное число можно изобразить на плоскости Oxy следующим образом: x = Re z, y = Im z.

y

y M

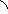
O x x

На оси Ox расположены действительные числа, поэтому она называется действительной осью. На оси Oy расположены чисто мнимые числа, поэтому она называется мнимой осью.

Удобной является интерпретация комплексного числа как радиуса-вектора .

Длина вектора называется модулем комплексного числа .

Угол между действительной осью и вектором называется аргументом комплексного числа Arg z =. Аргумент считается положительным или отрицательным в зависимости от того, ведется ли его отсчет от положительного направления действительной оси против или по часовой стрелке соответственно.

По заданной точке z ее модуль определяется единственным образом, а аргумент – с точностью до слагаемого , k = 0, 1, 2 и т.д. Значение аргумента , удовлетворяющее условию называется главным и обозначается arg z.

В точке z = 0 аргумент не определен.

Таким образом, Arg z = arg z + .

Формы записи комплексных чисел.

1. Запись комплексного числа z в виде (1) называется алгебраической формой комплексного числа.

2. Положение комплексного числа на плоскости удобно представлять в полярных координатах.

Модуль r и аргумент комплексного числа можно рассматривать как полярные координаты вектора , изображающего комплексное число .

Тогда , ,

(2)

Такая запись называется триганометричекой записью комплексного числа.

, , , .

Так как = Arg z = arg z + , то , поэтому при переходе от алгебраической формы комплексного числа к триганометрической достаточно определить .

3. Используя формулу Эйлера комплексное число можно записать в так называемой показательной (экспоненциальной) форме

, (3)

где - модуль комплексного числа, а = Arg z = arg z + - аргумент.

В силу формулы Эйлера функция - периодическая с основным периодом .