19. Гипербола и парабола. Уравнение плоскости и прямой в пространстве.

Гиперболой называется множество всех точек плоскости, разность расстояний каждой из которых до двух данных точек и (называемых фокусами гиперболы) есть величина постоянная, равная 2a.

П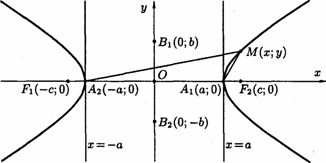усть М(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы или , т.е.

.

После упрощений получим каноническое уравнение гиперболы.

Каноническое уравнение гиперболы имеет вид , где .

Подобно эллипсу гипербола симметрична относительно обеих осей координат. Она состоит из двух частей, которые называются ее ветвями. Гипербола пересекает ось Ox в двух точках, называемых вершинами гиперболы, отрезок между вершинами называется вещественной осью гиперболы.

Прямые называются асимптотами гиперболы.

Эксцентриситетом гиперболы называется отношение .

При построении гиперболы целесообразно сначала построить основной прямоугольник гиперболы со сторонами 2a и 2b, параллельными координатным осям, и с центром в начале координат, провести прямые, проходящие через противоположные вершины этого прямоугольника, – асимптоты гиперболы и отметить вершины и гиперболы.

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки F, называемой фокусом, и данной прямой l, называемой директрисой.

Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0).

В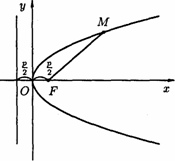 выбранной системе фокус F имеет координаты , а уравнение директрисы имеет вид .

Уравнение называется каноническим уравнением параболы.

Вершиной параболы называется точка пересечения параболы с ее осью симметрии.

К параболам относятся также кривые, заданные уравнениями:

, .

Уравнение плоскости в пространстве.

Уравнение = 0 определяет в пространстве некоторую поверхность.

Пусть дана точка М₀ = (x₀, y₀, z₀) и ненулевой вектор (A,B,C). Построим в декартовой системе координат плоскость, проходящую через точку М₀, перпендикулярно к вектору (этот вектор называют нормальным вектором или нормалью плоскости).

Рассмотри произвольную точку этой плоскости. Так как вектор лежит на плоскости, то он перпендикулярен к вектору .

Следовательно, их скалярное произведение равно нулю: .

Преобразуем в координатную форму:

(1)

Введя обозначение , уравнение (1) можно переписать в виде:

(2)

Уравнение (2) называется общим уравнением плоскости.

Определение. Общее уравнение называется полным, если все его коэффициенты отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, то уравнение называется неполным.

Уравнение , где , , называется уравнением плоскости в «отрезках».

Виды неполных уравнений:

1) D = 0. Плоскость проходит через начало координат.

2) A = 0. Плоскость параллельно оси Ox (аналогично для других коэффициентов).

3) A = 0, B = 0. Плоскость параллельна координатной плоскости xOy.

4) A = 0, B = 0, С = 0. Плоскость представляет собой координатную плоскость.

Уравнение прямой в пространстве.

Рассмотрим систему уравнений:

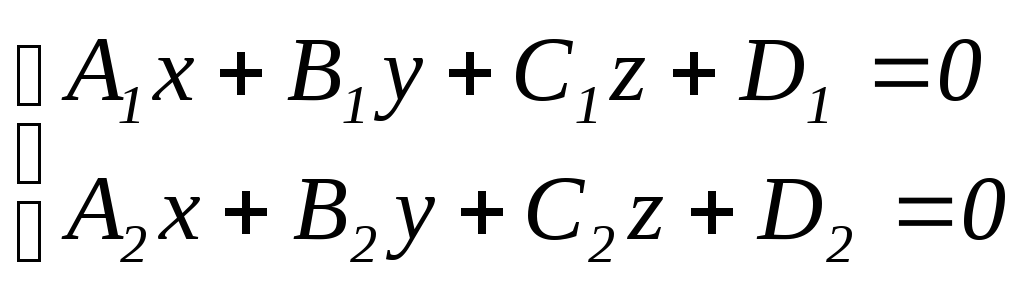(1)

Каждое из уравнений системы определяет плоскость. Если плоскости не параллельны, то система (1) определяет прямую как линию пересечения этих плоскостей. Уравнения (1) называются общим уравнением прямой.

Уравнение прямой в пространстве, проходящей через две данные точки

Каноническое уравнение прямой

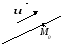
где (х₀; у₀; z₀) – точка прямой,

(k; l; m) – направляющий вектор.