29.Деякі важливі границі:

1. Нехай ,тоді , якщо , то , маємо

2. Нехай ,тоді , якщо , то , маємо

3.

Елементарні ф-ції

Ел-ми ф-ми називають фун-ції які утв-ся з осн-х елементарних ф-цій за допомогою скінченого числа арифм. Ф-цій і суперпозицій. Оск. основні елементарні функції неперервні у всіх точках в яких вони визначені, то теореми про операції над неперервними ф-ціями і неперервності складної ф-ції слідує теорема(Всяка елементарна ф-ція неперервна в кожній точці в якій вона визначена)

4.

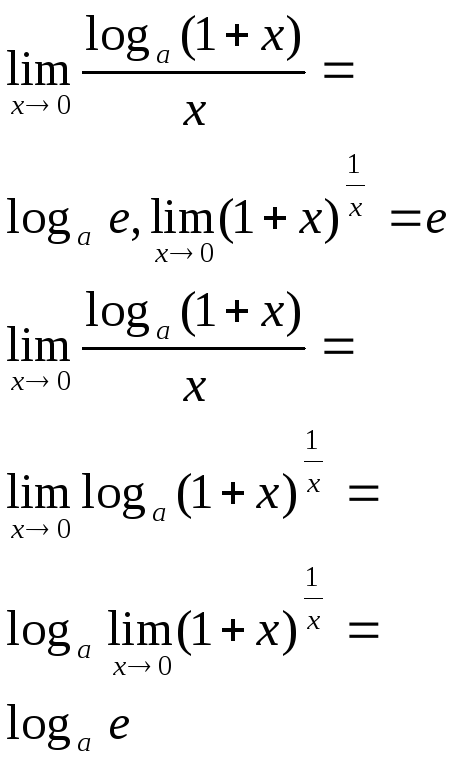
При доведенні даної рівності ми застосували правило граничного переходу для неперервної ф-ції.

5.

6.

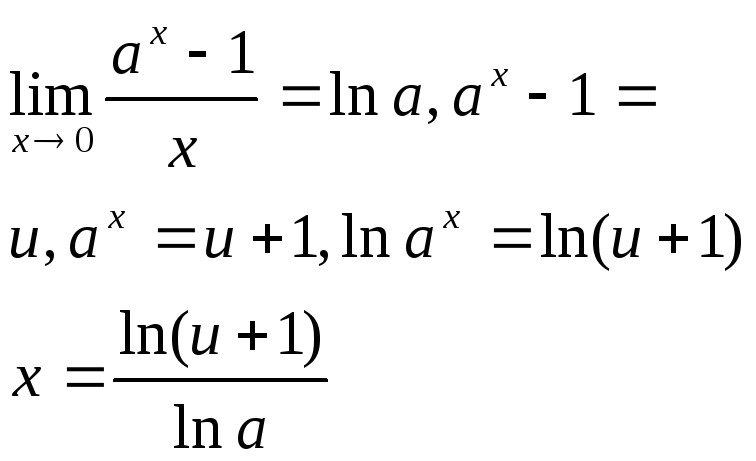
Оск. Показникові ф-ція неперервна, то якщо . Маємо

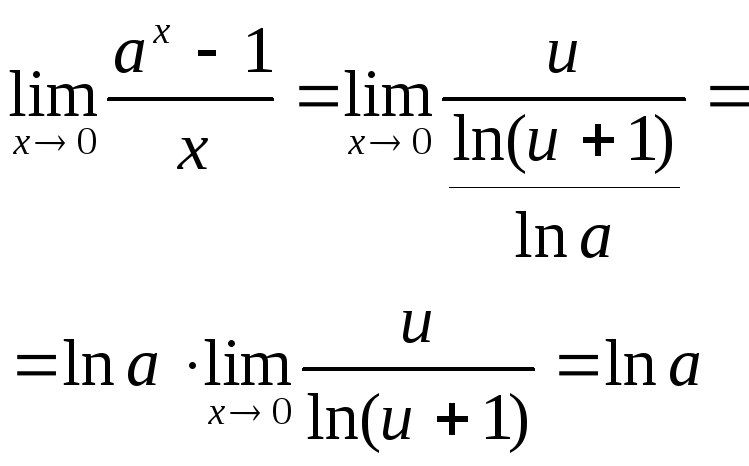
7.

8.

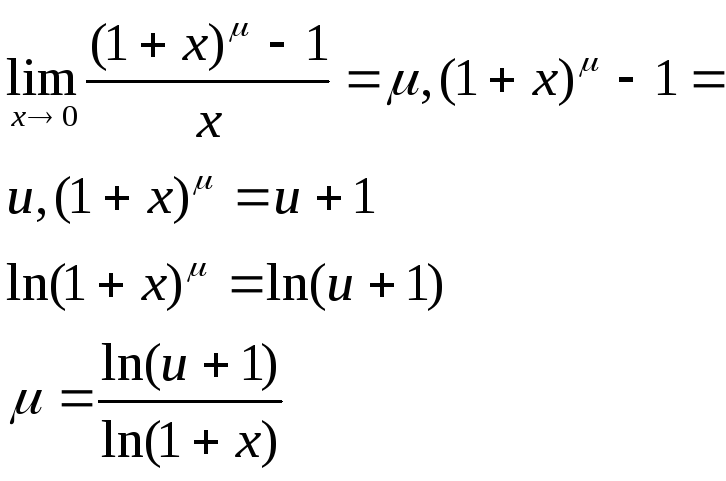
Оск. лог ф-ція неперервна то при маємо 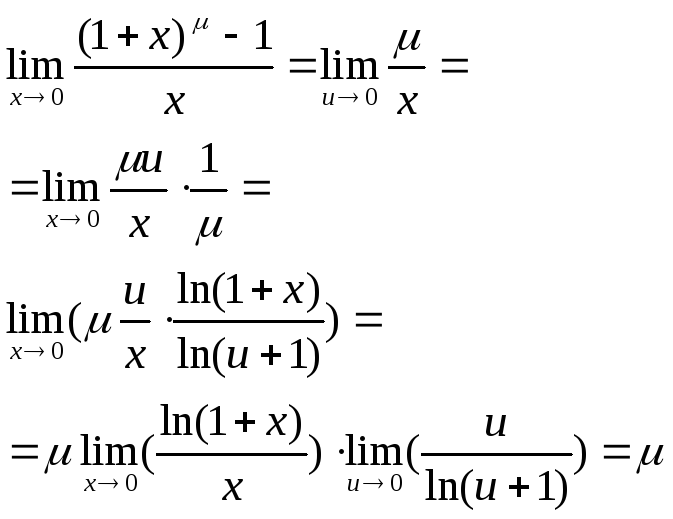30.Похідна ф-ції в точці. Механічний і фізичний зміст похідної.

Розглянемо задачу про швидкість матер-ї точки.

Нехай точка рух-ся нерівномірно вздовж даної прямої і нехай шлях цієї точки є ф-цією від t.

Нехай з моменту часу t пройшов деякий час , за який точка з положення в положення , пройшовши шлях .

За час точка пройшла шлях

. Середньою швидкістю матеріальної точки за проміжок часу

, при чому чим менший є проміжок відносно моменту часу t тим точніше середня швидкість відповідає швидкості руху точки у даний момент часу.

Істинну (миттєву) швидкість руху точки знаходять як границю , якщо , тобто Нехай ця ф-ція визначена на деякому проміжку.

Візьмемо т. з цього проміжку і надамо її приріст , але так щоб належала ОВ, тоді ф-ція буде мати приріст

Озн. Похідною ф-ції в т. називається границя відношення приросту ф-ції в цій точці до приросту аргументу , коли приріст аргументу прямує до 0.

З означення похідної випливає, що швидкість у даний момент часу є похідна від пройденого шляху по .

у цьому полягає механічний зміст похідної.

Узагальнюючи можна сказати, що коли ф-ція описує деякі процеси, то похідна відображає швидкість зміни цього процесу, у цьому полягає фіз. зміст похідної.

31.Геометричний зміст похідної, рівняння дотичної.

Розглянемо просту неперервну криву, зафіксуємо на ній точку , нехай - довільна точка кривої. Через точки і проведемо пряму (січну).

Озн. Дотичної до даної кривої у точці наз-ся граничне положення січної при умові що точка необмежено наближається до точки , вздовж кривої

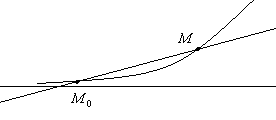
Розглянемо деякі криві, що задані у прямокутних координатах рівнянням і в т. знайдемо кут нахилу дотичної до додатного напряму осі .Будемо вважати, що в т. крива має дотичну не перпендикулярну до осі .

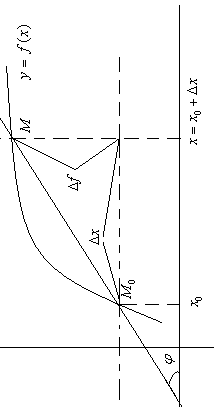
Через вказану і довільну проведемо . Позначимо - кут що утв. З додатним напрямком осі січна .

Через -кут нахилу дотичної до ,до додатного напряму осі у т. . Зрозуміло що Очевидно, що коли прямує до 0 ,, . Тому

Т.ч. , що утворює дотична в т. з дод. Напрямом осі дорівнює значенню похідної - у цьому полягає геометричний змісь похідної.

З геометрії відомо що рівняння прямої що проходить через т. і кут коеф. К має вигляд , звідси одержимо рівняння дотичної в т.

Озн. Нормаль до кривої в т. - пряма яка проходить через т. перпендикулярно дотичній в цій точці.

З геометрії відомо, що кутові коефіцієнти і двох перпендикулярних прямих відносяться як рівняння нормалі в т.

32.Неперервність і диференційованість

Односторонні похідні визначаються за допомогою односторонніх границь. Нехай ф-ція визначена у деякому околі т. .

Якщо у формулі припустимо що , то відповідну границю називають правою похідною ф-ції в т. . Якщо припустимо що , то відповідну границю наз-ть лівою похідн6ою в т.

Праву похідну позначають символом

Ліву похідну позначають символомЯкщо визначена на відрізку , то похідною в т. розуміють праву похідну, а в т. - ліву похідну.Коли ф-ція має праву і ліву похідну в т. і ці похідні рівні, то в т. існує похідна , якщо , то похідна в т. не існує. Не існує похідної також в т-ках розриву ф-ції.

Якщо в т. границя , то похідну в цій точці наз-ть нескінченною.

Озн. Ф-ція називається диференційованою в т. якщо вона має похідну .

Ф-ція називається диференційованою на проміжку якщо вона диференційована у кожній точці проміжку.

Приклади.

Теорема: Якщо ф-ція диференційована в т. , то вона неперервна у цій точці.

Доведення: За умовою теореми . За теоремою про необхідну і достаню умову існування границі ф-ції в точці , де якщо , тоді якщо , то . Тобто нескінченно малому приросту аргументу відповідає нескінченно малий приріст ф-ції. Тоді за означенням неперервності

ф-ція - неперервна у точці . Теорема доведена.

Зауваження: наведений приклад ф-ції вказує, що твердження обернене до даної теореми взагалі кажучи не виконується: з неперервності ф-ції на проміжку не випливає диференційованість цієї ф-ції у кожній точці данного проміжку.