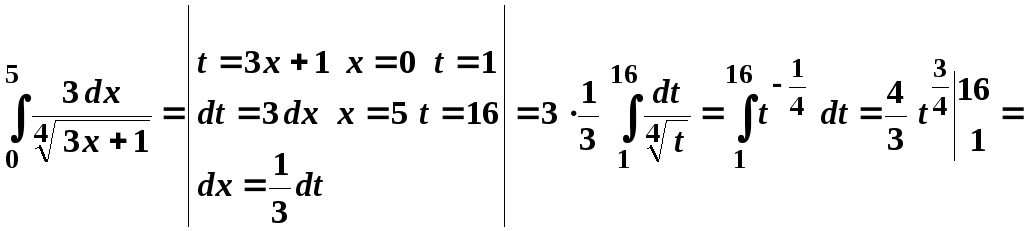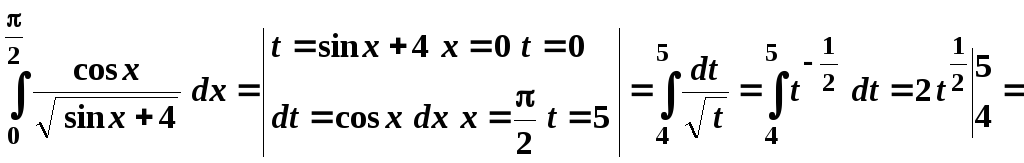- •Содержание
- •Введение
- •Программа курса высшей математики
- •Тема 1. Аналитическая геометрия на плоскости
- •Тема 2. Введение в математический анализ. Предел и непрерывность функций
- •Тема 3. Производная и дифференциал. Исследование функций
- •Тема 4. Неопределенный интеграл
- •Тема 5. Определенный интеграл
- •Тема 6. Приложения определенного интеграла
- •Вопросы для самопроверки
- •Тема 7. Определенный интеграл. Несобственный интеграл
- •Рассмотрим решение примеров.
- •Вопросы для самопроверки
- •Тема 8. Геометрические и экономические приложения определенного интеграла
- •Экономический смысл интеграла
- •Литература
- •Указания к выполнению контрольной работы 1
- •Тема 1. Элементы аналитической геометрии на плоскости
- •Вопросы для самопроверки
- •Тема 2. Введение в математический анализ (предел функции, непрерывность)
- •Вопросы для самопроверки
- •Тема 3. Производная
- •Краткие теоретические сведения.
- •Основные формулы дифференцирования
- •Вопросы для самопроверки
- •Тема 4. Применение производной к исследованию функций
- •Краткие теоретические сведения. Общий план исследования функций
- •Для исследуемой функции
- •Вопросы для самопроверки
- •Тема 5. Предельный анализ в экономике
- •Предельный анализ в экономике
- •Предельный доход
- •Тема 6. Первообразная и неопределенный интеграл
- •Правила интегрирования
- •1. Метод непосредственного интегрирования
- •2. Метод замены переменной ( метод подстановки )
- •3. Интегрирование по частям
- •Задания к контрольной работе 1
- •Задания к контрольной работе 2
Рассмотрим решение примеров.
 .
.
![]()
При вычислении определенных интегралов методом интегрирования по частям переменная интеграции не изменяется, поэтому не изменяются и пределы интегрирования.
Формула интегрирования по частям для определенного интеграла имеет вид:
![]()
Применим формулу для вычисления определенных интегралов
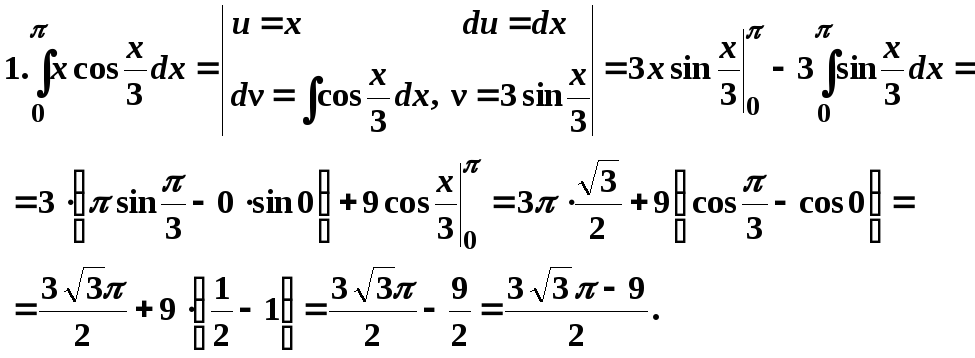
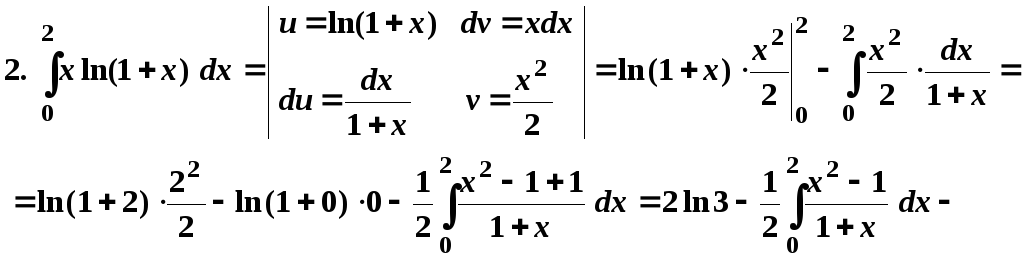
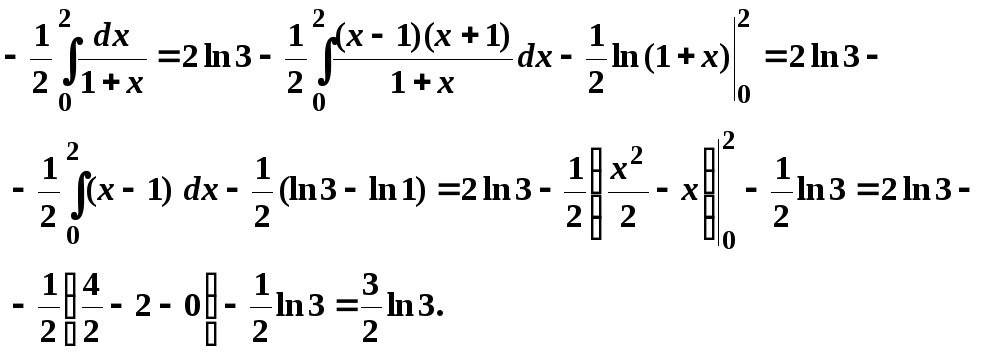
Понятие
несобственного
интеграла
является обобщением понятия определенного
интеграла. В теории вероятностей важную
роль играет интеграл Пуассона
![]() ,
который является несобственным интегралом
с полубесконечным интервалом интегрирования
от функции
,
который является несобственным интегралом
с полубесконечным интервалом интегрирования
от функции
![]()
Если
существует конечный предел
![]() ,
то этот предел называется несобственным
интегралом от функции
,
то этот предел называется несобственным
интегралом от функции
![]() на
интервале
на
интервале
![]() и
обозначается
и
обозначается
![]() .
В этом случае говорят, что интеграл
сходится. Если же конечного предела не
существует, то несобственный интеграл
расходится.
.
В этом случае говорят, что интеграл
сходится. Если же конечного предела не
существует, то несобственный интеграл
расходится.
Рассмотрим решения примеров:
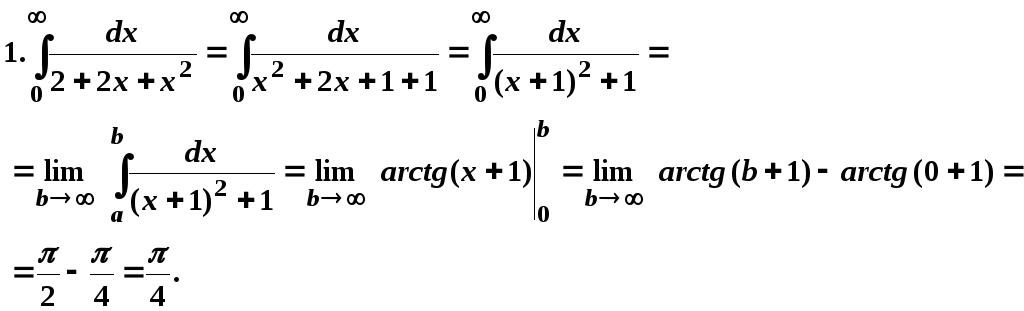 Таким
образом, несобственный интеграл сходится
и равен
Таким
образом, несобственный интеграл сходится
и равен
![]()
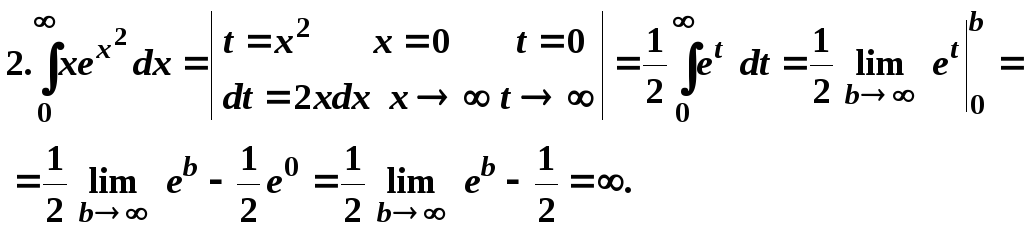
Предела не существует, следовательно, несобственный интеграл конечного расходится.
Вопросы для самопроверки
-
Что называется интегральной суммой от функции
 на
интервале
на
интервале
а ; b?
-
Дайте определение определенного интеграла как предела интегральных сумм.
-
Каков геометрический смысл определенного интеграла?
-
Сформулируйте свойства определенного интеграла.
-
Запишите формулу Ньютона–Лейбница.
-
Запишите формулу интегрирования методом замены переменной в определенном интеграле.
-
Запишите формулу интегрирования по частям в определенном интеграле.
-
Что называется несобственным интегралом?
-
В каком случае несобственный интеграл сходится? Расходится?
Тема 8. Геометрические и экономические приложения определенного интеграла
Литература:
-
Высшая математика для экономистов. Учебник / Под ред. проф.
Н.Ш. Кремера. М., 1997. Гл. 11. § 9, 10.
-
Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. М., 1982. Гл. 12. § 6.
Понятие
определенного интеграла вводится таким
образом, что в случае, когда функция
![]() неотрицательна на отрезке а
, b,
определенный интеграл
неотрицательна на отрезке а
, b,
определенный интеграл
![]() численно равен площади, ограниченной
кривой
численно равен площади, ограниченной
кривой
![]() ,
осью ОХ
и прямыми
,
осью ОХ
и прямыми
![]() :
:
![]()
В
случае, когда функция
![]() отрицательна на отрезке а
, b
,
отрицательна на отрезке а
, b
,
![]()
Если
плоская фигура ограничена двумя линиями
![]() и
и
![]() ,
то
,
то
![]()
Рассмотрим решение примеров.
1)
Вычислить площадь фигуры, заключенной
между кривой
![]() и осью OX.
и осью OX.
Найдем координаты вершины параболы:
![]() и
точки пересечения с осью OX:
и
точки пересечения с осью OX:
![]()
Построим параболу. Площадь, заштрихованную на чертеже, необходимо вычислить.

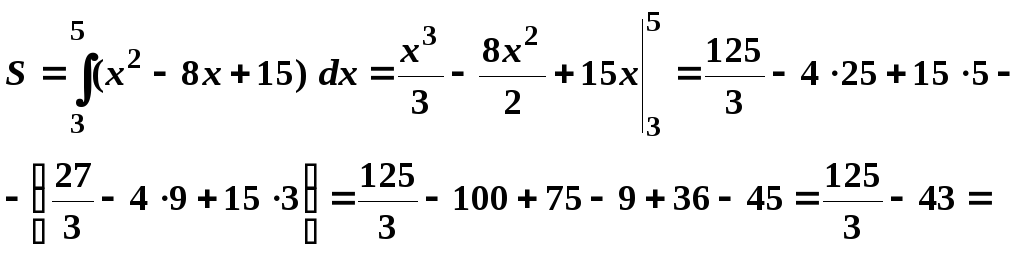
![]() кв. ед.
кв. ед.
2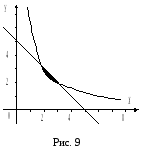 )
Вычислить площадь фигуры, заключенной
между кривой
)
Вычислить площадь фигуры, заключенной
между кривой
![]() и прямой
и прямой
![]() .
.
Построим
гиперболу
![]() и прямую
и прямую
![]() .
.
Найдем
точки пересечения кривой
![]() и прямой
и прямой
![]()
![]()
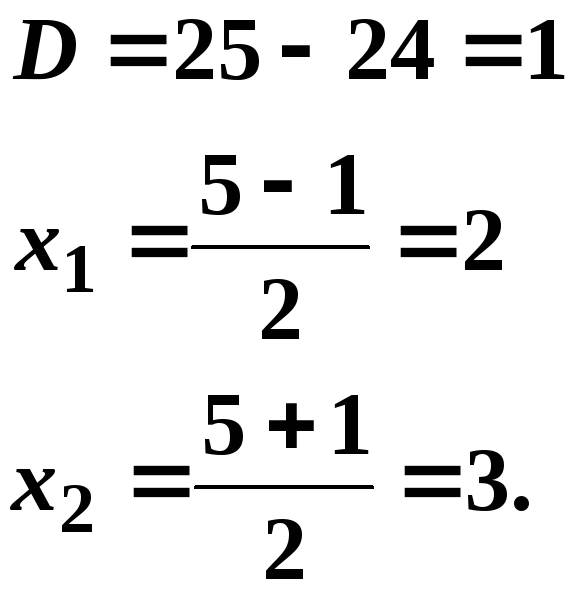
Тогда площадь плоской фигуры будет равна
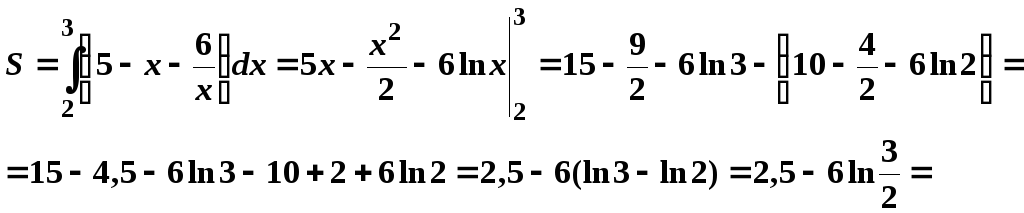
![]() кв.ед.
кв.ед.
Экономический смысл интеграла
Более подробно остановимся на применении неопределенного и определенного интегралов в экономических задачах.
Если
рассматривать издержки производства
как функцию количества выпускаемой
продукции
![]() ,
то отношение приращения издержек
производства С
к приросту продукции Q
даст среднее издержки производства на
единицу продукции
,
то отношение приращения издержек
производства С
к приросту продукции Q
даст среднее издержки производства на
единицу продукции
![]() Производная
Производная
![]() выражает
предельные издержки производства и
характеризует приближенно дополнительные
затраты на производство единицы
дополнительной продукции.
выражает
предельные издержки производства и
характеризует приближенно дополнительные
затраты на производство единицы
дополнительной продукции.
Предельные издержки зависят от уровня производства и определяются не постоянными производственными затратами (производственные помещения, оборудование и т.п.), а лишь переменными затратами на сырье, топливо, рабочую силу.
Интегрирование позволяет решить обратную задачу: по заданной функции предельных издержек производства найти суммарные затраты.
Пусть для некоторой фирмы предельные издержки имеют вид:
![]()
Требуется найти суммарные затраты при условии, что постоянные издержки равны 90 условных единиц.
Очевидно,
что
![]()
При условии, что постоянные издержки, не зависящие от объема производства, равны 90 ед., найдем постоянную интегрирования С:
![]() ,
отсюда С
= 90.
,
отсюда С
= 90.
Тогда суммарные затраты на производство будут равны:
![]()
Если рассмотреть простую двухсекторную макроэкономическую модель национального дохода Y, то он представляется суммой потребления С и сбережений S, идущих на капиталовложения или инвестиции:
![]()
Очевидно,
что потребление и сбережение являются
функциями национального дохода:
![]() и вопрос состоит в том, как они будут
изменяться с изменением национального
дохода. Для решения этого вопроса
вводятся понятия
предельной склонности к потреблению и
предельной склонности к сбережению,
которые определяются как производные:
и вопрос состоит в том, как они будут
изменяться с изменением национального
дохода. Для решения этого вопроса
вводятся понятия
предельной склонности к потреблению и
предельной склонности к сбережению,
которые определяются как производные:
![]()
Решим
обратную задачу. Требуется определить
потребление С,
если известна предельная склонность к
потреблению, заданная зависимостью
![]() и
потребление составляет 85
единиц, когда национальный доход равен
100
единицам.
и
потребление составляет 85
единиц, когда национальный доход равен
100
единицам.
![]()
Найдем постоянную интегрирования С, подставляя С = 85 при Y =100.
![]() тогда
С
= 33.
тогда
С
= 33.
Следовательно, для функции потребления получаем:
![]()
Можно
дать прогноз, что при национальном
доходе в 200
единиц потребление составит
![]() .
Тогда инвестиции возрастут с 100
– 85
= 15
единиц до 200
– 135,8 =
64,2
единиц. В этом случае национальный доход
вырос в два раза, а инвестиции возросли
больше, чем в четыре раза.
.
Тогда инвестиции возрастут с 100
– 85
= 15
единиц до 200
– 135,8 =
64,2
единиц. В этом случае национальный доход
вырос в два раза, а инвестиции возросли
больше, чем в четыре раза.
Дадим
понятие определенного интеграла. Пусть
на отрезке а,b
задана функция
![]() Разобьем отрезок а,
b
на элементарные отрезки шириной хi
и значение функции в некоторой точке
каждого отрезка
Разобьем отрезок а,
b
на элементарные отрезки шириной хi
и значение функции в некоторой точке
каждого отрезка
![]() Сумму
вида
Сумму
вида
![]() назовем интегральной суммой функции
назовем интегральной суммой функции
![]() на отрезке а,
b,
она будет зависеть от способа разбиения
отрезка на элементарные отрезки и выбора
точек
на отрезке а,
b,
она будет зависеть от способа разбиения
отрезка на элементарные отрезки и выбора
точек
![]() .
Если предел последовательности
интегральных сумм при max
хi0
не зависит
от способа разбиения и выбора точек
.
Если предел последовательности
интегральных сумм при max
хi0
не зависит
от способа разбиения и выбора точек
![]() и существует, то он называется определенным
интегралом функции
и существует, то он называется определенным
интегралом функции
![]() на отрезке а,b
и обозначается
на отрезке а,b
и обозначается
![]() .
.
На основании изложенного рассмотрим экономический смысл определенного интеграла.
Пусть
функция
![]() есть производительность труда, которая
зависит от времени. Найдем объем продукции
и,
произведенный за промежуток времени
0,
Т.
Отрезок 0,
Т
разобьем точками ti
на частичные отрезки ti;
за промежуток времени ti
объем произведенной продукции
есть производительность труда, которая
зависит от времени. Найдем объем продукции
и,
произведенный за промежуток времени
0,
Т.
Отрезок 0,
Т
разобьем точками ti
на частичные отрезки ti;
за промежуток времени ti
объем произведенной продукции
![]() ,
где
,
где
![]() Весь объем продукции
Весь объем продукции
![]() ,
,
что, согласно предыдущему, есть определенный интеграл и тогда
![]()
![]()
Связь между определенным и неопределенным интегралами устанавливает формула Ньютона-Лейбница:
![]()
Используя
экономический смысл определенного
интеграла и формулу Ньютона-Лейбница,
найдем объем продукции, произведенной
за четыре года, если производительность
труда зависит от времени как
![]() .
.
Тогда