
- •Раздел 2. Дифференциальное исчисление 138
- •Раздел 2. Дифференциальное исчисление лекция 2.1. Множества. Операции над множествами. Отображение множеств. Мощность множества. Множество действительных чисел
- •2.1.1. Множества. Операции над множествами. Отображение множеств
- •Свойства.
- •2.1.2. Множество действительных чисел
- •Лекция 2.2. Переменная величина. Функция одной и нескольких переменных. Способы задания. Основные элементарные функции, их свойства и графики
- •2.2.1. Переменная величина
- •2.2.2. Функция одной и нескольких переменных
- •2.2.3. Способы задания функции
- •2.2.4. Основные свойства функции
- •2.2.5. Классификация функций. Основные элементарные функции, их свойства и графики
- •Основные элементарные функции
- •Лекция 2.3. Предел переменной величины. Предел последовательности. Предел функции в точке. Бесконечно малые и бесконечно большие функции
- •2.3.1. Предел переменной величины.
- •2.3.2. Предел функции
- •2.3.3.Бесконечно малая и бесконечно большая функции, их свойства
- •Лекция 2.4. Теоремы о пределах и их применение. Признаки существования пределов
- •2.4.1. Теоремы о пределах
- •2.4.2. Признаки существования пределов
- •Лекция 2.5. Первый замечательный предел. Второй замечательный предел. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •2.5.1. Первый замечательный предел
- •2.5.2. Второй замечательный предел
- •2.5.3. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •Лекция 2.6. Приращение функции одной и двух переменных. Непрерывность функции одной и двух переменных. Точки разрыва
- •2.6.1. Приращение функции одной и двух переменных
- •2.6.2. Непрерывность функции одной и двух переменных
- •2.6.3. Точки разрыва
Лекция 2.4. Теоремы о пределах и их применение. Признаки существования пределов
2.4.1. Теоремы о пределах
Правила, по которым
находятся пределы функций, включают
теоремы, справедливые для функции любого
числа переменных при
![]() и при
и при
![]() .
.
Эти теоремы позволяют находить пределы в тех случаях, когда функции представляют собой результат арифметических действий над другими функциями, пределы которых существуют и заранее известны.
Теорема 1.
Предел постоянной равен самой постоянной,
т.е. если
![]() ,
то
,
то
![]() .
.
Теорема 2.
Предел суммы конечного числа функций
в точке
![]() равен сумме пределов этих функций в
этой точке:
равен сумме пределов этих функций в
этой точке:
![]()
![]() .
.
Доказательство:
Приведем
доказательство для суммы двух функций.
Докажем, что
![]() .
.
Пусть
![]() и
и
![]() .
Тогда по теореме 7 (п.2.3.3) можно записать
.
Тогда по теореме 7 (п.2.3.3) можно записать
![]() и
и
![]() .
.
Следовательно,
![]() ,
где
,
где
![]() бесконечно малая функция как сумма
бесконечно малых функций. Тогда по
теореме 7 (п.2.3.3) можно записать
бесконечно малая функция как сумма
бесконечно малых функций. Тогда по
теореме 7 (п.2.3.3) можно записать
![]() ,
т.е.
,
т.е.
![]() .
Ч.
и т.
д.
.
Ч.
и т.
д.
В случае разности двух функций и суммы любого конечного числа функций доказательство аналогично.
Следствие 1.
Функция
может иметь только один предел при
![]() .
.
Теорема 3.
Предел произведения конечного числа
функций в точке
![]() равен произведению пределов этих функций
в этой точке:
равен произведению пределов этих функций
в этой точке:
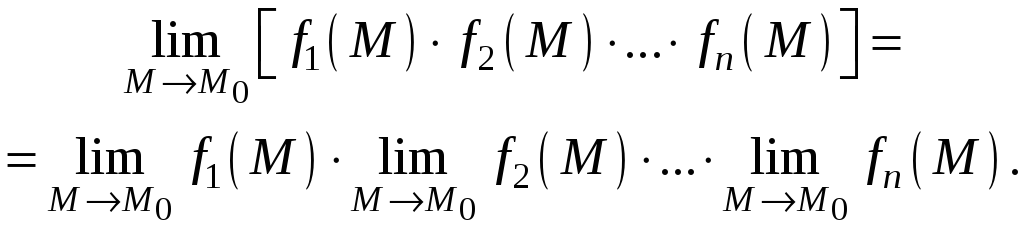
Следствие 2. Постоянный множитель можно выносить за знак предела:
![]() .
.
Теорема 4. Предел дроби равен пределу числителя, делимому на предел знаменателя, если предел знаменателя не равен нулю:
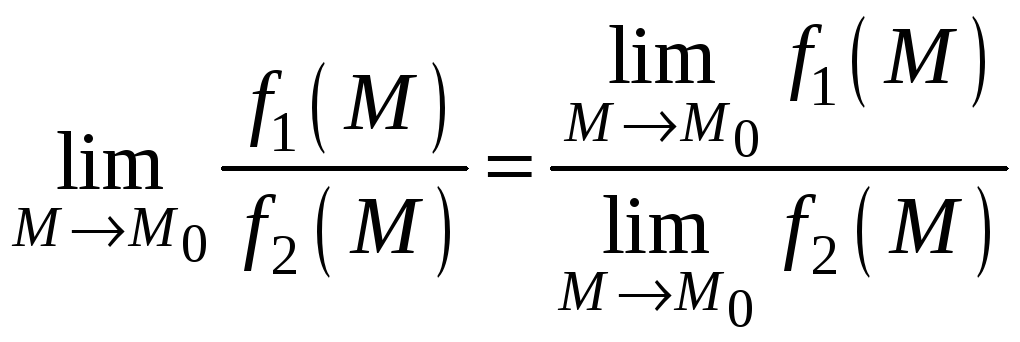
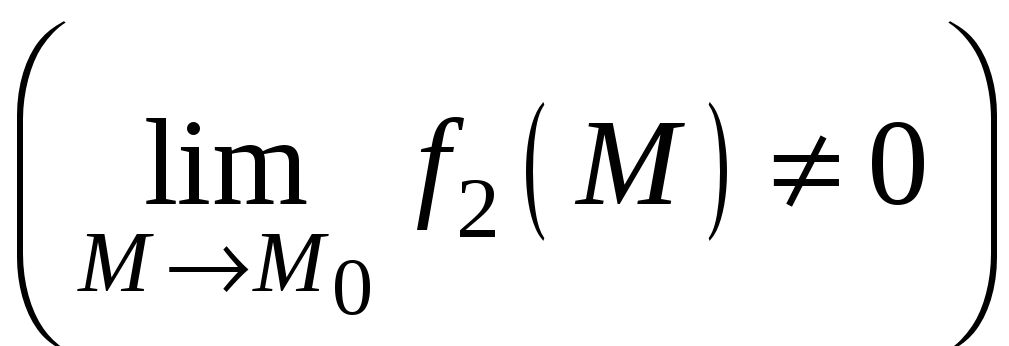 .
.
Примеры.
1. Найти
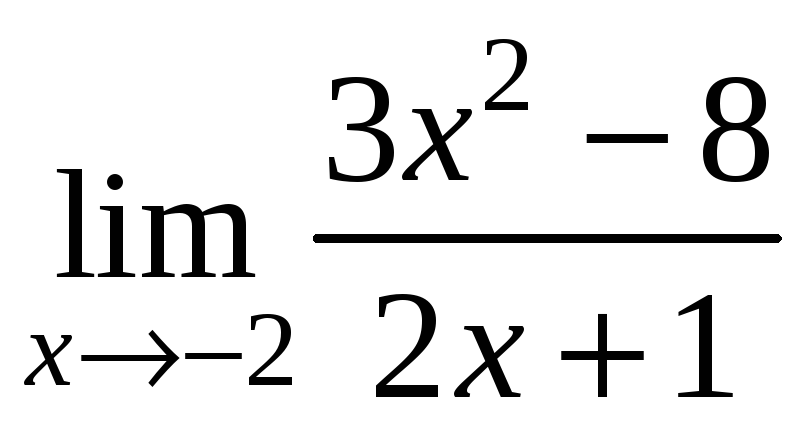 .
.
Решение:
В данном случае предел функции, стоящей
в знаменателе, при
![]() отличен от нуля, поэтому можно применить
приведенные выше теоремы:
отличен от нуля, поэтому можно применить
приведенные выше теоремы:
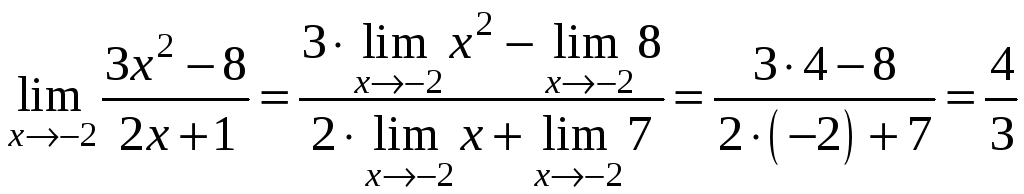 .
.
Иначе говоря, в данном случае, чтобы найти предел, можно вместо независимой переменной подставить её значение в предельной точке.
2.
Найти
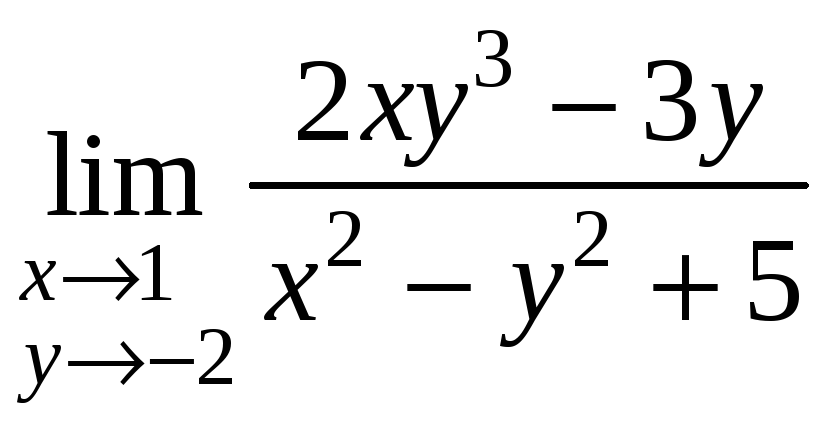 .
.
Решение:
Функция
![]() ,
стоящая в знаменателе дроби при
,
стоящая в знаменателе дроби при
![]() и
и
![]() стремится к числу
стремится к числу
![]() ,
тогда
,
тогда
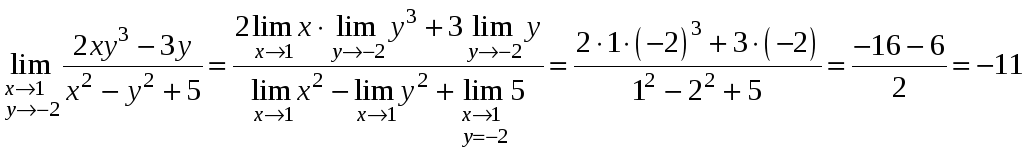 Пример
аналогичен предыдущему: вместо независимых
переменных необходимо подставить их
значения в предельной точке.
Пример
аналогичен предыдущему: вместо независимых
переменных необходимо подставить их
значения в предельной точке.
3.
Найти
![]() .
.
Решение:
Предел знаменателя
![]() при
при
![]() равен нулю и теорема 4 не применима. В
данном случае воспользуемся свойством
бесконечно малой функции (см. п.2.3.3
теорема 6). Функция
равен нулю и теорема 4 не применима. В
данном случае воспользуемся свойством
бесконечно малой функции (см. п.2.3.3
теорема 6). Функция
![]() – бесконечно малая при
– бесконечно малая при
![]() ,
тогда обратная ей дробь
,
тогда обратная ей дробь
![]() – бесконечно большая функция, а значит
– бесконечно большая функция, а значит
![]() .
.
Таким образом,
если знаменатель дроби не обращается
в ноль, то чтобы найти такой предел,
достаточно в выражение функции подставить
предельные значения независимых
аргументов. Если же знаменатель стремиться
к нулю
![]() ,
а числитель к некоторому постоянному
числу, то при нахождении предела
используют свойство бесконечно малой
величины (см. п.2.3.3 теорема 6).
,
а числитель к некоторому постоянному
числу, то при нахождении предела
используют свойство бесконечно малой
величины (см. п.2.3.3 теорема 6).
В случае неопределенных
выражений, характеризуемых условно
символами:
 (будем называть их неопределенностями),
которые возникают при отыскании предела
выражений:
(будем называть их неопределенностями),
которые возникают при отыскании предела
выражений:
![]() ;
;
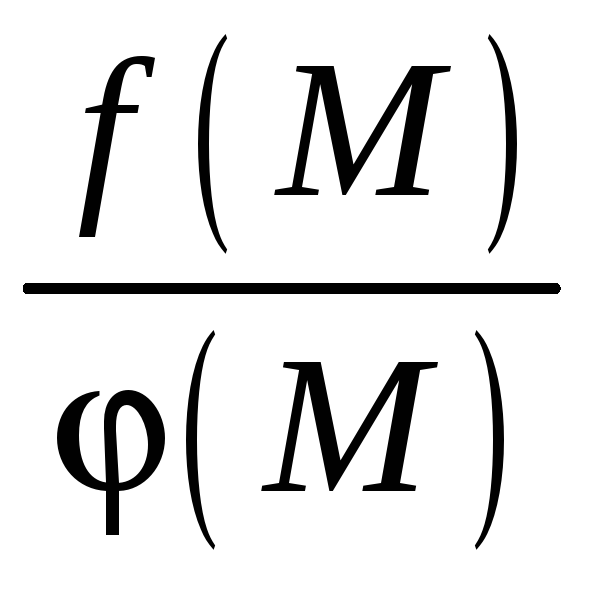 ;
;![]() или
или
![]() предел может существовать или не
существовать. В пределах такого типа,
требуются дополнительные преобразования
или специальные исследования. Рассмотрим
некоторые из них.
предел может существовать или не
существовать. В пределах такого типа,
требуются дополнительные преобразования
или специальные исследования. Рассмотрим
некоторые из них.
I.
Требуется найти предел дробно-рационального
выражения вида
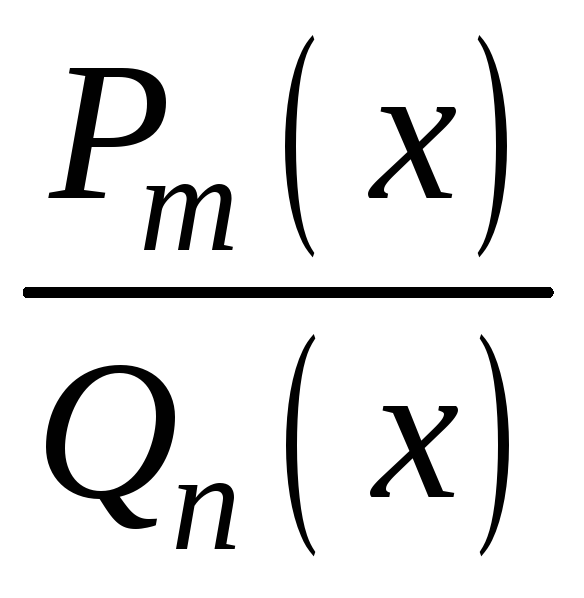 (отношение двух многочленов) при
(отношение двух многочленов) при
![]() ,
тогда в пределе будет иметь место
неопределенность
,
тогда в пределе будет иметь место
неопределенность
![]() .
Чтобы раскрыть её,
необходимо числитель
и знаменатель дроби разделить на
переменную в наибольшей степени.
.
Чтобы раскрыть её,
необходимо числитель
и знаменатель дроби разделить на
переменную в наибольшей степени.
Пример.
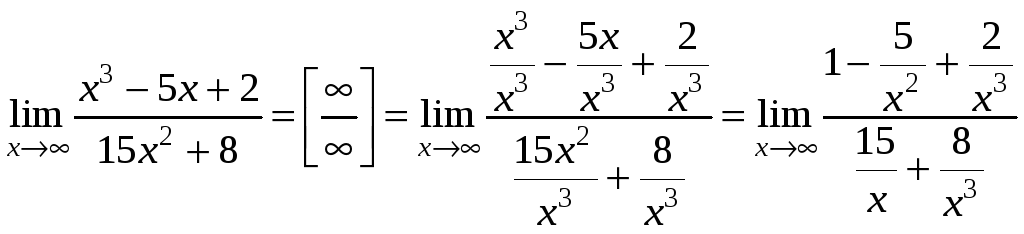 .
.
Предел числителя
равен
![]() ,
а знаменатель при
,
а знаменатель при
![]() сумма бесконечно малых величин, т.е.
величина бесконечно малая, поэтому вся
дробь – есть бесконечно большая величина,
т.е.
сумма бесконечно малых величин, т.е.
величина бесконечно малая, поэтому вся
дробь – есть бесконечно большая величина,
т.е.
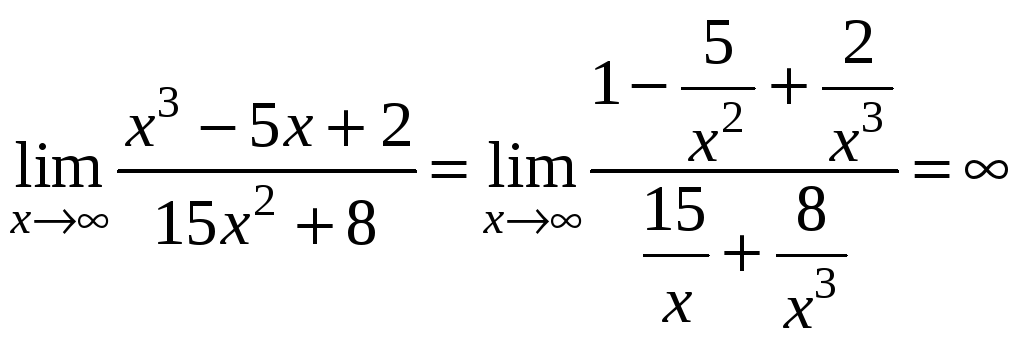 .
.
Пользуясь
рассмотренным выше способом можно
вывести правило
раскрытия неопределенности
![]() в пределе
отношения двух многочленов
в пределе
отношения двух многочленов
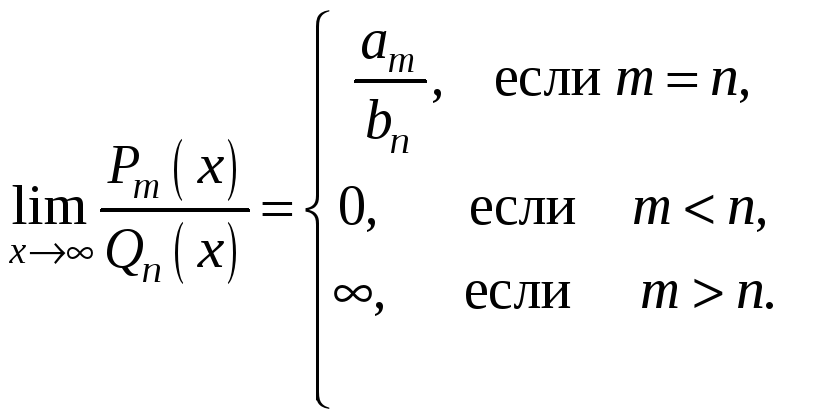
Пример.
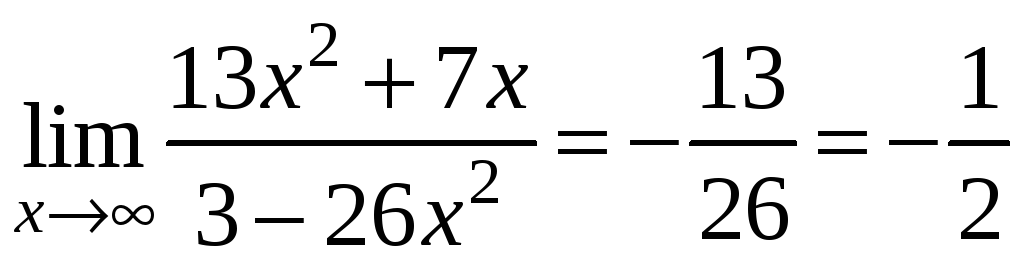 ,
так как
,
так как
![]() и
и
![]() ,
,
![]() .
.
II.
Пусть
требуется найти предел дроби, числитель
и знаменатель которой стремятся к нулю
при
![]() ,
тогда в пределе будет иметь место
неопределенность
,
тогда в пределе будет иметь место
неопределенность
![]() .
.
а) Если числитель и знаменатель – многочлены, то чтобы раскрыть данную неопределенность, необходимо числитель и знаменатель разложить на множители и сократить дробь.
В некоторых случаях
удобнее разделить числитель и знаменатель
на критический множитель
![]() (для функции одной переменной), или
воспользоваться определением предела.
(для функции одной переменной), или
воспользоваться определением предела.
Примеры.
1.
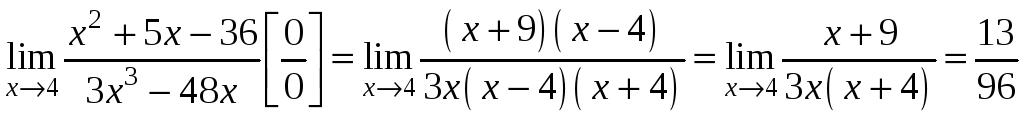 (при сокращении на
(при сокращении на
![]() учитывается, что
учитывается, что
![]() ,
но
,
но
![]() ).
).
2.
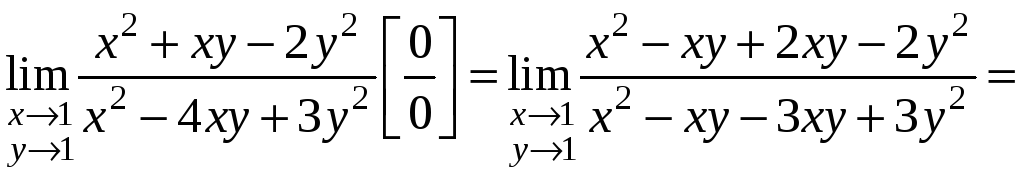
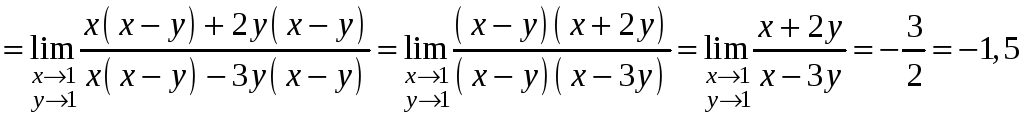
3.
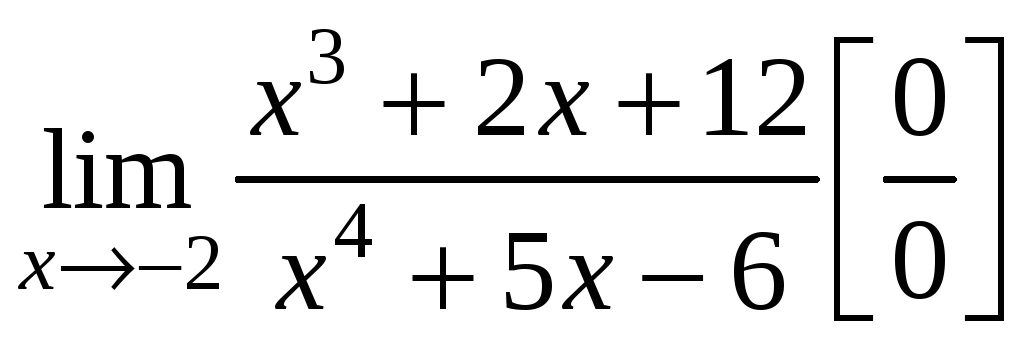 .
Разделим числитель и знаменатель на
критический множитель
.
Разделим числитель и знаменатель на
критический множитель
![]() :
:
Тогда
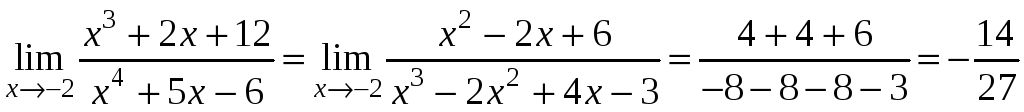 .
.
4.
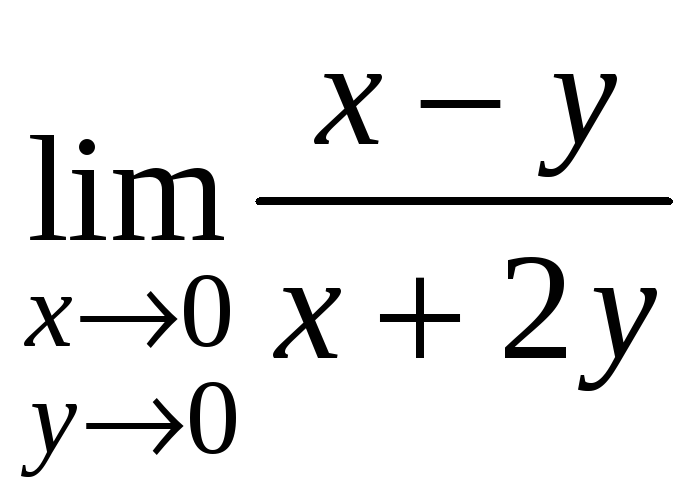 .
Будем приближаться к началу координат
по прямым
.
Будем приближаться к началу координат
по прямым
![]() ,
тогда
,
тогда
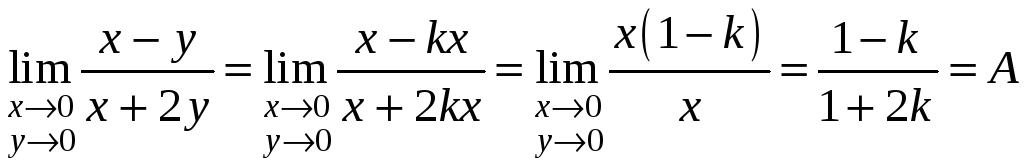 .
Имеем при
.
Имеем при
![]() ;
при
;
при
![]() ;
при
;
при
![]() и т.д. Отсюда следует, что предел этой
функции не существует.
и т.д. Отсюда следует, что предел этой
функции не существует.
b) Если дробь является иррациональным выражением, в некоторых случаях, чтобы раскрыть данную неопределенность необходимо числитель и знаменатель дроби умножить на выражение, сопряженное иррациональному или применить подстановку.
Примеры.
1.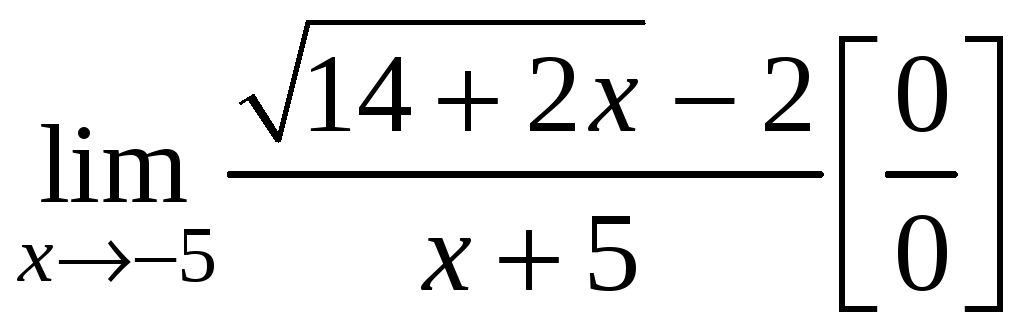 .
Умножим числитель и знаменатель на
выражение
.
Умножим числитель и знаменатель на
выражение
![]() – сопряженное числителю
– сопряженное числителю
![]() .
.
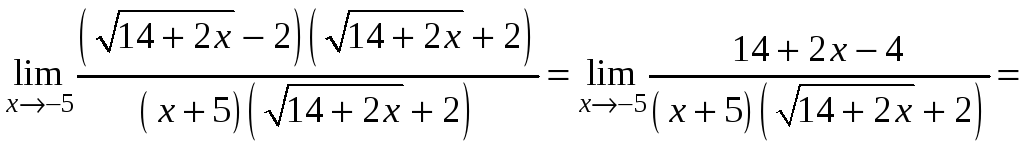
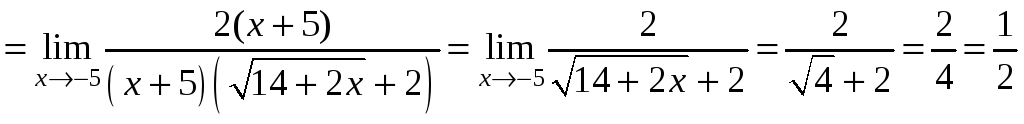 ,
таким образом
,
таким образом
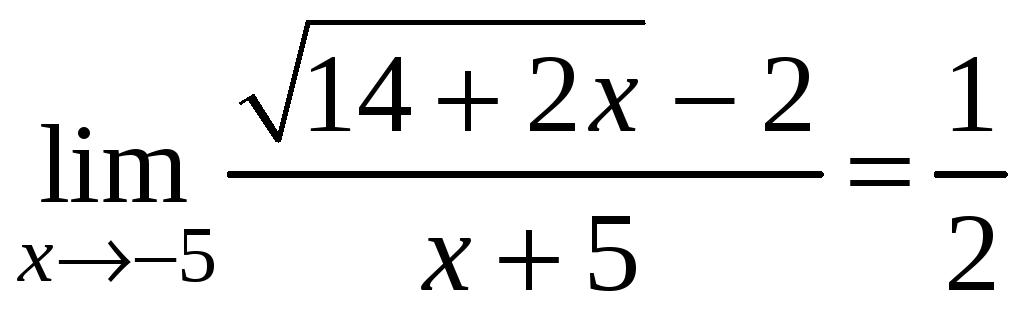 .
.
2.
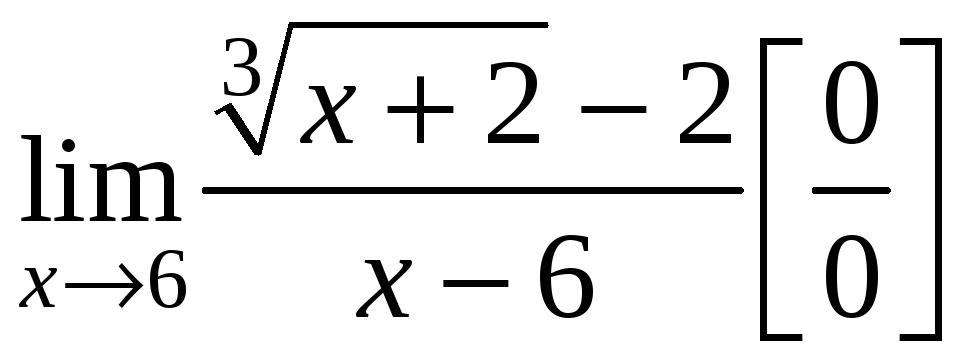 .
Выполним подстановку
.
Выполним подстановку
![]()
![]() при
при
![]()
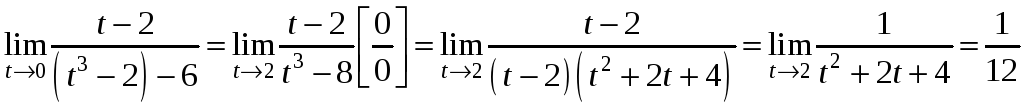 .
.
Таким образом,
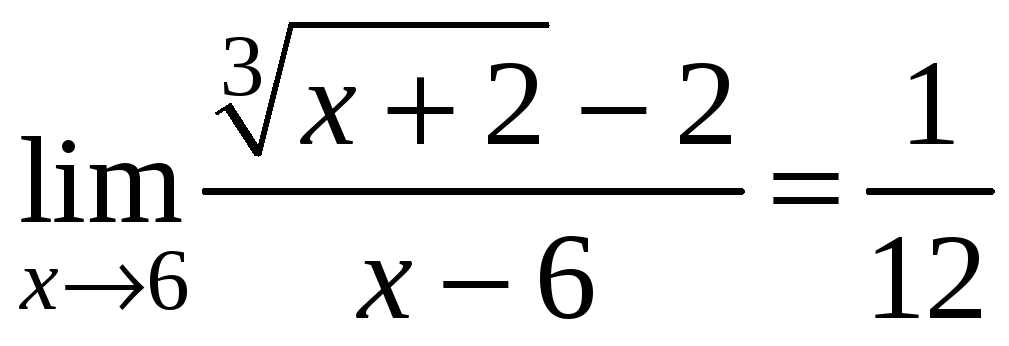 .
.
