
- •Раздел 2. Дифференциальное исчисление 138
- •Раздел 2. Дифференциальное исчисление лекция 2.1. Множества. Операции над множествами. Отображение множеств. Мощность множества. Множество действительных чисел
- •2.1.1. Множества. Операции над множествами. Отображение множеств
- •Свойства.
- •2.1.2. Множество действительных чисел
- •Лекция 2.2. Переменная величина. Функция одной и нескольких переменных. Способы задания. Основные элементарные функции, их свойства и графики
- •2.2.1. Переменная величина
- •2.2.2. Функция одной и нескольких переменных
- •2.2.3. Способы задания функции
- •2.2.4. Основные свойства функции
- •2.2.5. Классификация функций. Основные элементарные функции, их свойства и графики
- •Основные элементарные функции
- •Лекция 2.3. Предел переменной величины. Предел последовательности. Предел функции в точке. Бесконечно малые и бесконечно большие функции
- •2.3.1. Предел переменной величины.
- •2.3.2. Предел функции
- •2.3.3.Бесконечно малая и бесконечно большая функции, их свойства
- •Лекция 2.4. Теоремы о пределах и их применение. Признаки существования пределов
- •2.4.1. Теоремы о пределах
- •2.4.2. Признаки существования пределов
- •Лекция 2.5. Первый замечательный предел. Второй замечательный предел. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •2.5.1. Первый замечательный предел
- •2.5.2. Второй замечательный предел
- •2.5.3. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •Лекция 2.6. Приращение функции одной и двух переменных. Непрерывность функции одной и двух переменных. Точки разрыва
- •2.6.1. Приращение функции одной и двух переменных
- •2.6.2. Непрерывность функции одной и двух переменных
- •2.6.3. Точки разрыва
Лекция 2.6. Приращение функции одной и двух переменных. Непрерывность функции одной и двух переменных. Точки разрыва
2.6.1. Приращение функции одной и двух переменных
Рассмотрим
![]() функцию одной переменной, определенную
на некотором отрезке
функцию одной переменной, определенную
на некотором отрезке
![]() .
.
П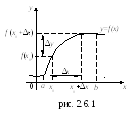 усть
некоторая точка
усть
некоторая точка
![]() и
и
![]() – значение функции в этой точке. Для
точки
– значение функции в этой точке. Для
точки
![]() зададим приращение
зададим приращение
![]() .
Тогда значение функции в новой точке
есть
.
Тогда значение функции в новой точке
есть
![]() .
Таким образом, функция получит приращение
.
Таким образом, функция получит приращение
![]() :
:
![]() (см. рис. 2.6.1).
(см. рис. 2.6.1).
![]() называется приращением
функции
называется приращением
функции
![]() в точке
в точке
![]() и может обозначаться
и может обозначаться
![]() .
.
![]() называется приращением
независимой переменной
или приращением
аргумента.
называется приращением
независимой переменной
или приращением
аргумента.
Рассмотрим
![]() – функцию двух переменных, определенную
на некоторой области
– функцию двух переменных, определенную
на некоторой области
![]() .
.
Так как функция
![]() зависит от двух переменных
зависит от двух переменных
![]() и
и
![]() ,
то приращение можно задать либо только
для одного из аргументов, либо для обоих
аргументов одновременно. В зависимости
от того скольким переменным задается
приращение, функция двух переменных
может получить либо частное,
либо полное
приращения.
,
то приращение можно задать либо только
для одного из аргументов, либо для обоих
аргументов одновременно. В зависимости
от того скольким переменным задается
приращение, функция двух переменных
может получить либо частное,
либо полное
приращения.
П усть
некоторая точка
усть
некоторая точка
![]() и
и
![]() – значение функции в этой точке. Зададим
приращение аргументу
– значение функции в этой точке. Зададим
приращение аргументу
![]() в точке
в точке
![]() :
:
![]() ,
оставляя
,
оставляя
![]() без изменения. Тогда значение функции
в новой точке
без изменения. Тогда значение функции
в новой точке
![]() есть
есть
![]() .
.
Т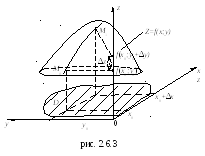
 аким
образом, функция получает частное
приращение по
аким
образом, функция получает частное
приращение по
![]() ,
которое обозначается
,
которое обозначается
![]() :
:
![]() (см. рис. 2.6.2)
(см. рис. 2.6.2)
Если задавать
приращение для аргумента
![]() равное
равное
![]() ,
оставляя при этом
,
оставляя при этом
![]() без изменения, то функция
без изменения, то функция
![]() получит частное
приращение
по
получит частное
приращение
по
![]() :
:
![]() (см. рис. 2.6.3).
(см. рис. 2.6.3).
Если задать
приращение одновременно для двух
аргументов –
![]() и
и
![]() ,
то функция
,
то функция
![]() получит полное
приращение:
получит полное
приращение:
![]() (см. рис. 2.6.4).
(см. рис. 2.6.4).
2.6.2. Непрерывность функции одной и двух переменных
Пусть
![]() – функция одной переменной. Рассмотрим
два определения непрерывности этой
функции в точке.
– функция одной переменной. Рассмотрим
два определения непрерывности этой
функции в точке.
Определение 1.
Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() ,
если эта функция определена в некоторой
окрестности точки
,
если эта функция определена в некоторой
окрестности точки
![]() и бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции, т. е.
и бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции, т. е.
![]() .
.
Пример.
Функция
![]() – непрерывна в любой точке
– непрерывна в любой точке
![]() .
.
Так как,
![]()
![]() ,
то
,
то
![]() .
А это и означает, что функция непрерывна.
.
А это и означает, что функция непрерывна.
Определение 2.
Функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если она определена в некоторой
окрестности этой точки, существуют
конечные односторонние пределы функции
в этой точке, которые равны между собой
и равны значению функции в точке
,
если она определена в некоторой
окрестности этой точки, существуют
конечные односторонние пределы функции
в этой точке, которые равны между собой
и равны значению функции в точке
![]() ,
т.е.
,
т.е.
![]()
![]() ,
где
,
где
![]() .
Иначе говоря, существует предел функции
.
Иначе говоря, существует предел функции
![]() в точке
в точке
![]() и он равен значению функции в этой точке.
и он равен значению функции в этой точке.
Определение.
Функция
![]() называется непрерывной
на интервале,
если она непрерывна в каждой его точке.
называется непрерывной
на интервале,
если она непрерывна в каждой его точке.
Замечание. Все основные элементарные функции непрерывны в тех интервалах, в которых они определены.
Пусть
![]() – функция двух переменных.
– функция двух переменных.
Определение.
Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() ,
если она определена в некоторой
окрестности этой точки и если бесконечно
малым приращениям аргументов
,
если она определена в некоторой
окрестности этой точки и если бесконечно
малым приращениям аргументов
![]() и
и
![]() соответствует бесконечно малое приращение
функции –
соответствует бесконечно малое приращение
функции –
![]() ,
т.е.
,
т.е.
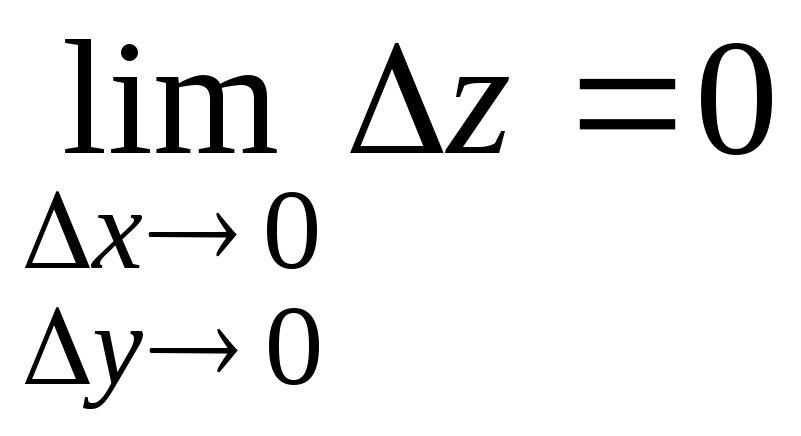 .
.
Определение.
Функция
![]() непрерывная в каждой точке области
называется непрерывной
в этой области.
непрерывная в каждой точке области
называется непрерывной
в этой области.
Сформулируем теоремы о непрерывных функциях, которые следуют непосредственно из соответствующих теорем о пределах (см. п. 2.4.1).
Теорема 1. Сумма, произведение конечного числа функций, непрерывных в некоторой точке, является функцией непрерывной в той же точке.
Теорема 2. Частное двух функций, непрерывных в некоторой точке, является функцией, непрерывной в той же точке, если знаменатель отличен от нуля.
Теорема 3. Сложная функция, составленная из конечного числа непрерывных функций, непрерывна.
Теорема 4. Функция, обратная к монотонной и непрерывной функции, непрерывна.
Непрерывность функции в замкнутом интервале обуславливает наличие у этой функции ряда важных свойств общего характера. Укажем некоторые из них.
Теорема 5. Функция, непрерывная в замкнутом интервале, хотя бы в одной точке интервала принимает наибольшее значение и хотя бы в одной – наименьшее.
Теорема 6. Функция, непрерывная в замкнутом интервале и принимающая на концах этого интервала значения разных знаков, хотя бы один раз обращается в ноль внутри интервала.
Теорема 7. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Теорема 8.
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и принимает на его концах неравные
значения
и принимает на его концах неравные
значения
![]() и
и
![]() ,
то на этом отрезке она принимает и все
промежуточные значения между
,
то на этом отрезке она принимает и все
промежуточные значения между
![]() и
и
![]() .
.
Приведенные
свойства можно перенести на функцию
любого числа переменных, непрерывную
в замкнутой области
![]() .
.
