
- •Раздел 2. Дифференциальное исчисление 138
- •Раздел 2. Дифференциальное исчисление лекция 2.1. Множества. Операции над множествами. Отображение множеств. Мощность множества. Множество действительных чисел
- •2.1.1. Множества. Операции над множествами. Отображение множеств
- •Свойства.
- •2.1.2. Множество действительных чисел
- •Лекция 2.2. Переменная величина. Функция одной и нескольких переменных. Способы задания. Основные элементарные функции, их свойства и графики
- •2.2.1. Переменная величина
- •2.2.2. Функция одной и нескольких переменных
- •2.2.3. Способы задания функции
- •2.2.4. Основные свойства функции
- •2.2.5. Классификация функций. Основные элементарные функции, их свойства и графики
- •Основные элементарные функции
- •Лекция 2.3. Предел переменной величины. Предел последовательности. Предел функции в точке. Бесконечно малые и бесконечно большие функции
- •2.3.1. Предел переменной величины.
- •2.3.2. Предел функции
- •2.3.3.Бесконечно малая и бесконечно большая функции, их свойства
- •Лекция 2.4. Теоремы о пределах и их применение. Признаки существования пределов
- •2.4.1. Теоремы о пределах
- •2.4.2. Признаки существования пределов
- •Лекция 2.5. Первый замечательный предел. Второй замечательный предел. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •2.5.1. Первый замечательный предел
- •2.5.2. Второй замечательный предел
- •2.5.3. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •Лекция 2.6. Приращение функции одной и двух переменных. Непрерывность функции одной и двух переменных. Точки разрыва
- •2.6.1. Приращение функции одной и двух переменных
- •2.6.2. Непрерывность функции одной и двух переменных
- •2.6.3. Точки разрыва
2.5.3. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
При приближении к предельной точке, общей для нескольких бесконечно малых функций, скорость их стремления к нулю бывает различной. Сравнение таких бесконечно малых функций привело к понятию порядка малости.
Если
![]() – бесконечно малая величина в окрестности
точки
– бесконечно малая величина в окрестности
точки
![]() ,
т.е.
,
т.е.
![]() ,
то
,
то
![]() – бесконечно малая функция
– бесконечно малая функция
![]() –го
порядка малости.
–го
порядка малости.
Чем выше порядок малости, тем быстрее переменная стремится к нулю.
Чтобы сравнить две бесконечно малые функции надо найти предел их отношения.
Пусть
![]() и
и
![]() есть бесконечно малые функции при
есть бесконечно малые функции при
![]() ,
т. е.
,
т. е.
![]() и
и
![]() .
.
1. Если
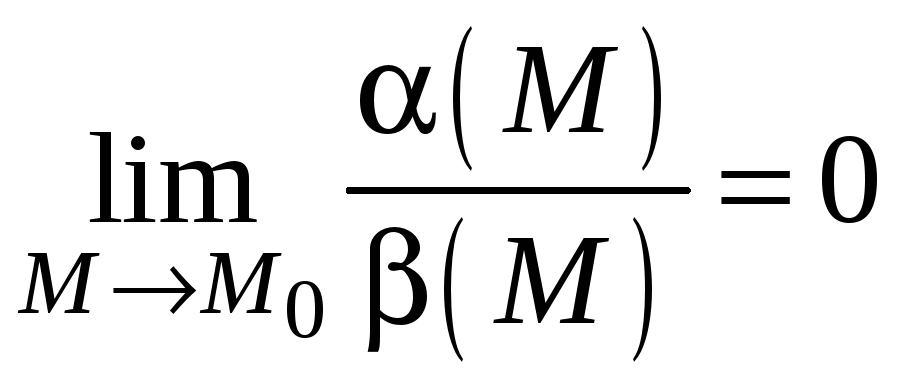 ,
то при
,
то при
![]()
![]() быстрее, чем
быстрее, чем
![]() ,
поэтому
,
поэтому
![]() – бесконечно
малая,
более высокого порядка малости.
– бесконечно
малая,
более высокого порядка малости.
2. Если
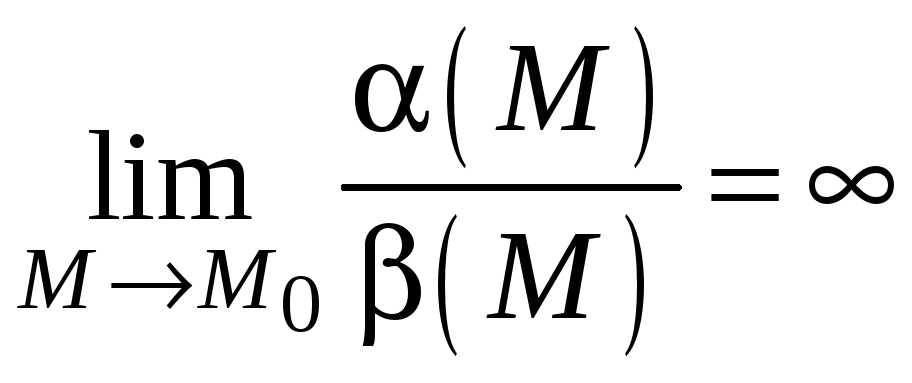 ,
то при
,
то при
![]()
![]() быстрее, чем
быстрее, чем
![]() ,
поэтому
,
поэтому
![]() – бесконечно
малая,
более высокого порядка малости.
– бесконечно
малая,
более высокого порядка малости.
3. Если
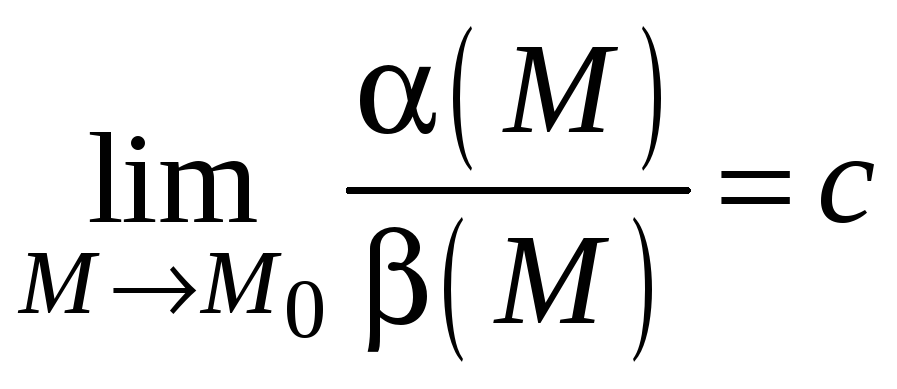 ,
то
,
то
![]() и
и
![]() – бесконечно
малые одного порядка малости.
– бесконечно
малые одного порядка малости.
4. Если
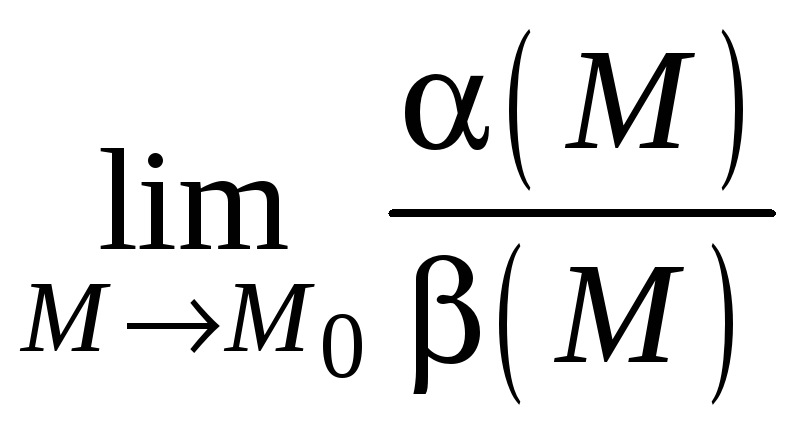 не существует, то
не существует, то
![]() и
и
![]() – несравнимые
бесконечно малые.
– несравнимые
бесконечно малые.
Отметим, что таковы
же правила сравнения бесконечно малых
функций при
![]() .
.
Примеры.
1. Сравнить
порядок функций
![]() и
и
![]() при
при
![]() .
.
Решение:
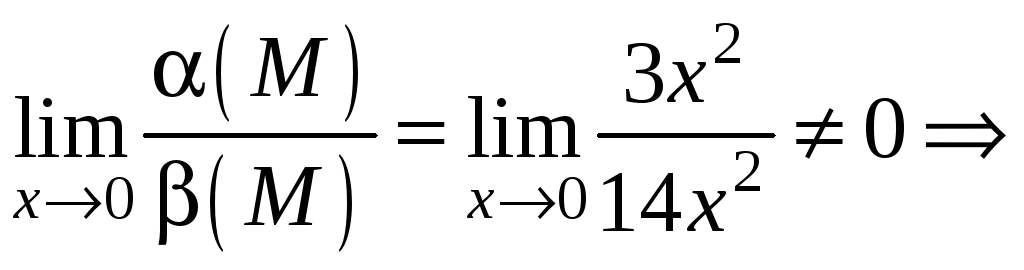
![]() и
и
![]() бесконечно малые функции одного порядка
при
бесконечно малые функции одного порядка
при
![]() .
.
2.
Сравнить порядок функций
![]() и
и
![]() при
при
![]() .
.
Решение:
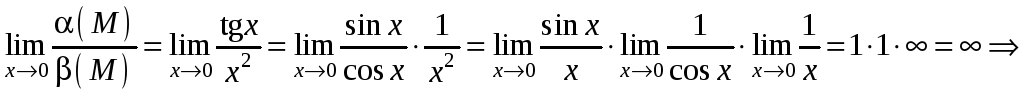
![]() – бесконечно малая
более высокого порядка.
– бесконечно малая
более высокого порядка.
3.
Можно ли сравнить функции
![]() и
и
![]() при
при
![]() ?
?
Решение:
Рассмотрим
передел
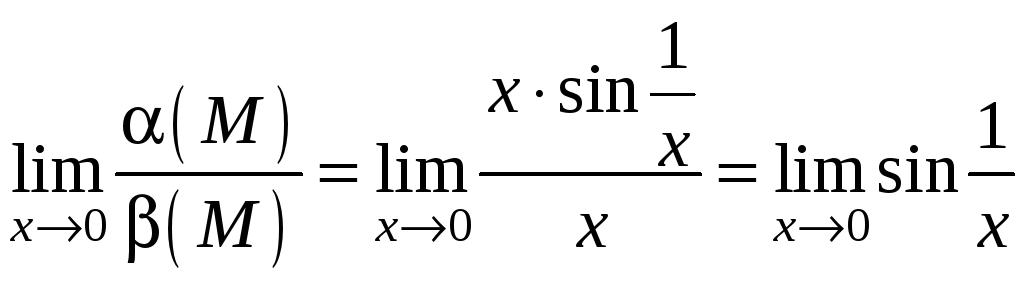 .
Этот предел не существует при
.
Этот предел не существует при
![]() функции
функции
![]() и
и
![]() при
при
![]() являются несравнимыми бесконечно малыми
функциями.
являются несравнимыми бесконечно малыми
функциями.
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые функции.
Определение.
Бесконечно малые функции
![]() и
и
![]() называются эквивалентными
при
называются эквивалентными
при
![]() ,
если
,
если
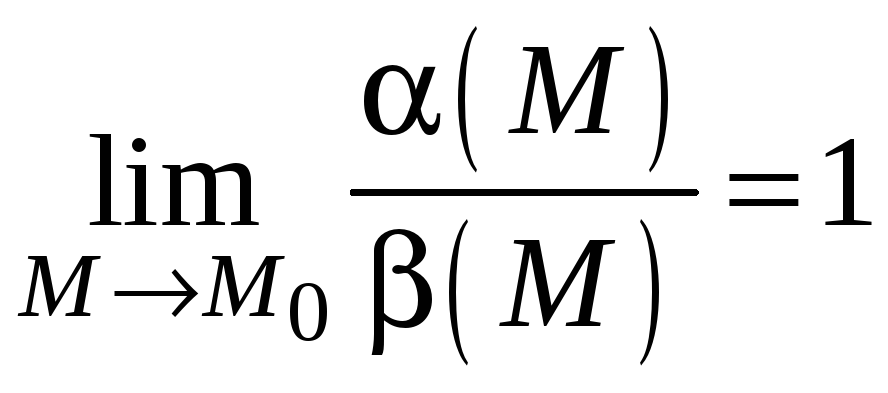 ;
это обозначается так:
;
это обозначается так:
![]() .
.
Пример.
![]() при
при
![]() ,
так как
,
так как
![]() ;
;
![]() при
при
![]() ,
так как
,
так как
![]() .
.
Теорема 8. Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
Доказательство:
Пусть
![]() и
и
![]() при
при
![]() .
Тогда
.
Тогда
 ,
т.е.
,
т.е.
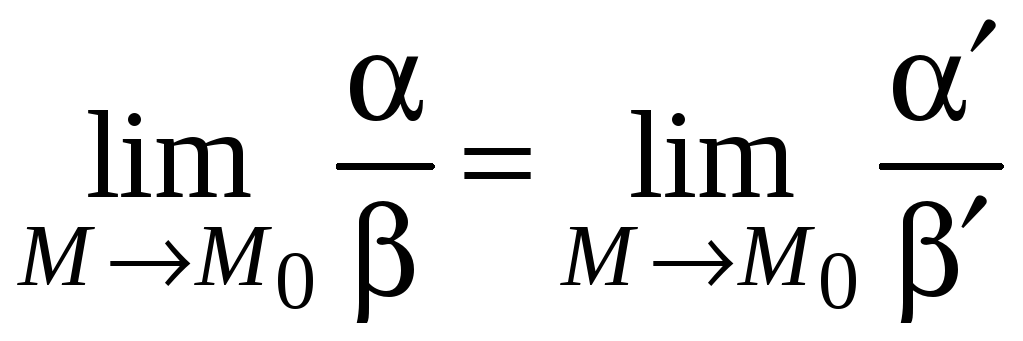 .
Ч.
и т.
д.
.
Ч.
и т.
д.
Очевидно также,
что
 .
.
Теорема 9. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая их них.
Теорема 10
(обратная). Если
разность бесконечно малых функций
![]() и
и
![]() есть бесконечно малая более высокого
порядка малости, чем
есть бесконечно малая более высокого
порядка малости, чем
![]() или
или
![]() ,
то
,
то
![]() и
и
![]() – эквивалентные бесконечно малые.
– эквивалентные бесконечно малые.
Терема 11. Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Доказательство:
Докажем
теорему для двух функций. Пусть
![]() ,
,
![]() при
при
![]() ,
причем
,
причем
![]() – бесконечно малая функция большего
порядка малости, чем
– бесконечно малая функция большего
порядка малости, чем
![]() ,
т.е.
,
т.е.
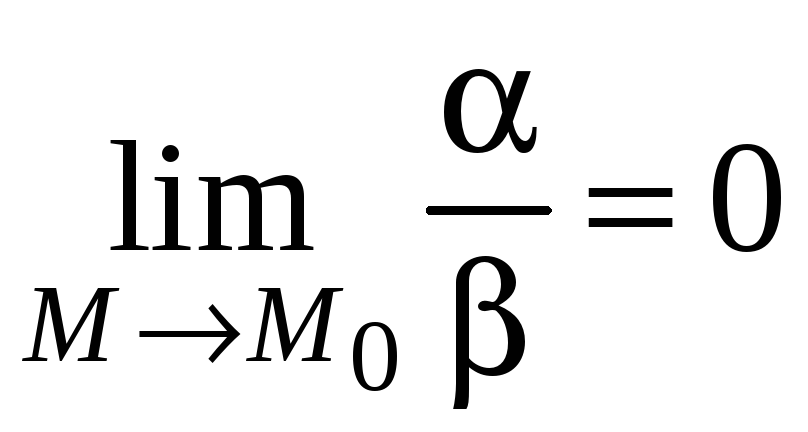 .
.
Тогда
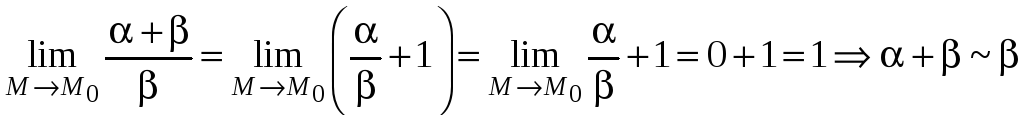 при
при
![]() .
.
Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы.
Замена суммы бесконечно малых величин её главной частью называется отбрасыванием бесконечно малых высшего порядка.
Пример.
Найти предел
![]() .
.
Решение:
Так как
![]() ,
а
,
а
![]() (так как
(так как
![]() – бесконечно малая функция более низкого
порядка малости чем
– бесконечно малая функция более низкого
порядка малости чем
![]() )
при
)
при
![]() (см. теорему 11), то
(см. теорему 11), то
![]() .
.
Для раскрытия
неопределенностей вида
![]() часто бывает полезным применять принцип
замены бесконечно малых эквивалентными
и другие свойства эквивалентных
бесконечно малых функций.
часто бывает полезным применять принцип
замены бесконечно малых эквивалентными
и другие свойства эквивалентных
бесконечно малых функций.
Известно, что
![]() при
при
![]() ,
,
![]() при
при
![]() .
Приведем еще примеры эквивалентных
бесконечно малых функций.
.
Приведем еще примеры эквивалентных
бесконечно малых функций.
Примеры.
1. Найдем
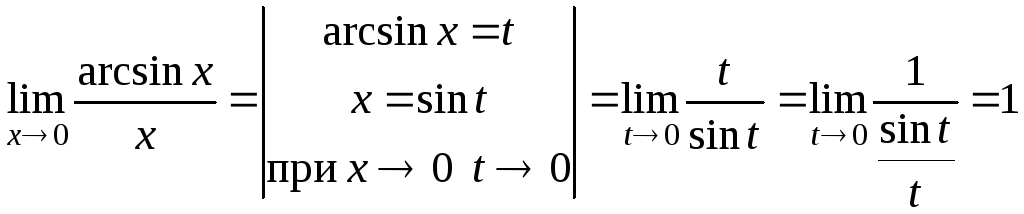 .
.
Следовательно,
![]() при
при
![]() .
.
2. Покажем,
что
![]() при
при
![]() .
.
Т.е. докажем, что
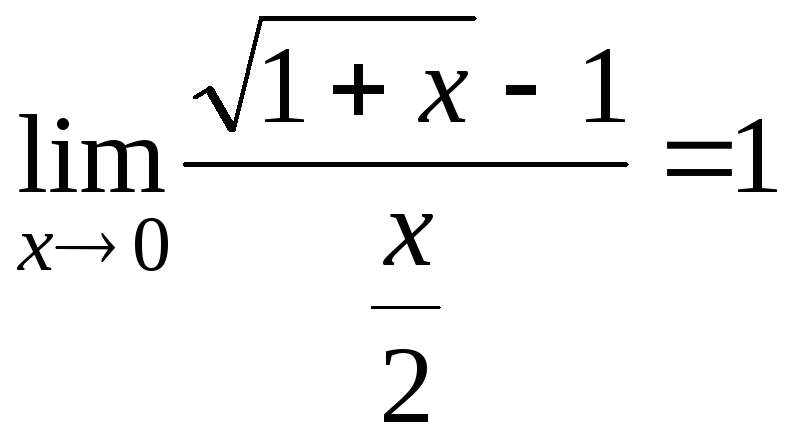 .
Действительно,
.
Действительно,
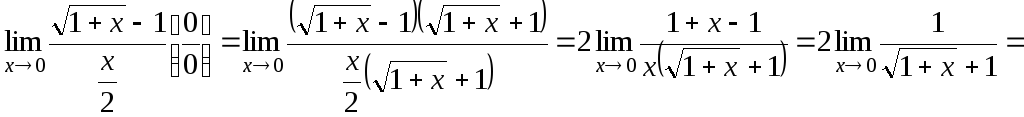
![]() .
Ч.
и т.
д. Значит,
.
Ч.
и т.
д. Значит,
![]() при
при
![]() .
.
Важнейшие эквивалентности приведены ниже:
при
![]()
|
1.
|
6.
|
|
2.
|
7.
|
|
3.
|
8.
|
|
4.
|
9.
|
|
5.
|
10.
в
частности,
|
Примеры.
1. Найти
![]() .
.
Решение:
При
![]()
![]() ,
,
![]() ,
тогда
,
тогда
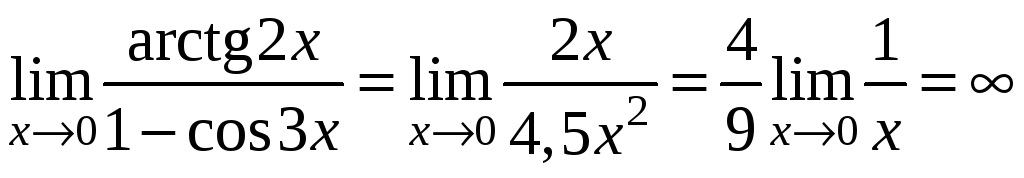
2. Найти
![]() .
.
Решение:
При
![]()
![]() ,
тогда
,
тогда
![]() .
Получаем
.
Получаем
![]() .
.
3. Найти
![]() .
.
Решение:
При
![]()
![]() ,
тогда
,
тогда
![]() .
.
