
- •Раздел 2. Дифференциальное исчисление 138
- •Раздел 2. Дифференциальное исчисление лекция 2.1. Множества. Операции над множествами. Отображение множеств. Мощность множества. Множество действительных чисел
- •2.1.1. Множества. Операции над множествами. Отображение множеств
- •Свойства.
- •2.1.2. Множество действительных чисел
- •Лекция 2.2. Переменная величина. Функция одной и нескольких переменных. Способы задания. Основные элементарные функции, их свойства и графики
- •2.2.1. Переменная величина
- •2.2.2. Функция одной и нескольких переменных
- •2.2.3. Способы задания функции
- •2.2.4. Основные свойства функции
- •2.2.5. Классификация функций. Основные элементарные функции, их свойства и графики
- •Основные элементарные функции
- •Лекция 2.3. Предел переменной величины. Предел последовательности. Предел функции в точке. Бесконечно малые и бесконечно большие функции
- •2.3.1. Предел переменной величины.
- •2.3.2. Предел функции
- •2.3.3.Бесконечно малая и бесконечно большая функции, их свойства
- •Лекция 2.4. Теоремы о пределах и их применение. Признаки существования пределов
- •2.4.1. Теоремы о пределах
- •2.4.2. Признаки существования пределов
- •Лекция 2.5. Первый замечательный предел. Второй замечательный предел. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •2.5.1. Первый замечательный предел
- •2.5.2. Второй замечательный предел
- •2.5.3. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •Лекция 2.6. Приращение функции одной и двух переменных. Непрерывность функции одной и двух переменных. Точки разрыва
- •2.6.1. Приращение функции одной и двух переменных
- •2.6.2. Непрерывность функции одной и двух переменных
- •2.6.3. Точки разрыва
2.3.3.Бесконечно малая и бесконечно большая функции, их свойства
Определение.
Функция одной переменной
![]() называется бесконечно
большой при
называется бесконечно
большой при
![]() ,
если для любого сколь угодно большего
числа
,
если для любого сколь угодно большего
числа
![]() найдется число
найдется число
![]() такое, что для всех
такое, что для всех
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() ,
т. е.
,
т. е.
![]() .
.
Пример.
Функция
![]() есть бесконечно большая функция при
есть бесконечно большая функция при
![]() .
.
Если
![]() стремится к бесконечности при
стремится к бесконечности при
![]() и принимает лишь положительные значения,
то пишут
и принимает лишь положительные значения,
то пишут
![]() ;
если лишь отрицательные значения, то
;
если лишь отрицательные значения, то
![]() .
.
Аналогично можно
дать определение для функции
![]() – независимых переменных.
– независимых переменных.
Определение.
Функция
![]() называется бесконечно
большой при
называется бесконечно
большой при
![]() ,
если для любого сколь угодно большого
числа
,
если для любого сколь угодно большого
числа
![]() найдется такая
найдется такая
![]() –окрестность
точки
–окрестность
точки
![]() ,
для всех точек которой выполняется
неравенство
,
для всех точек которой выполняется
неравенство
![]() ,
т.е.
,
т.е.
![]() .
.
Пример.
Функция двух переменных
![]() в окрестности точки
в окрестности точки
![]() (начало координат) является бесконечно
большой функцией, так как
(начало координат) является бесконечно
большой функцией, так как
![]() (см. рис.2.3.4).
(см. рис.2.3.4).

Отметим, что функция
![]() может являться бесконечно большой
функцией только
в окрестности точки
может являться бесконечно большой
функцией только
в окрестности точки
![]() ;
в других частях области определения
она может быть ограниченной величиной.
;
в других частях области определения
она может быть ограниченной величиной.
Определение.
Функция одной переменной
![]() ,
заданная на всей числовой оси, называется
бесконечно
большой при
,
заданная на всей числовой оси, называется
бесконечно
большой при
![]() ,
если для любого сколь угодно большого
числа
,
если для любого сколь угодно большого
числа
![]() найдется такое число
найдется такое число
![]() ,
что для всех
,
что для всех
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() ,
т. е.
,
т. е.
![]() .
.
Пример.
![]() для
для
![]() есть бесконечно большая функция при
есть бесконечно большая функция при
![]() ,
т. е.
,
т. е.
![]() .
.
Аналогично, функция
![]() ,
заданная на всех точках
,
заданная на всех точках
![]() – мерного пространства, называется
бесконечно
большой при
– мерного пространства, называется
бесконечно
большой при
![]() ,
если
,
если
![]() .
.
Определение.
Функция одной переменной
![]() называется бесконечно
малой при
называется бесконечно
малой при
![]() ,
если
,
если
![]() ,
т. е. для любого сколь угодно малого
,
т. е. для любого сколь угодно малого
![]() найдется число
найдется число
![]() такое, что для всех
такое, что для всех
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() ,
т.е.
,
т.е.
![]() .
.
Аналогично
определяется бесконечно малая функция
при
![]() ,
,
![]() ,
,
![]() ,
,
![]() :
во всех этих случаях
:
во всех этих случаях
![]() .
.
Примеры.
1.
![]() – бесконечно малая при
– бесконечно малая при
![]() .
.
2.
![]() – бесконечно малая при
– бесконечно малая при
![]() .
.
3.
![]() – бесконечно малая при
– бесконечно малая при
![]() ,
,
![]() .
.
Определение.
Функция нескольких переменных
![]() называется бесконечно
малой
при
называется бесконечно
малой
при
![]() ,
если для любого сколь угодно малого
числа
,
если для любого сколь угодно малого
числа
![]() найдется такая
найдется такая
![]() – окрестность точки
– окрестность точки
![]() ,
для всех точек которой выполняется
неравенство
,
для всех точек которой выполняется
неравенство
![]() ,
т.е.
,
т.е.
![]() .
.
Пример.
Функция двух переменных
![]() – бесконечно малая функция в
– бесконечно малая функция в
![]() – окрестности точки
– окрестности точки
![]() ,
,
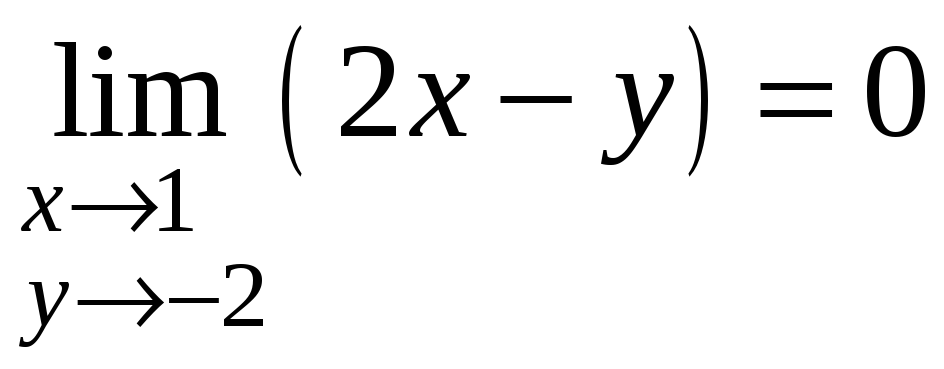 .
.
Функция любого числа переменных может быть бесконечно малой функцией только в окрестности предельной точки.
Пример.
Функция
![]() – бесконечно малая функция в окрестности
начала координат при
– бесконечно малая функция в окрестности
начала координат при
![]() и
и
![]() ,
а при бесконечном удалении от начала
координат по любому направлению при
,
а при бесконечном удалении от начала
координат по любому направлению при
![]() она неограниченно возрастает.
Следовательно, при
она неограниченно возрастает.
Следовательно, при
![]() она является бесконечно большой функцией.
она является бесконечно большой функцией.
Бесконечно малые
(большие) функции часто называют
бесконечно
малыми
(большими)
величинами,
их обозначают обычно греческими буквами
![]() ,
,![]() и т. д. или
и т. д. или
![]() .
.
Свойства бесконечно малой величины и её связь с бесконечно большой величиной сформулируем в виде теорем, и представим доказательства некоторых из них.
Теорема 3. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция, т.е.
если
![]() – бесконечно малая функция, где
– бесконечно малая функция, где
![]() ,
то
,
то
![]() – бесконечная функция.
– бесконечная функция.
Доказательство:
Пусть
![]() и
и
![]() две бесконечно малые функции
две бесконечно малые функции
![]() независимых переменных при
независимых переменных при
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
.
По определению
предела это значит, что для любого
![]() ,
а значит и
,
а значит и
![]() найдутся
найдутся
![]() –окрестность
и
–окрестность
и
![]() –окрестность
точки
–окрестность
точки
![]() ,
для всех точек которых будут соответственно
выполняться неравенства
,
для всех точек которых будут соответственно
выполняться неравенства
![]() и
и
![]() .
.
Пусть
![]() –наименьшее
из чисел
–наименьшее
из чисел
![]() и
и
![]() ,
тогда для всех точек из
,
тогда для всех точек из
![]() – окрестности будут выполняться оба
эти неравенства.
– окрестности будут выполняться оба
эти неравенства.
Следовательно, имеет место соотношение
![]() .
.
Это значит, что
![]() ,
т. е.
,
т. е.
![]() –бесконечно малая величина при
–бесконечно малая величина при
![]() .
Ч.
и т.
д.
.
Ч.
и т.
д.
Доказательство сохраняется, если вместо суммы двух бесконечно малых функций рассматривать их разность, а также в случае любого конечного числа бесконечно малых функций.
Теорема 4. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
Доказательство:
Если
![]() – бесконечно малая функция, а
– бесконечно малая функция, а
![]() – ограничена, то
– ограничена, то
![]() – бесконечно малая функция.
– бесконечно малая функция.
Доказательство проведем для функции одного неизвестного.
Рассмотрим функцию
![]() ,
которая ограничена при
,
которая ограничена при
![]() ,
тогда по определению ограниченной
функции (см. п.2.2.4) существует такое
,
тогда по определению ограниченной
функции (см. п.2.2.4) существует такое
![]() ,
что для всех
,
что для всех
![]() из
из
![]() –окрестности
точки
–окрестности
точки
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Пусть
![]() – бесконечно малая функция при
– бесконечно малая функция при
![]() ,
тогда для любого
,
тогда для любого
![]() ,
а значит, и
,
а значит, и
![]() найдется такая
найдется такая
![]() –окрестность
точки
–окрестность
точки
![]() ,
для всех точек которой выполняется
неравенство
,
для всех точек которой выполняется
неравенство
![]() .
.
Обозначим через
![]() наименьшее из чисел
наименьшее из чисел
![]() и
и
![]() ,
тогда для всех точек из
,
тогда для всех точек из
![]() – окрестности точки
– окрестности точки
![]() выполняются оба неравенства. Следовательно,
имеет место соотношение
выполняются оба неравенства. Следовательно,
имеет место соотношение
![]() .
.
Это значит, что
![]() ,
т. е.
,
т. е.
![]() – бесконечно малая функция.
– бесконечно малая функция.
Следствие 1. Произведение двух бесконечно малых функций есть функция бесконечно малая.
Следствие 2. Произведение числа (постоянной) и бесконечно малой величины есть функция бесконечно малая.
Теорема 5.
Частное от деления бесконечной малой
функции на функцию, имеющую предел
отличный от нуля, есть функция бесконечно
малая т.е. если
![]() – бесконечно малая функция и
– бесконечно малая функция и
![]() ,
то
,
то
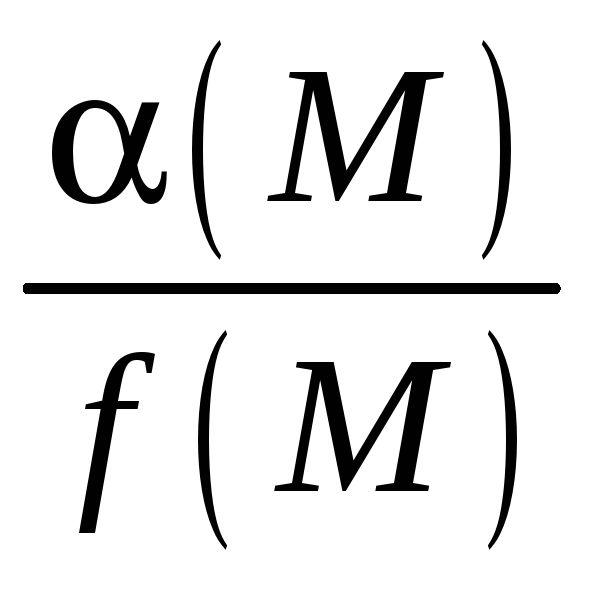 – бесконечно малая величина.
– бесконечно малая величина.
Теорема 6.
Если функция
![]() – бесконечно малая, то
– бесконечно малая, то
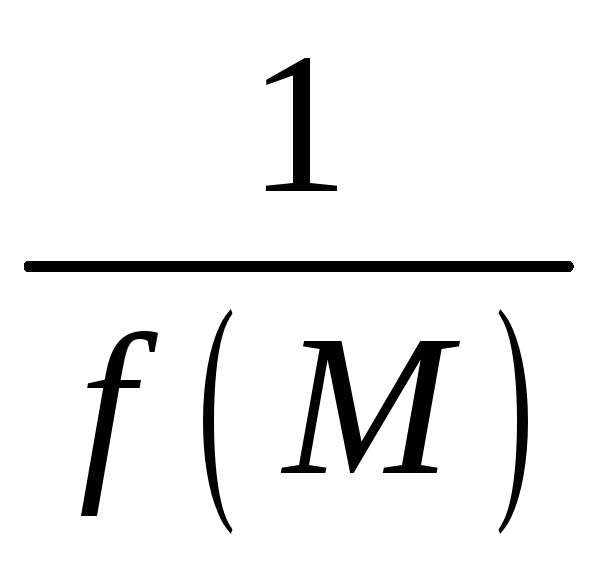 есть бесконечно большая функция и
наоборот: если
есть бесконечно большая функция и
наоборот: если
![]() – бесконечно большая функция, то
– бесконечно большая функция, то
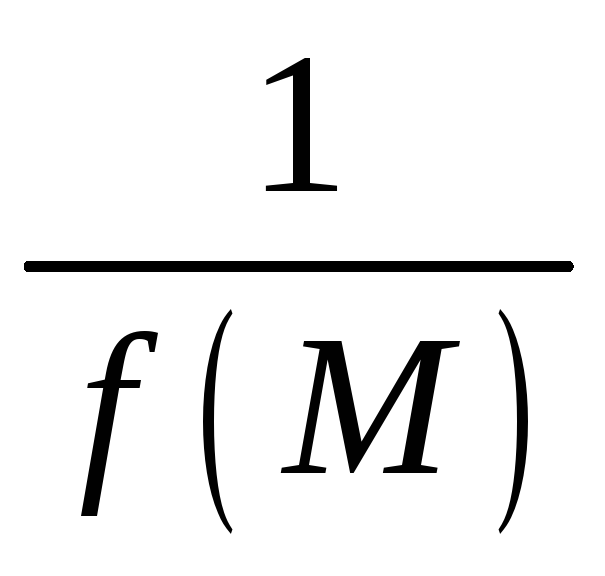 – бесконечно малая.
– бесконечно малая.
Доказательство:
Пусть
![]() – бесконечно малая функция при
– бесконечно малая функция при
![]() ,
т.е.
,
т.е.
![]() .
Тогда для любого
.
Тогда для любого
![]() найдется такая
найдется такая
![]() – окрестность точки
– окрестность точки
![]() ,
для всех точек которой выполняется
неравенство
,
для всех точек которой выполняется
неравенство
![]() .
.
Следовательно,
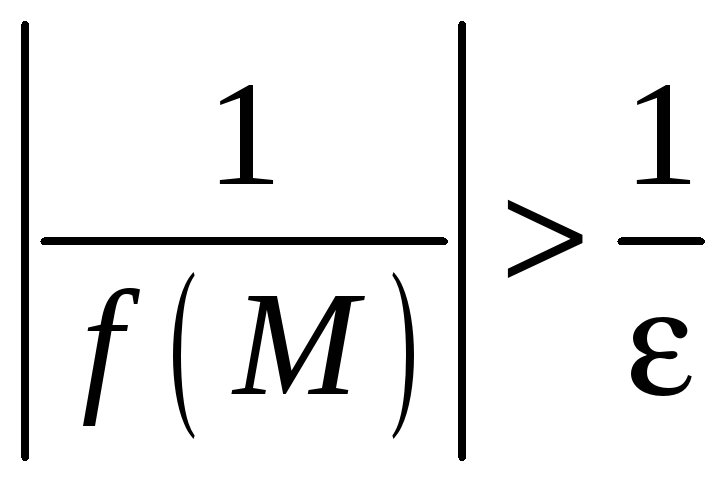 ,
т.е.
,
т.е.
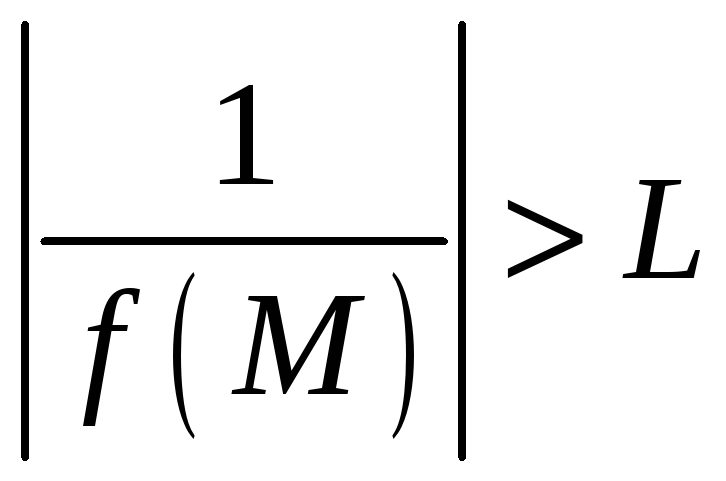 ,
где
,
где
![]() .
А это означает, что функция
.
А это означает, что функция
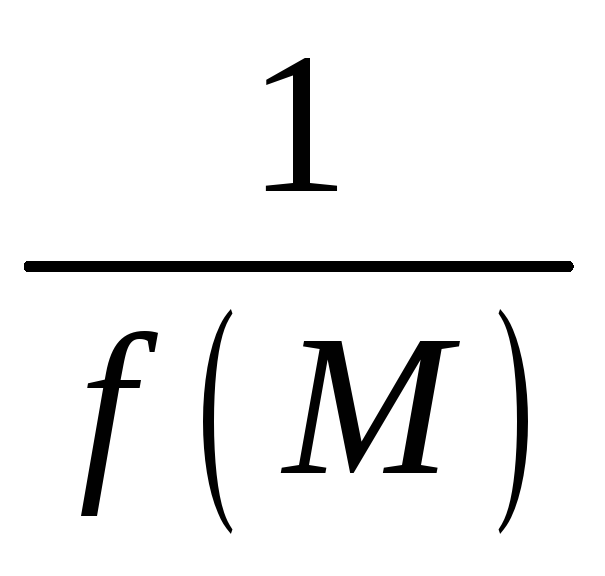 – есть бесконечно большая функция. Ч.
и т.
д.
– есть бесконечно большая функция. Ч.
и т.
д.
Аналогично доказывается обратное утверждение.
Замечание.
Доказательства теорем 3–6 приводились
для случая, когда
![]()
![]() ,
но они справедливы и для случая, когда
,
но они справедливы и для случая, когда
![]()
![]() .
.
Пример. Показать,
что функция
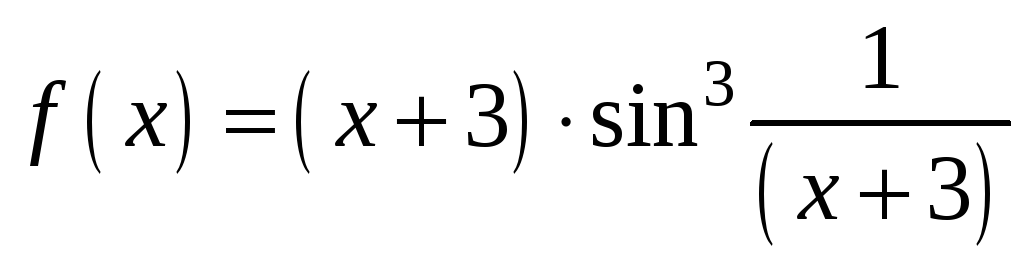 при
при
![]() является бесконечно малой.
является бесконечно малой.
Решение:
![]() функция
функция
![]() – бесконечно малая при
– бесконечно малая при
![]() .
.
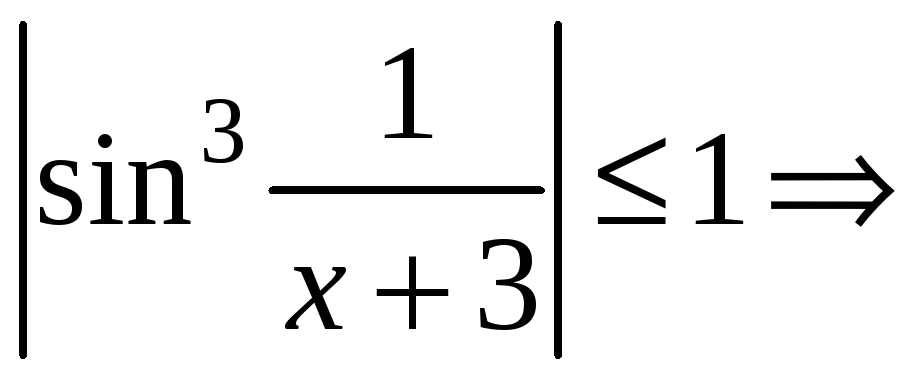 функция
функция
![]() ,
,
![]() ,
ограничена.
,
ограничена.
Таким образом,
функция
![]() – есть произведение бесконечной малой
и ограниченной функции. Значит по теореме
4 это функция бесконечно малая при
– есть произведение бесконечной малой
и ограниченной функции. Значит по теореме
4 это функция бесконечно малая при
![]() .
.
Рассмотрим теорему о связи между функцией, её пределом и бесконечно малой функцией.
Теорема 7.
Функция
![]() имеет предел равный
имеет предел равный
![]() тогда и только тогда , когда её можно
представить как сумму числа
тогда и только тогда , когда её можно
представить как сумму числа
![]() и бесконечно малой функции
и бесконечно малой функции
![]() ,
т.е.
,
т.е.![]() .
.
Доказательство:
Докажем прямое
утверждение: если
![]() ,
то
,
то
![]() .
.
Пусть
![]()
![]()
![]() точки
точки
![]() из
из
![]() – окрестности точки
– окрестности точки
![]() ,
т. е.
,
т. е.
![]() .
.
Это значит, что
![]() ,
т.е. что функция
,
т.е. что функция
![]() является бесконечно малой, которую
обозначим через
является бесконечно малой, которую
обозначим через
![]() ,
тогда
,
тогда
![]() .
Отсюда
.
Отсюда
![]() .
Ч.
и т.
д.
.
Ч.
и т.
д.
Докажем обратное
утверждение: если
![]() ,
то
,
то
![]() .
Пусть
.
Пусть
![]() ,
где
,
где
![]() – бесконечно малая функция при
– бесконечно малая функция при
![]() ,
т. е.
,
т. е.
![]()
![]()
![]() точки
точки
![]() из
из
![]() –окрестности
точки
–окрестности
точки
![]() .
.
По условию
![]() ,
то
,
то
![]() .
.
Получаем, что
![]()
![]()
![]() точки
точки
![]() из
из
![]() –окрестности
точки
–окрестности
точки
![]() .
.
А это и означает,
что
![]() .
Ч.
и т.
д.
.
Ч.
и т.
д.
