
- •Определение 4
- •Теорема 2
- •Теорема 5
- •Теорема 6
- •Теорема 7
- •Теорема 8
- •Определение 19
- •Теорема 9
- •Теорема 13 (о базисе в пространстве, на плоскости, на прямой)
- •Теорема 14
- •Теорема 18 (критерий коллинеарности)
- •Определение 39
- •Теорема 19 (критерий компланарности)
- •Определители Определение 40
- •Преобразование аффинной системы координат на плоскости
- •Определение 50
- •Различные способы задания прямой на плоскости
- •1) Нахождение угла между прямыми
- •2) Расстояние от точки до прямой
- •Плоскость в пространстве Определение 51
- •Теорема 23
- •Способы задания плоскости в пространстве
- •Определение 52
- •Прямая в пространстве
- •Определение 53
- •Определение 54
- •Определение 55
- •Кривые второго порядка Эллипс Определение 56
- •Определение 57
- •Определение 58
- •Свойства эллипса
- •Определение 59
- •Определение 60
- •Определение 61
- •Эксцентриситет и директриса
- •Определение 62
- •Определение 63
- •Уравнение эллипса в полярных координатах
- •Гипербола Определение 64
- •Определение 65
- •Свойства гиперболы
- •Определение 66
- •Определение 67
- •Определение 68
- •Полярное уравнение гиперболы
- •Парабола Определение 69
- •1 Случай
- •2 Случай
- •Теорема 25
- •Теорема 26
- •Цилиндрические поверхности Определение 79
- •Конические поверхности Определение 80
- •Определение 81
Парабола Определение 69
Параболой называется
множество точек плоскости, для которых
расстояния до фиксированной точки
![]() и до фиксированной прямой
и до фиксированной прямой
![]() равны. Точка
равны. Точка
![]() называется фокусом параболы, а прямая
называется фокусом параболы, а прямая
![]() - директрисой параболы.
- директрисой параболы.
Замечание
Если точка
![]() принадлежит прямой
принадлежит прямой
![]() ,
то множество таких точек – прямая,
перпендикулярная
,
то множество таких точек – прямая,
перпендикулярная
![]() и проходящая через
и проходящая через
![]() .
Поэтому будем считать, что
.
Поэтому будем считать, что
![]() .
.
Выберем систему координат:

Расстояние
![]() от
от
![]() до
до
![]() равно
равно
 .
Расстояние от
.
Расстояние от
![]() до фокуса
до фокуса
![]() равно
равно
 .
Так как
.
Так как
![]() ,
то
,
то

Проверим, что
каждая точка
![]() удовлетворяющая уравнению
удовлетворяющая уравнению
![]() принадлежит этой параболе. Расстояние
от точки
принадлежит этой параболе. Расстояние
от точки
![]() до
до
![]() равно
равно
 .
.
Расстояние от
точки
![]() до прямой
до прямой
![]() равно
равно
 .
Эти расстояния равны, значит точка
.
Эти расстояния равны, значит точка
![]() принадлежит параболе.
принадлежит параболе.
Определение 70
Уравнение вида
![]() (
(![]() )
называется каноническим уравнением
параболы.
)
называется каноническим уравнением
параболы.
Определение 71
Система координат, в которой парабола имеет каноническое уравнение, называется канонической системой координат.
Свойства параболы
1) Парабола имеет одну ось симметрии. Точка пересечения этой оси с параболой называется вершиной параболы.
2) Парабола не имеет центра симметрии.
Определение 72
Для параболы эксцентриситет полагают равным 1.
Полярное уравнение параболы.
Поместим начало
координат в фокус параболы
![]() .
Тогда расстояние до фокуса равно
.
Тогда расстояние до фокуса равно
![]() ,
а расстояние до директрисы равно
,
а расстояние до директрисы равно
![]() .
Эти два расстояния равны, т.е.
.
Эти два расстояния равны, т.е.
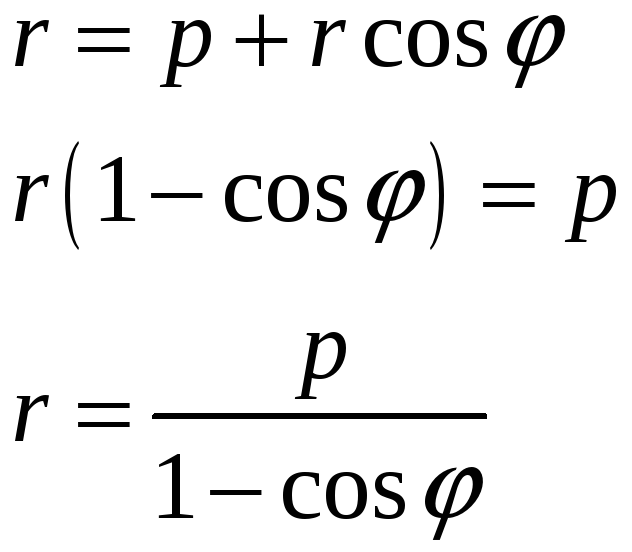
Теорема 24
Пусть на плоскости
заданы прямая
![]() и точка
и точка
![]() .
Тогда множество точек, для которых
отношение расстояний до точки
.
Тогда множество точек, для которых
отношение расстояний до точки
![]() и до прямой
и до прямой
![]() равно
равно
![]() является
является
1) эллипсом при
![]() ;
2)
гиперболой, при
;
2)
гиперболой, при
![]() ;
3)
параболой, при
;
3)
параболой, при
![]() .
.
Исследование уравнений второго порядка
Определение 73
Линией второго порядка называется линия, задаваемая в некоторой декартовой системе координат уравнением:
![]() ,
где
,
где
![]() .
.
Пусть в некоторой
декартовой системе координат линия
задана уравнением
![]() .
Найдем систему координат, в которой
линия задается более простым уравнением.
Для этого будем рассматривать переходы
от одной системы координат к другой
следующего вида:
.
Найдем систему координат, в которой
линия задается более простым уравнением.
Для этого будем рассматривать переходы
от одной системы координат к другой
следующего вида:
Поворот на угол
![]() :
:
 ,
,
![]() - координаты в новом базисе.
- координаты в новом базисе.
Перенос начала системы координат:

Посмотрим как меняется уравнение при повороте:


Выберем угол
поворота так, чтобы
![]() .
.

Если
![]() ,
то
,
то
![]() ,
Если
,
Если
![]() ,
то
,
то
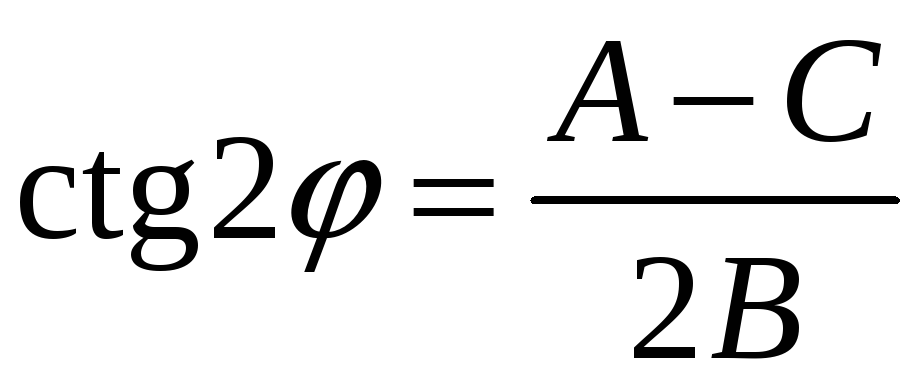 ,
т.е.
,
т.е.
 .
.
Далее можно найти
![]() и
и
![]() (
(![]() ).
).
При выбранном
![]() уравнение имеет вид
уравнение имеет вид
![]()
Перейдем к следующей системе координат посредством сдвига:

1 Случай
![]() (т.е.
(т.е.
![]() и
и
![]() )
)


Если
![]() (
(![]() ),
то
),
то

Так как
 и
и
 ,
то обозначим
,
то обозначим
 ,
а
,
а
 .
.
Получим уравнение
вида
 .
Это уравнение эллипса.
.
Это уравнение эллипса.
Если мы хотим
получить каноническое уравнение эллипса,
то требуется, чтобы коэффициент при
![]() был меньше, чем при
был меньше, чем при
![]() .
.
При
![]() можно сделать поворот системы координат
на
можно сделать поворот системы координат
на
![]() и получить каноническое уравнение
эллипса.
и получить каноническое уравнение
эллипса.
Если
![]() ,
то
,
то
 ,
где
,
где
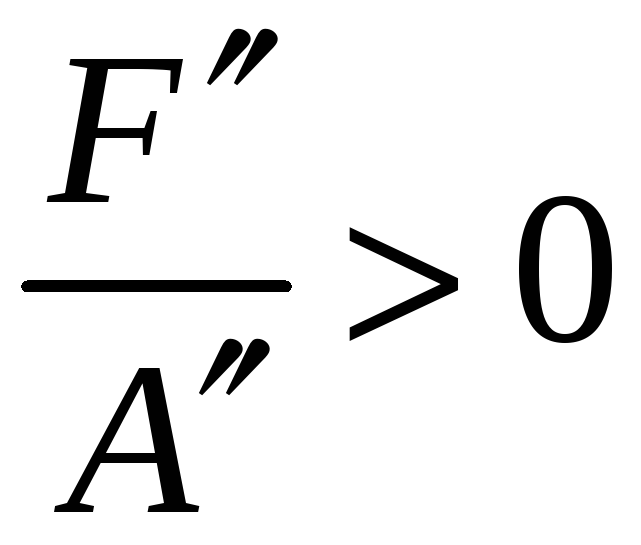 и
и
 .
.
Точек плоскости, удовлетворяющих этому уравнению, не существует. Говорят, что данное уравнение описывает мнимый эллипс.
Если
![]() и
и
![]() ,
то
,
то

Этому уравнению
удовлетворяет одна точка с координатами
![]() и
и
![]() .
Говорят, что данное уравнение описывает
вырожденный эллипс.
.
Говорят, что данное уравнение описывает
вырожденный эллипс.
Если
![]() и
и
![]() ,
то
,
то
 ,
где
либо
,
где
либо
 и
и
 ,
либо
,
либо
 и
и
 .
.
Если
 и
и
 ,
то, обозначив
,
то, обозначив
 и
и
 ,
получим уравнение
,
получим уравнение
 .
Это каноническое уравнение гиперболы.
.
Это каноническое уравнение гиперболы.
Если
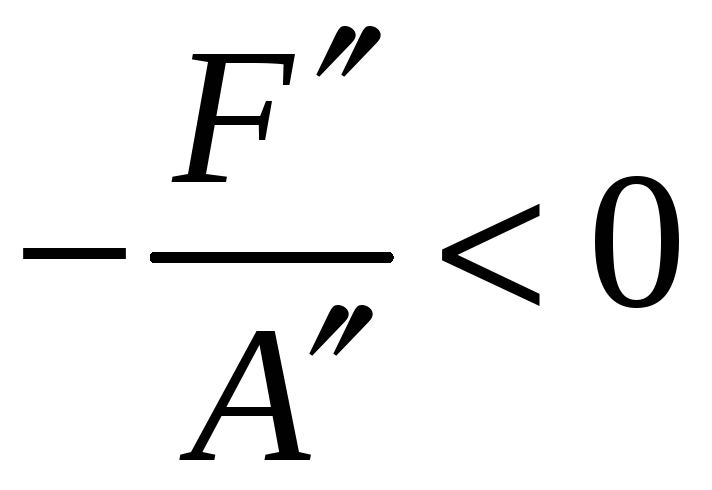 и
и
 ,
то обозначим
,
то обозначим
 и
и
 .
Получим уравнение
.
Получим уравнение
 .
Перейдем к новой системе координат
посредством поворота на угол
.
Перейдем к новой системе координат
посредством поворота на угол
![]() .
.

Получим уравнение
 .
Это тоже каноническое уравнение
гиперболы.
.
Это тоже каноническое уравнение
гиперболы.
Если
![]() и
и
![]() ,
то уравнение имеет вид
,
то уравнение имеет вид
 .
Обозначим
.
Обозначим
 ,
,
 .
Тогда
.
Тогда

Уравнение описывает пару пересекающихся прямых
 и
и
 .
Точка пересечения прямых
.
Точка пересечения прямых
![]() .
.
