Определение 50

Уравнения первого порядка будем называть линейными уравнениями.

Различные способы задания прямой на плоскости

1) Любая прямая на плоскости задается уравнением вида , где вектор с координатами является ортогональным к этой прямой. Это уравнение называется общим уравнением прямой на плоскости. Если и задают одну и ту же прямую, то .

2) Уравнение прямой, проходящий через точку , ортогональной вектору : .

3) Уравнение в отрезках. Если прямая задается полным уравнением, т.е. и и , то эквивалентно или .

4) Нормированное уравнение. Вектор с координатами имеет единичную длину. Обозначим , где и - направляющие косинусы. Получим , где .

Если обозначить 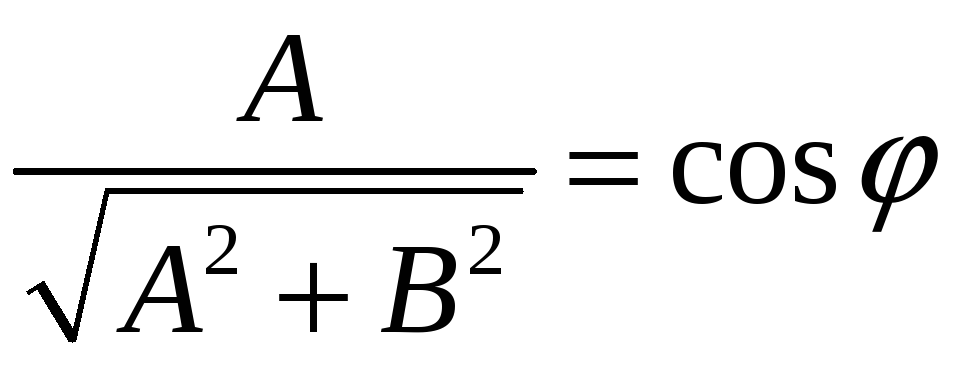, а , где - угол между векторами и , получим .

5) Каноническое уравнение. Пусть дано уравнение прямой , . Вектор с координатами ортогонален прямой. Вектор с координатами ортогонален вектору с координатами (так как ). Таким образом вектор с координатами является параллельным нашей прямой. Поэтому вектора с координатами и коллинеарны. По свойствам коллинеарных векторов . Получим: если вектор является параллельным прямой, то уравнение прямой .

6) Уравнение прямой, проходящей через две точки. Требуется написать уравнение прямой, проходящей через точки и . Вектор с координатами параллелен прямой. Поэтому уравнение прямой .

7) Параметрическое задание прямой. Пусть вектор с координатами параллелен прямой, проходящей через точку . Тогда для любой точки этой прямой с координатами вектор коллинеарен вектору : . Получаем

Задачи

1) Нахождение угла между прямыми

Пусть в декартовой системе координат две прямые заданы уравнениями и . Если , то эти прямые совпадают. Если , то эти прямые не имеют общих точек, т.е. параллельны. Пусть . Тогда прямые пересекаются. Так как вектор параллелен прямой и вектор параллелен прямой , то угол между векторам и совпадает с углом между векторами и , т.е. угол между прямыми совпадает с углом между перпендикулярными прямыми. 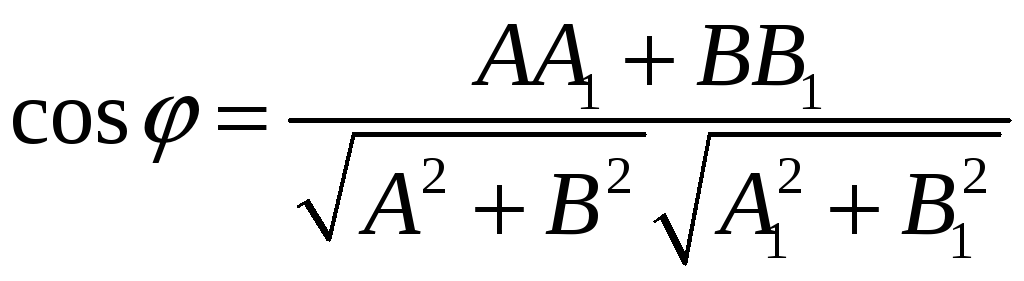Угол между перпендикулярами может быть найден по формуле , либо

2) Расстояние от точки до прямой

Пусть задано уравнение прямой и точка . Нормируем уравнение прямой: и пусть точка принадлежит прямой. Нормальный вектор к прямой , причем . Угол между вектором и обозначим через . Тогда расстояние от точки до прямой равно

Замечание

Если точка лежит по ту же сторону от прямой, куда направлен вектор , то угол - острый и величина . Если точка лежит по другую сторону от прямой, то угол - тупой и величина .

Задача

Построение биссектрисы угла между прямыми

Пусть даны уравнения прямых

По последнему замечанию для всех точек по одну сторону от первой прямой выражение имеет положительные значения, а по другую отрицательные. Аналогично для второй прямой. Поэтому произведение величин и сохраняет знак в вертикальных углах. Биссектриса угла обладает тем свойством, что каждая точка на биссектрисе равноудалена от прямых. Поэтому уравнения биссектрис

Переносим в левую сторону, и получаем

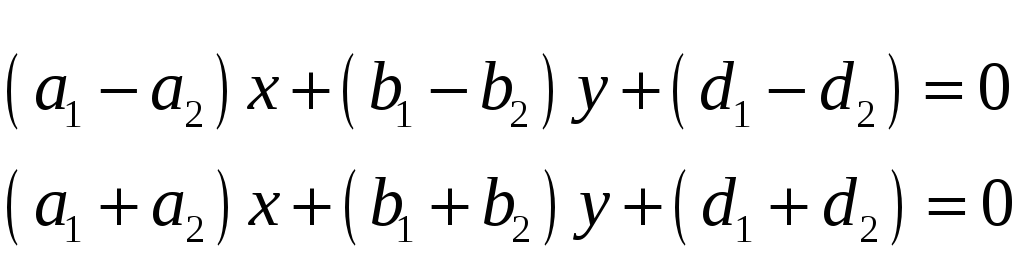
Плоскость в пространстве Определение 51

Плоскостью , проходящей через точку , ортогональной вектору называется множество точек таких, что ортогонален , т.е. . Если вектор имеет координаты , точка имеет координаты , то для точки с координатами получаем уравнение принадлежности плоскости или , где .