Определение 53

Углом между прямыми называется угол между направляющими векторами этих прямых. Направляющий вектор первой прямой имеет координаты , второй прямой . Угол между этими векторами

2) Условия на принадлежность прямых одной плоскости

Пусть прямые заданы уравнениями

Обозначим направляющий вектор с координатами через , вектор с координатами через . Обозначим . Если прямые параллельны, то через них можно провести плоскость и векторы компланарны. Если прямые пересекаются, то через них можно провести плоскость и векторы компланарны. Если прямые скрещивающиеся, то векторы некомпланарны. Таким образом условие принадлежности прямых одной плоскости записывается или в координатах:

3) Угол между прямой и плоскостью

Пусть плоскость задана уравнением , а прямая уравнением . Обозначим через вектор с координатами , через вектор с координатами . Угол между векторами и через , угол между прямой и плоскостью, через . Угол удовлетворяет неравенству . Поэтому

4) Нахождение проекции точки на плоскость

Определение 54

Проекцией точки на плоскость называется точка такая, что и .

Пусть плоскость задана уравнением , точка имеет координаты , - вектор с координатами .

Напишем параметрическое уравнение прямой, проходящей через точку перпендикулярно плоскости.

Точка лежит на этой прямой и принадлежит плоскости, поэтому ее координаты удовлетворяют уравнению

Координаты точки

5) Проекция точки на прямую

Определение 55

Проекцией точки на прямую называется точка такая, что и .

Пусть прямая задана уравнением . Направляющий вектор , точка . Уравнение плоскости, проходящей через точку , перпендикулярную прямой: . Точка , являющаяся пересечением плоскости и прямой, является проекцией точки на прямую и является проекцией точки на плоскость. Параметрическое уравнение прямой:

Подставляем в уравнение плоскости:

. Таким образом координаты точки :

6) Уравнение прямой, перпендикулярной двум скрещивающимся прямым

Пусть заданы прямые

Вектор перпендикулярен первой и второй прямой, значит он является направляющим вектором прямой, перпендикулярной скрещивающимся прямым. Плоскость, проходящая через искомую прямую и первую прямую задается уравнением , где - координаты вектора . Плоскость, проходящая через искомую прямую и вторую прямую задается уравнением , где - координаты вектора . Уравнение искомой прямой:

7) Расстояние между скрещивающимися прямыми в пространстве

Пусть прямые заданы уравнениями

- точка с координатами , - точка с координатами . Уравнение плоскости, проходящей через точку параллельно векторам и .

Расстояние от первой прямой до второй – это расстояние от до построенной плоскости:

8) Расстояние между параллельными плоскостями

Пусть плоскости заданы уравнениями

Пусть точка с координатами принадлежит первой плоскости, т.е. . Расстояние от первой плоскости до второй равно расстоянию от точки до второй плоскости. Оно равно .

Кривые второго порядка Эллипс Определение 56

Эллипсом называется множество точек сумма расстояний от каждой из которых до точек и постоянна. Точки и называются фокусами эллипса.

Замечание

Если точки и совпадают, то полученная фигура называется окружностью.

Обозначим фиксированную сумму через , а расстояние между и через . Если , то подходящих под определение точек на плоскости нет. Если , то получается отрезок. Будем считать, что .

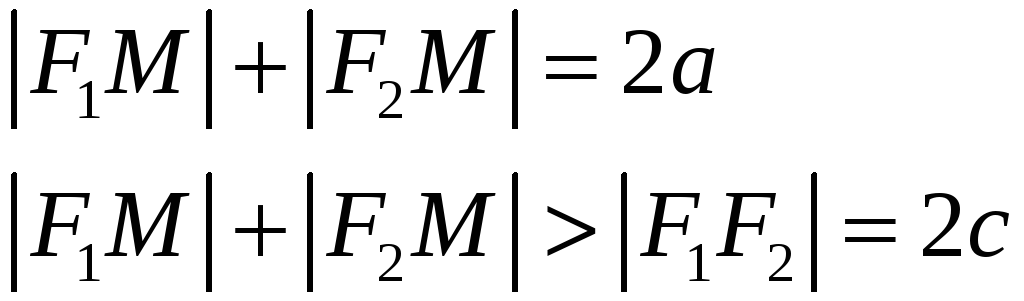
Введем декартову систему координат, в которой точка имеет координаты , а точка координаты .

Выведем уравнение эллипса. Пусть принадлежит эллипсу. Тогда

Проверим, что каждая точка удовлетворяющая этому уравнению принадлежит эллипсу. Пусть точка удовлетворяет уравнению

Докажем, что точка принадлежит эллипсу.

Из этого уравнения имеем . Расстояние от точки до фокуса равно

Так как удовлетворяет уравнению , то 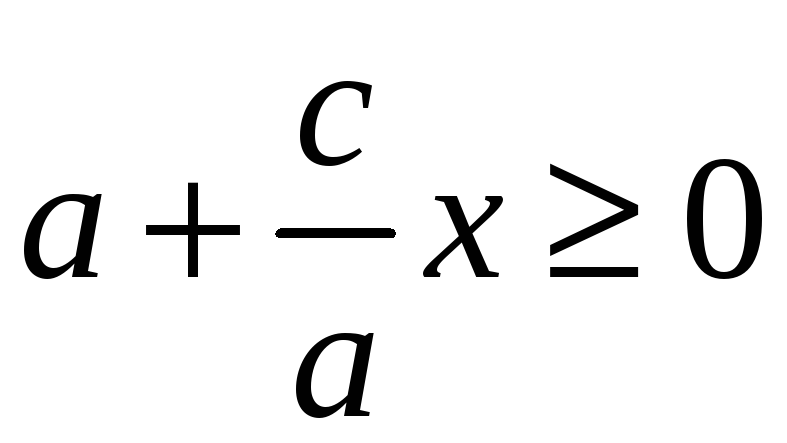. Аналогично получаем расстояние до фокуса . Оно равно . Сумма полученных расстояний равна , т.е. точка принадлежит эллипсу. Таким образом точка принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению . Будем обозначать . Тогда уравнение приобретает вид , причем .