Теорема 23
1) Если поверхность
в пространстве описывается уравнением
,
где
,
то
- плоскость, ортогональная вектору
.
2) Любая плоскость
может быть задана уравнением
,
где
.
Доказательство
1) Так как
,
то будем считать, что
.
Тогда точка
принадлежит поверхности
и уравнение приобретает вид
.
Это выражение является скалярным
произведением вектора
и вектора с координатами
.
Последний является координатами вектора
,
где
- точка с координатами
.
Получили условие на принадлежность
точки
поверхности
:
.
Это условие задает плоскость (см.
определение).
2) Смотри вывод уравнения плоскости.
Способы задания плоскости в пространстве
1) Общее уравнение плоскости
Уравнение плоскости,
ортогональной вектору
,
проходящей через точку
:
или
,
где
2) Пусть заданы
неколлинеарные векторы
и
.
Уравнение плоскости, проходящей через
точку
,
параллельно векторам
и
получаем следующим образом. Вектор
является ортогональным этой плоскости,
поэтому точка
принадлежит плоскости тогда и только
тогда, когда
Если координаты
вектора
,
координаты вектора
,
координаты точки
и координаты точки
,
то условие записывается
3) Если даны три
точки, не лежащие на одной прямой
то
уравнение плоскости, проходящей через
эти точки
4) Параметрическое
задание плоскости. Пусть заданы
неколлинеарные вектора
и
и точка
.
Тогда точка
принадлежит плоскости, проходящей через
точку
параллельно векторам
и
тогда и только тогда, когда вектора
компланарны. Т.к.
и
некомпланарны, то
компланарны тогда и только тогда, когда
найдутся такие
и
такие, что
.
Обозначим координаты векторов:
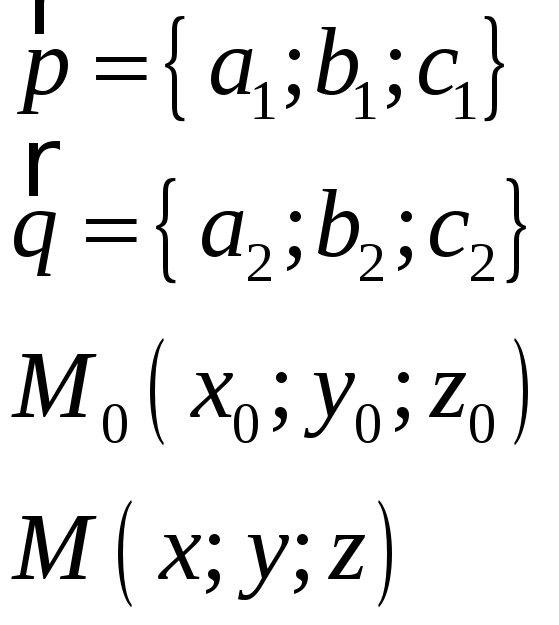
Тогда условие
перепишется
или
5) Нормированное уравнение плоскости
Если в общем
уравнении
(или
)
вектор
обладает свойством
,
то такое уравнение называет нормированным.
Задачи
1) Угол между плоскостями
Определение 52
Углом между плоскостями называется угол, между векторами, ортогональными этим плоскостям.
Замечание
Угол между плоскостями определен неоднозначно. Межу плоскостями может быть два различных угла.
Пусть плоскости заданы уравнениями:
Ортогональные
векторы к этим плоскостям
Угол
между плоскостями определяем из
равенства
2) Расстояние от точки до плоскости
Пусть плоскость
задана уравнением
и точка
принадлежит плоскости. Запишем
нормированное уравнение плоскости:
Обозначим угол
между вектором с координатами
и вектором
через
.
Тогда расстояние от точки
до плоскости равно
,
где
- координаты точки
.
Замечание
Если точка
лежит по ту же сторону от плоскости,
куда направлен вектор
,
то угол
- острый и величина
.
Если точка
лежит по другую сторону от плоскости,
то угол
тупой и величина
.
Прямая в пространстве
Две плоскости в пространстве либо параллельны, либо совпадают, либо пересекаются, и множество точек пересечения плоскостей является прямой. Поэтому прямые в пространстве удобно задавать, как пересечение плоскостей. Тогда уравнение прямой имеет вид
,
где
и НЕ выполняется
Если прямая задана
направляющим вектором
,
т.е. прямая проходящая через точку
содержит точки
такие, что
,
то уравнение прямой можно записать в
каноническом виде:
,
где
Если прямая задана
пересечением плоскостей
,
то для написания канонического уравнения
прямой надо найти направляющий вектор.
,
где
и найти точку, принадлежащую прямой.
Для нахождения общей точки плоскостей
можно воспользоваться методом Крамера.
Пусть дана система
и
.
Тогда
,
где
Доказательство
Домножаем первое
уравнение на
,
а второе на
и вычитаем.
Аналогично
Если уравнение
прямой
,
то не выполняется пропорция
.
Пусть не выполняется первое, т.е.
.
Тогда взяв
подберем
и
системы
Точка с координатами
является точкой прямой.
Задачи
1) Нахождение угла между прямыми
Пусть прямые заданы
уравнениями
