2 Случай

Пусть . Тогда (уравнение второго порядка). Тогда уравнение имеет вид

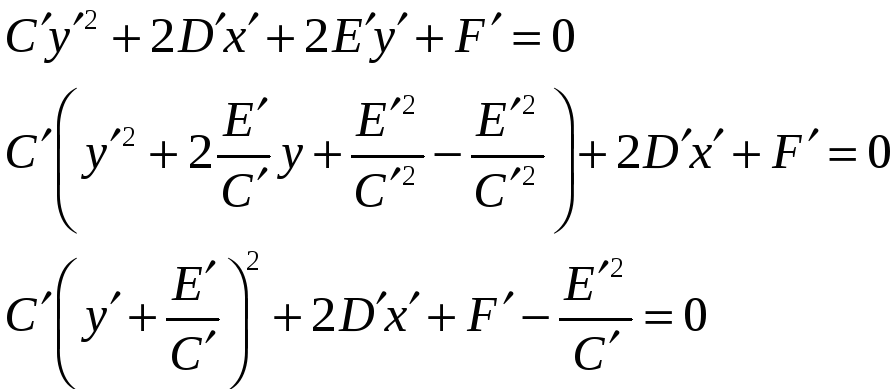С

Если , то

Преобразуем уравнение к виду .

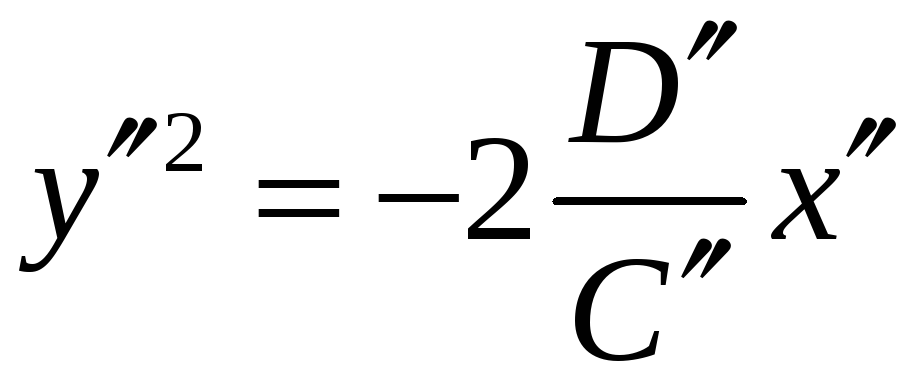Если , то является каноническим уравнением параболы.

Если , то для получения из уравнения канонического уравнения параболы надо перейти к системе координат посредством поворота на угол .

В этой системе координат уравнение имеет вид .

Если , то

Преобразуем это уравнение к виду

. Если , то, обозначив , получаем уравнение . Это уравнение двух параллельных прямых и .

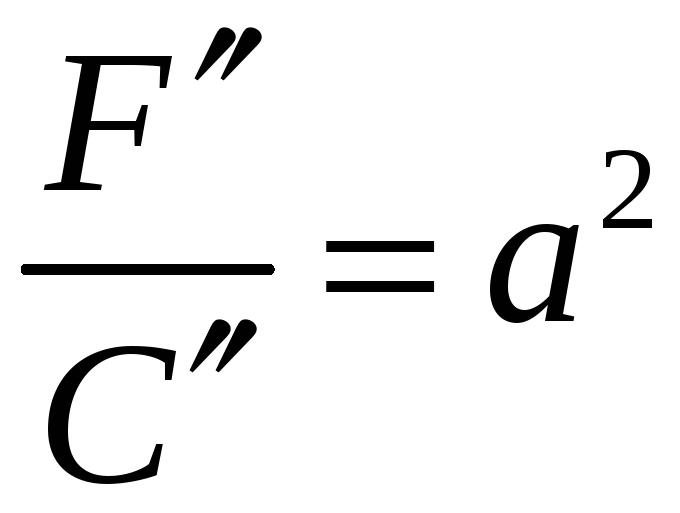Если , то, обозначив , получаем уравнение . Точек на плоскости, удовлетворяющих данному уравнению, нет. Говорят, что это уравнение описывает пару мнимых параллельных прямых.

Если , то уравнение принимает вид . Говорят, что это уравнение описывает пару совпадающих прямых. Таким образом мы доказали теорему.

Теорема 25

Любое уравнение второго порядка путем преобразования системы координат поворотом и переносом начала системы координат можно привести к одному из видов:

1) - эллипс.

2) - вырожденный эллипс.

3) - мнимый эллипс.

4) - гипербола.

5) - пара пересекающихся прямых.

6) - парабола.

7) - пара параллельных прямых.

8) - пара совпадающих прямых.

9) - пара мнимых параллельных прямых.

Теорема 26

Для уравнения второго порядка величины , , являются инвариантными относительно преобразований системы координат посредством поворота и переноса начала системы координат.

1) Если , то уравнение приводится к одному из уравнений или или 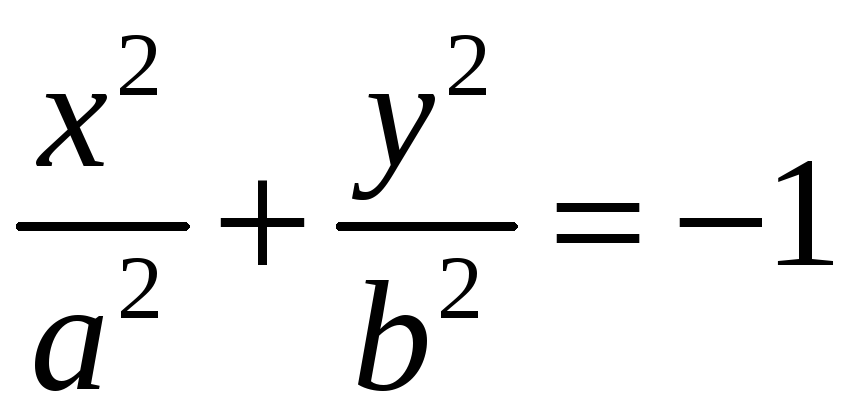При и получаем уравнение эллипса. При и получаем уравнение вырожденного эллипса. При и получаем уравнение мнимого эллипса.

2) Если , то уравнение приводится к одному из уравнений или При получаем уравнение гиперболы. При получаем уравнение пары пересекающихся прямых.

3) Если , то уравнение приводится к одному из уравнений или или или При получаем уравнение параболы. При получаем уравнение пары (параллельных / совпадающих / мнимых параллельных) прямых.

			уравнение
			- эллипс
			- вырожденный эллипс
			- мнимый эллипс
			- гипербола
			- пара пересекающихся прямых
			- парабола
			- пара параллельных прямых или - пара совпадающих прямых или - пара мнимых параллельных прямых

Определение 74

Кривые, для которых называются кривыми эллиптического типа. Кривые, для которых называются кривыми гиперболического типа. Кривые, для которых называются кривыми параболического типа.

Определение 75

Центр симметрии кривой второго порядка называется центром кривой второго порядка.

Определение 76

Если кривая имеет ровно один центр, то такая кривая называется центральной.

Замечание

Центральными кривыми являются эллиптические и гиперболические кривые, т.е. те для которых .

Поверхности второго порядка

Определение 77

Поверхность в пространстве называется поверхностью второго порядка, если в некоторой декартовой системе координат она задается алгебраическим уравнением второго порядка, т.е. уравнением вида

где

Замечание

Было доказано, что если кривая в некотором базисе задается алгебраическим уравнением -ого порядка, то при переходе к другому базису уравнение сохраняло порядок.

Распадающиеся поверхности

Определение 78

Если в некоторой декартовой системе координат уравнение поверхности второго порядка может быть представлено в виде , где , то такая поверхность называется распадающейся поверхностью.

Замечание

Если для распадающейся поверхности в некотором базисе уравнение имеет вид , то и в любом другом базисе она тоже имеет такой вид.

Замечание

Если точка принадлежит распадающейся поверхности, то ее координаты удовлетворяют одному из уравнений , и наоборот – если координаты точки удовлетворяют одному из этих уравнений, то точка принадлежит поверхности.

Уравнения и являются уравнениями плоскостей в пространстве. Если эти уравнен6ия описывают пересекающиеся плоскости, то рассмотрим систему координат, выбранную следующим образом. Ось направлена вдоль прямой пересечения этих плоскостей. В качестве начала координат выберем любую точку на этой прямой. Оси и направим так, чтобы они лежали на биссектрисах двухгранных углов, образованных этими плоскостями. В этом базисе плоскости будут иметь уравнения и и распадающаяся поверхность будет имеет уравнение или .

Если плоскости параллельны и не совпадают, то выберем систему координат так, чтобы плоскость была параллельна указанным плоскостям и находилась посередине между ними. Тогда уравнения плоскостей в этом базисе имеют вид и . Уравнение поверхности второго порядка имеет вид или . Если плоскости совпадают, то выберем систему координат так, чтобы эти плоскости совпадали с плоскостью . Тогда уравнения плоскостей имеют вид и , а уравнение поверхности .