Занятие 1 Прямоугольная система координат

Цели

Знать:

• Основные определения, связанные с методом координат на плоскости;

• основные приложения метода координат на плоскости.

Уметь:

• Составлять уравнение линии в прямоугольной системе координат по заданному её свойству.

▼Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки на плоскости. Одной из таких систем является прямоугольная (декартова) система координат. ▲

▼ Прямоугольная система координат ХОУ задаётся двумя взаимно перпендикулярными прямыми, на каждой из которых выбрано положительное направление и задан единичный отрезок. Эти прямые называются осями координат. Одну из осей называют осью абсцисс и обозначают ОХ, другую — осью ординат и обозначают ОY. ▲

Координаты точки М записывают так: М(х; у); при этом число х называется — абсциссой точки М, а число у — ординатой точки М.

▼ Расстояние между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) на плоскости вычисляется по формуле:

(1). ▲

▼ Координаты (х; у) точки М, делящей в заданном отношении отрезок АВ, где А(х₁; у₁) и В(х₂; у₂), находятся по формулам:

(2). ▲

В частности, при (точка М делит отрезок АВ пополам), получаются формулы координат середины отрезка:

.

▼ Площадь треугольника с вершинами А(х₁; у₁), В(х₂; у₂), С(х₃; у₃) вычисляется по формуле:

(3)

или

, где .▲

№1. Найти точку, симметричную точке А(–2; 4) относительно биссектрисы первого координатного угла.

► Проведём через точку А прямую l₁, перпендикулярную биссектрисе l первого координатного угла. Пусть . На прямой l₁ отложим отрезок СА₁, равный отрезку АС (рис. 1).

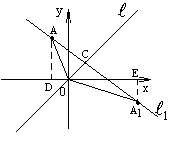
рис.1

Прямоугольные треугольники АСО и А₁СО равны между собой (по двум катетам). Отсюда следует, что |OA|=|OA₁|. Треугольники ADO и OEA₁ также равны между собой (по гипотенузе и острому углу). Заключаем, что |AD|=|OE|=4, |OD|=|EA₁|=2, т.е. точка А₁ имеет координаты х=4, у= –2, т.е. А₁(4; –2).◄

№2. В треугольнике с вершинами А(2; 3), В(6; 3), С(6; –5) найти длину биссектрисы ВМ.

► По свойству биссектрисы внутреннего угла треугольника имеем: .

Найдём, используя формулу (1) длины сторон ВС и ВА треугольника АВС:

, .

Следовательно,

=.

Найдем, используя формулу (2) координаты точки М:

, , т.е. .

Найдём длину биссектрисы ВМ:

,

т.е. . ◄

Задачи для самостоятельного решения

№1. Дана точка А(3; –2). Найти координаты точек, симметричных точке А относительно оси ОX, оси ОY, начала координат.

Ответ: (3; 2); (–3; –2); (–3; 2).

№2. Найти координаты точки, симметричной точке А(2; 4) относительно биссектрисы: 1) второго и четвёртого координатных углов; 2) первого и третьего координатных углов.

Ответ: (4; –2); (4; 2).

№3. Точки А(2; 4), В(–3; 7) и С(–6; 6) — три вершины параллелограмма, причём А и С — противоположные вершины. Найти четвёртую вершину.

Ответ: (–1; 3).

№4. Дан треугольник с вершинами А(–2; 4), В(–6; 8), С(5; –6). Найти площадь этого треугольника.

Ответ: 6 кв.ед.

№5. На оси ординат найти точку, отстоящую от точки А(3; –8) на расстоянии 5 единиц.

Ответ: (0; –4) и (0; –12).

№6. Отрезок с концами А(1; –5) и В(4; 3) разделён на три равные части. Найти координаты точек деления.

Ответ: ; .

№7. Найти координаты точки, одинаково удалённой от осей координат и от координаты точки А(1; 8).

Ответ: (5; 5), (13; 13).

№8. Даны вершины треугольника: А(7; 2), В(1; 9), С(–8; –11). Найти расстояние от точки О пересечения медиан треугольника до вершины В.

Ответ: .

№9. Две противоположные вершины квадрата находятся в точках А(3; 5) и С(1; –3). Найдите его площадь.

Ответ: 34 кв.ед.

№10. Найти площадь четырёхугольника с вершинами А(–3; 2), В(3; 4), С(6; 1), D(5; –2).

Ответ: 20 кв.ед.