Занятие 2 Различные виды уравнения прямой на плоскости Цели

Знать:

• Различные формы записи уравнения прямой на плоскости;

• условия параллельности и перпендикулярности прямых.

Уметь:

• Составлять по заданным условиям уравнение прямой;

• переходить от одного вида уравнения к другому;

• находить связь между коэффициентами общего уравнения прямой и взаимным расположением прямых.

1. Уравнение прямой с угловым коэффициентом

у=kx+b, (4)

где k — угловой коэффициент прямой (т.е. тангенс угла , который прямая образует с положительным направлением оси ОX, ); b — ордината точки пересечения прямой с осью ОY.

2. Общее уравнение прямой

Ах+Ву+С=0, (5)

где А, В и С — постоянные коэффициенты, причём А и В одновременно не обращаются в нуль (т.е. ).

3. Уравнение прямой, проходящей через данную точку М₀(х₀;у₀) в данном направлении

, (6)

где k=tg ( — угол, образуемый этой прямой с осью ОX,); (х₀; у₀) — координаты данной точки.

Уравнение пучка прямых, проходящих через точку пересечения двух прямых и

, (7)

где , принимают всевозможные действительные значения.

4. Уравнение прямой, проходящей через две точки

М₁(х₁;у₁) и М₂(х₂; у₂), где ,

. (8)

Угловой коэффициент этой прямой определяется по формуле:

. (9)

5. Уравнение прямой в отрезках на осях

, (10)

где a, b — длины отрезков (с учётом знаков), отсекаемых прямой на осях Ох и Оу соответственно.

6. Нормальное уравнение прямой

, (11)

где р — длина перпендикуляра, опущенного из начала координат на прямую, — угол, который этот перпендикуляр образует с положительным направлением оси Ох (рис.2).

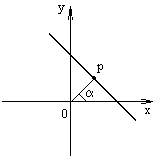
рис.2

Под углом между прямыми в плоскости понимают наименьший (острый) из двух смежных углов, образованными этими прямыми.

Если прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами ; или уравнениями в общем виде ; , то угол между ними вычисляется по формуле:

, (12)

Расстояние d от точки М₀(х₀; у₀) до прямой Ax+By+C=0 вычисляется по формуле:

(13).

№3. Найти уравнение прямой, образующей с ось ОX угол и пересекающей ось ОY в точке (0; 5). Выяснить, проходит ли эта прямая через точки А(2; 3) и В(2; –3). Построить прямую.

► Из условия задачи следует, что отрезок, отсекаемый прямой на оси ординат, b=5, угловой коэффициент k=tg= –1. Следовательно, уравнение прямой с угловым коэффициентом:

у= –х+5.

Подставляя в искомое уравнение прямой координаты точки А вместо текущих координат, получим 3= –2+5, т.е. 3=3. Т.к. координаты точки А удовлетворяют уравнению прямой, то прямая проходит через эту точку.

Подставляя в уравнение координаты точки В, получим . Координаты точки В не удовлетворяют уравнению, следовательно, прямая не проходит через точку В.

Положение прямой определяется двумя точками, принадлежащими ей. Для построения прямой по ее уравнению следует:

1. найти любые две точки, координаты которых удовлетворяют этому уравнению;

2. построить их;

3. через полученные точки провести прямую.

Уравнение данной прямой содержит свободный член, следовательно, эта прямая пересекает оси координат.

Найдём точки пересечения прямой с осями координат и проведём через них прямую. Запишем это в виде таблицы:

х	0	5
у	5	0

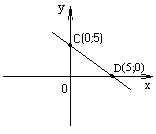
рис.3

Получили точки С(0; 5) и D(5; 0). Построим эти точки и проведём через них искомую прямую (рис.3). ◄

№4. Найти угловой коэффициент прямой и отрезок, отсекаемый ею на оси ординат, зная, что прямая проходит через точки М(2; –1) и Р(–1; 8).

► Воспользуемся уравнением прямой, проходящей через две данные точки (8) подставляя в уравнение вместо х₁, у₁, х₂, у₂ координаты точек М и Р, получаем:

,

отсюда

или у= –3х+5.

Искомое уравнение мы привели к уравнению с угловым коэффициентом, т.е. к уравнению вида у=kx+b. Таким образом, угловой коэффициент искомой прямой k= –3 и начальная ордината b=5.

Угловой коэффициент можно найти также по формуле (9) . ◄

№5. Дан треугольник с вершинами А(4; 6), В( –3; 0), С(2; –3). Найти углы треугольника, уравнения биссектрисы AD, высоты СЕ и точку их пересечения (рис.4).

► Угловые коэффициенты прямых АВ, ВС, АС найдём по формуле (9). Следовательно,

;

;

.

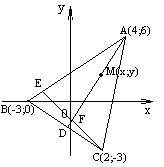
рис.4

Теперь найдём углы треугольника, воспользовавшись формулой (8). Имеем:

, A=arctg 0,75;

, В=arctg 3;

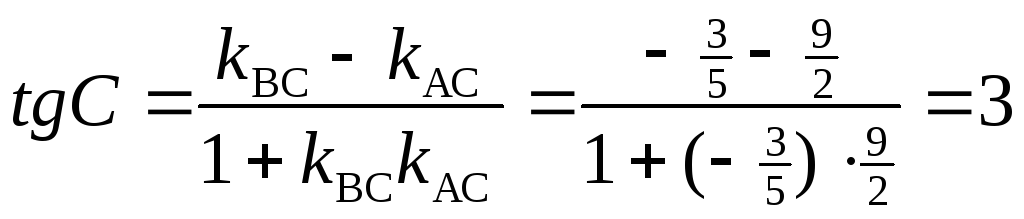, C=arctg 3.

Следовательно — равнобедренный.

Для нахождения уравнения биссектрисы угла А напишем уравнения сторон АВ и АС данного треугольника. Уравнение прямой АВ:

или 6х – 7у+18=0.

Уравнение прямой АС:

или 9х – 2у – 24=0.

Пусть точка М(х; у) лежит на биссектрисе AD (х и у — текущие координаты биссектрисы), тогда она будет одинаково удалена от сторон АВ и АС угла А.

Расстояние d₁ от точки М(х; у) до стороны АВ можно записать так: d₁=, аналогично расстояние d₂= (расстояние от точки М(х; у) до стороны АС.

Так как точки В и С лежат по разные стороны относительно биссектрисы AD, то d₁= – d₂. Следовательно, уравнение биссектрисы AD:

или 5х – 3у – 2=0.

Теперь напишем уравнение прямой СЕ. По условию прямая СЕ перпендикулярна к прямой АВ, следовательно, , т.е. . Учитывая, что прямая СЕ проходит через точку С(2; –3), напишем искомое уравнение:

или 7х+6у+4=0.

Найдём точку пересечения F прямых AD и CE. Для этого решим систему уравнений:

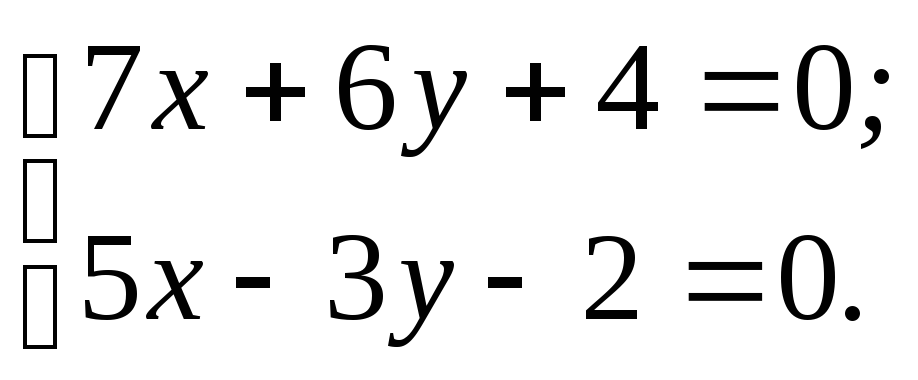
х=0; . Следовательно, искомая точка . ◄