Решение типового варианта индивидуального домашнего задания «Прямая на плоскости»

Задание 1. Даны вершины треугольника АВС: А(4; 3), В( –3; –3), С(2; 7). Найти:

а) уравнение стороны АВ;

б) уравнение высоты СН;

в) уравнение медианы АМ;

г) точку N пересечения медианы АМ и высоты СН;

д) уравнение прямой, проходящей через вершину С параллельно стороне АВ;

е) расстояние от точки С до прямой АВ.

► а) Прямая проходит через две точки А(4; 3) и В( –3; –3), воспользуемся уравнением прямой, проходящей через две точки (8), получим уравнение стороны АВ:

, откуда

6(х – 4)=7(у – 3) или 6х – 7у – 3=0;

б) Угловой коэффициент прямой АВ: k_АВ=. С учётом условия перпендикулярности прямых АВ и СН угловой коэффициент высоты СН: k_СН =.

Составим уравнение высоты СН , проходящей через точку С(2; 7) с угловым коэффициентом , воспользуемся формулой (6):

у – 7=(х – 2) или 7х+6у – 56=0;

в) Найдём координаты точки М — середины отрезка ВС:

; , т.е .

Теперь по двум известным точкам А и М составляем уравнение медианы АМ:

или 2х – 9у+19=0;

г) Для нахождения координат точки N пересечения медианы АМ и высоты СН составляем систему уравнений:

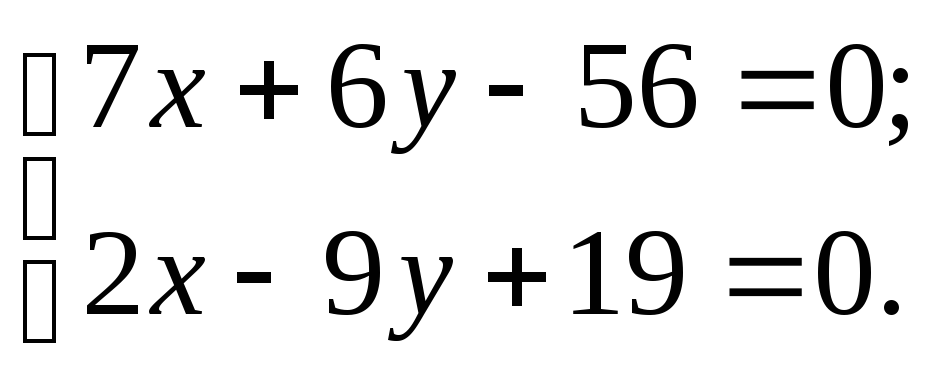
Решая систему, получаем х=, у=, т.е. ;

д) Так как прямая, проходящая через вершину С, параллельна стороне АВ, то их угловые коэффициенты равны k_CD = k_AB = . Тогда используя формулу (6), уравнение прямой СD имеет вид:

у – 7=(х – 2) или 6х – 7у+37=0;

е) расстояние от точки С до прямой АВ вычисляем по формуле (13):

d=|CH|=.

рис.5

Решение задачи проиллюстрировано на рисунке 5. ◄

Задание 2. Известны вершины О(0; 0), А( –2; 0) параллелограмма АОСD и точка пересечения его диагоналей В(2; –2). Записать уравнения сторон параллелограмма.

► Уравнение стороны ОА можно записать сразу: у=0. Так как точка В является серединой диагонали AD, то по формулам деления отрезка пополам можно вычислить координаты вершины D(x; y):

; ,

откуда х=6, у= –4.

Теперь можно найти уравнения всех остальных сторон. Учитывая параллельность сторон ОА и СD, составляем уравнение стороны CD: y= –4.

Уравнение стороны OD составляем по двум известным точкам:

или 2х+3у=0.

Уравнение стороны АС находим, учитывая, что она проходит через известную точку А( –2; 0) параллельно известной прямой OD:

у – 0=(x+2) или 2х+3у+4=0. ◄

Занятие 3 Кривые второго порядка Цели

Знать:

• Определения основных кривых второго порядка и их канонические уравнения;

• определение фокусов, фокусного расстояния, директрис и эксцентриситета линий второго порядка;

Уметь:

• Определять по каноническому уравнению вид кривой второго порядка;

• по заданному каноническому уравнению находить все числовые характеристики линий второго порядка;

• строить кривые второго порядка по каноническому уравнению.

▼ Линии, определяемые алгебраическими уравнениями второй степени

, (14)

называются кривыми второго порядка. ▲

1. Эллипс

▼ Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (рис. 6 а, б).

Каноническое уравнение эллипса:

, (15)

где а=ОА₁=ОА₂ — длина большой полуоси; b=OB₁=ОВ₂ — длина малой полуоси. ▲

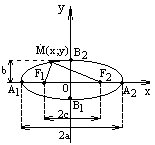
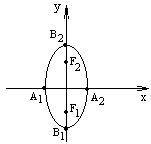
а) б)

рис.6

А₁(–а; 0), А₂(а; 0), В₁(0; –b), B₂(0; b) — вершины эллипса; F₁ и F₂ — фокусы эллипса (левый и правый), расстояние между фокусами F₁F₂=2с — фокусное расстояние.

Зависимость между параметрами a, b и c выражается соотношением:

a² – b²=c².

• если a>b, координаты фокусов F₁(–c; 0), F₂(c; 0), где 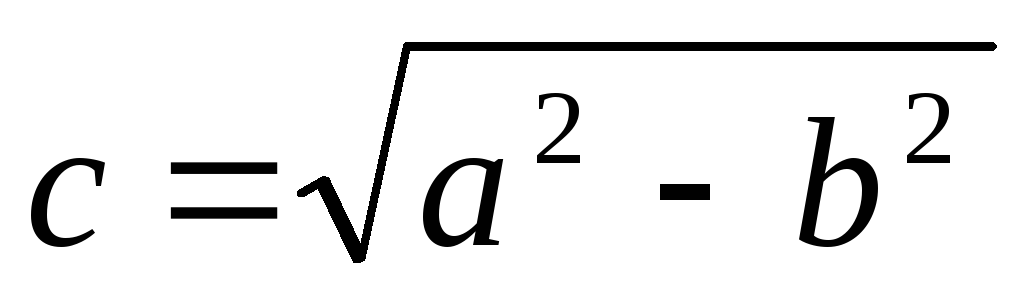(рис.6 а), тогда

эксцентриситет эллипса:

(16.а);

уравнение директрис эллипса:

(17.а).

• если a<b, координаты фокусов F₁(0; –с), F₂(0; с), где 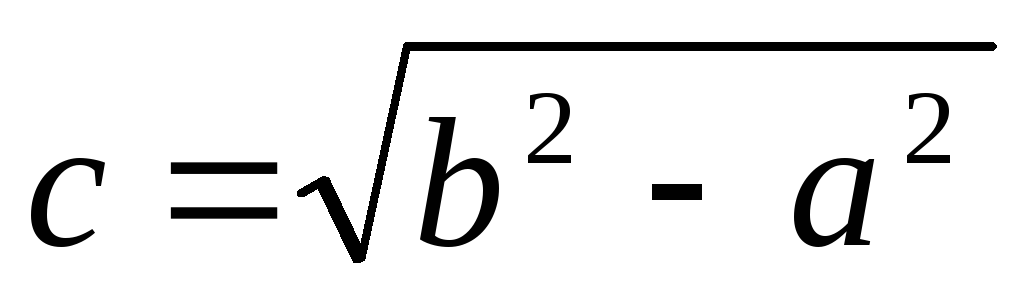(рис.6 б), тогда

эксцентриситет эллипса:

(16.б);

уравнение директрис эллипса:

(17.б).

Фокальные радиусы эллипса:

. (18).