Домашние задания
№112.
В полярной
системе координат построить точки:
А(2; 0);
В
;
С
;
D
;
E
;
F
;
G
;
K
;
L
;
M
.
№113. Написать в полярных координатах уравнения линий:
1)
;
2) у – 2х=0;
3) х2+у2=2а у.
№114.
Построить
линии: 1)
;
2)
;
3)
;
4)
;
5)
.
№115.
Написать в
декартовых координатах уравнения линий
и построить линии: 1)
;
2)
;
3)
.
Дополнительные задания
№116.
Построить
линии, заданные уравнениями в полярных
координатах. Записать в декартовых
координатах: 1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
.
№117. Составить в полярных координатах уравнения следующих линий:
1) прямой, перпендикулярной к полярной оси и отсекающей на ней отрезок, равный 3;
2) прямых, параллельных полярной оси и отстоящих от неё на расстоянии 5;
3) окружности R=4 с центром на полярной оси и проходящей через полюс;
4) окружностей радиусом R=3, касающихся полярной оси в полюсе.
Ответ:
1)
;
2)
;
3)
;
4)
.
Решение типового варианта индивидуального домашнего задания «Кривые второго порядка»
Задание 1. Составить канонические уравнения:
а)
эллипса, большая полуось которого равна
3, а фокус находится в точке
;
б)
гиперболы с мнимой полуосью, равной 2,
и фокусом
;
в) параболы, имеющей директрису х= –3.
►а)
Каноническое уравнение эллипса имеет
вид
.
По условию большая полуось, а=3,
с=
.
Для эллипса: c2=a2 – b2,
следовательно, b2=32 – 
=4.
Искомое уравнение:
;
б)
Каноническое уравнение гиперболы имеет
вид
.
По условию мнимая полуось b=2,
c=
.
Для гиперболы: c2=a2+b2,
следовательно, а2=с2 – b2=
– 22=9.
Искомое уравнение гиперболы:
.
в)
Каноническое уравнение параболы в
данном случае имеет вид у2=2 р х,
уравнение её директрисы
,
но по условию задачи уравнение директрисы
х= – 3,
поэтому
;
р=6.
Искомое каноническое уравнение параболы
имеет вид: у2=12х. ◄
Задание 2. Записать уравнение окружности, проходящей через фокусы эллипса х2+4у2=4 и имеющей центр в его верхней вершине.
► Для
данного эллипса
верхняя вершина А(0; 1),
а=2,
b=1.
Поэтому с=
=
=
.
Таким образом, фокусы находятся в точках
F1(–
;0),
F2(
;0).
Радиус искомой окружности вычисляем по формуле расстояния между двумя точками:
R=|AF1|=|AF2|=
=
=2.
В соответствии с уравнением (15) записываем искомое уравнение окружности:
(х – 0)2+(у – 1)2=22 или х2+(у – 1)2=4.◄
Задание 3. Составить уравнение линии, каждая точка М которой отстоит от точки А(3; 2) на расстоянии, в три раза большем, чем от точки В(–1; 0).
► Пусть М(х; у) — любая точка искомой линии (рис.19).
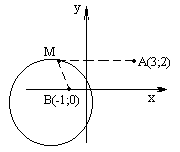
рис.19
Тогда
по условию задачи |AM|=3|BM|.
Т.к. |AM|=
,
|BM|=
,
то уравнение искомой линии:
=3
.
Преобразуем его, возведя обе части в квадрат. Имеем:
х2 – 6х+9+у2 – 4у+4=9х2+18х+9+9у2,
8х2+24х+8у2+4у – 4=0.
Выделив полные квадраты в последнем уравнении, придём к уравнению вида:
,
которое
является уравнением окружности с центром
в точке
и радиусом R=
.
◄
Задание 4. Построить кривую, заданную
уравнением в полярных координатах
.
► Составим
таблицу, в которой приведены значения
полярного угла
и соответствующие им значения полярного
радиуса
:
|
|
|
|
|
|
|
|
|
|
0 |
4 |
|
0 |
|
4 |
|
8 |
|
|
2 |
|
0,6 |
|
6 |
|
7,4 |
|
|
1,2 |
|
1,2 |
|
6,8 |
|
6,8 |
|
|
0,6 |
|
2 |
|
7,4 |
|
6 |
Построив найденные точки в полярной системе координат и соединив их плавной линией, получим кардиоиду. ◄