2. Построение q

Вспомним, как мы строили Z из N. Мы сначала «удвоили» N, то есть рассмотрели множество пар натуральных чисел – элементов NN=N². Затем, исходя из того, что в уравнении a+x=b пара (a,b) (a,b) определяет х с точностью до слагаемого, прибавляемого к обеим частям уравнения, ввели на множестве N² бинарное отношение эквивалентности R: (a,b)(c,d) тогда и только тогда, когда a+d =b+c. В краткой записи: (a,b) R (c,d)a+d =b+c. Не похоже на то, что было там? Там было то, что точки (a,b) и (c,d) лежали на одном луче, параллельном лучу (i,i), iN. Это имеет место тогда, когда при некотором натуральном числе n либо a+n=c, b+n=d, либо c+n=a, d+n=b. Проверьте, что в обоих случаях выполняется a+d =b+c. Проверьте также, что и обратно, если выполняется a+d =b+c, то nN׀((a+n=c)(b+n=d))(c+n=a)(d+n=b)).

Упражнение 3.

Проверьте, что отношение R действительно является отношением эквивалентности.

Теперь таким же образом приступим к построению Q из Z. Расширяя N, мы добивались (и добились!) того, чтобы уравнение a+X=b было всегда разрешимо (в N оно разрешимо только при a<b). Иными словами, в построенном нами Z выполнима операция вычитания. Теперь займёмся уравнением aX=b, (a,bZ). Если а=0, то оно либо не имеет решений (при b0), либо имеет бесконечно много решений (при b=0). В любом случае, при а=0 оно не определяет никакого конкретного числа X. Поэтому считаем, что а0 (b может равняться 0  в этом случае X=0).

Р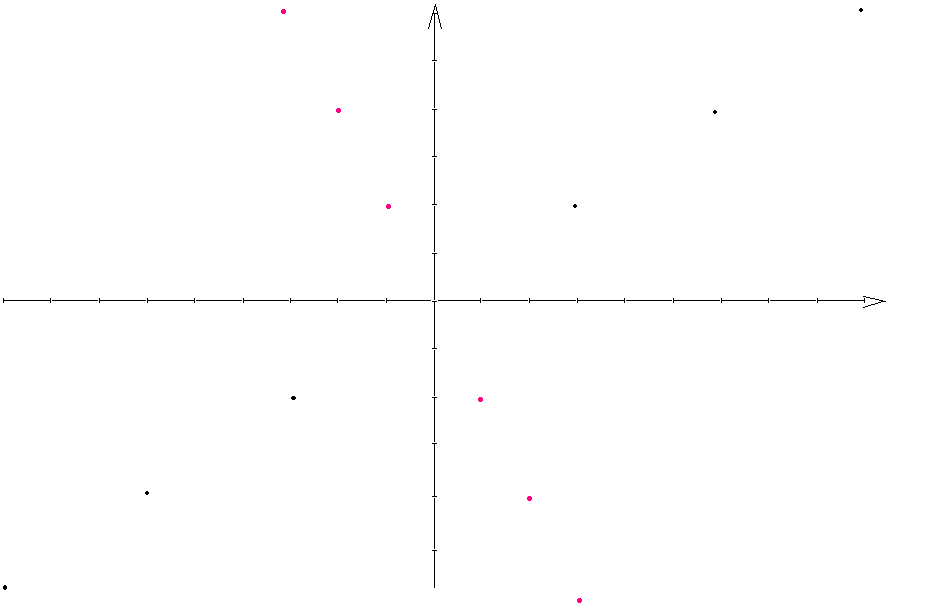 ешение уравнения aX=b (по причине, которая выяснится позже, называемое также корнем) зависит от чисел a и b. Отметим пару (a,b) на целочисленной плоскости. Число b называется числителем корня X, а число а – его знаменателем. Для наглядности возьмём, к примеру, 2х=3 и соответствующую ей пару (2,3). Эта пара – элемент ZZ. Поскольку обе части уравнения можно умножать на одно и то же число, число Х будет служить корнем для всех уравнений сaХ =сb, сZ. Единственно, кого нужно исключить из числа множителей, это число 0. При умножении на него, равенство, конечно, останется верным (0=0), но ему, помимо Х, удовлетворят все числа. Оно уже не определяет однозначно никакого числа. Поэтому точку (0,0) из множества точек (сb,сa) придётся исключить. Итак, рациональное число х=[a,b]={(ca,cb), cZ, c0}. Посмотрите, как выглядит это множество точек для разных пар (a,b). Если в случае с (NN) мы имели дело с пучком параллельных лучей, то теперь мы имеем дело с пучком целочисленных прямых. Они не пересекаются, ибо точка (0,0), в которой они все должны были бы пересекаться, им не принадлежит.

Упражнение 4.

Докажите, что определённое так бинарное отношение R (две точки эквивалентны, если они лежат на одной прямой, проходящей через точку (0,0), но ни одна из них не является этой точкой) является отношением эквивалентности. Проверьте, что это же отношение можно задать условием (a,b)R(c,d)  ad=bc. Определим теперь сложение и умножение этих объектов – построенных прямых (они и будут элементами Q – множеством рациональных чисел).

Для этого посмотрим, как обстоит дело в случаях, когда уравнение ax=b разрешимо в Z. Например, возьмём 2х=4 и 3у=9. Если мы эти равенства перемножим – их левые части и их правые части, то получим: 2х3у=49, то получим: (23) (ху)=49. Получилось, что произведение корней удовлетворяет уравнению, полученному из произведений левых частей и правых частей. Распространим это правило и на те случаи, когда уравнение ax=b неразрешимо в Z: пусть числа-прямые [a,b] и [c,d] определяются их представителями (a,b) и (c,d). Тогда их произведением назовём прямую [ac, bd].

Упражнение 5.

Докажите корректность этого определения.

То есть, умножать рациональные числа просто: числитель произведения равен произведению числителей сомножителей, а знаменатель – произведению их знаменателей.

Теперь перейдём к сложению.

Cначала рассмотрим числа X,Y с одинаковым знаменателем: X=[a,b] Y=[a,c]). Иными словами, aX=b; aY=c. Сложим эти уравнения: aX+aY=b+c.

Ввиду дистрибутивности, доказанной для Z, можно вынести в левой части общий множитель а: а(X+Y)=b+c. Получилось, что X+Y=[ а, b+c]. То есть, сложение рациональных чисел с одинаковым знаменателем просто: складываем числители, а знаменатель (общий) не меняем. Геометрически это означает, что если у двух прямых есть точки с одинаковыми абсциссами, то мы просто на прямой, соединяющей эти точки (она проходит параллельно оси ординат) складываем их ординаты, и через полученную точку проводим (однозначно определённую!) прямую. А что делать в общем случае, когда знаменатели разные? Докажем, что у любой пары прямых найдутся точки, лежащие на прямой, параллельной оси ординат.

Пусть Х=[a,b] У=[c,d]. Поскольку, умножая числитель и знаменатель рациональных чисел Х иУ на одно и то же целое число, мы лишь двигаемся вдоль этих прямых, то имеют место Х=[ac, bс] У=[сa, dа]. Вот мы и получили точки (на тех же прямых!), лежащие на одной вертикали. Заодно и получили правило сложения двух рациональных чисел (приведение к общему знаменателю).

Упражнение 6.

1. каким прямым (элементам Q) соответствуют целые числа (элементы Z)?

2. Какая прямая соответствует нулю?

3. Чем отличаются прямые, соответствующие натуральным (положительным целым) числам от прямых, соответствующих целым отрицательным числам?

4. Докажите, что Q замкнуто относительно операций сложения и умножения, то есть эти операции всегда выполнимы в Q (в результате их выполнения вновь получается число из Q)..

5. Докажите, что в Q всегда выполнима операция вычитания, т.е, разрешимо уравнение [b,a]+[x,y]=[c,d].

6. Докажите, что в Q всегда, кроме деления на 0, выполнима операция деления т.е, разрешимо уравнение [b,a][x,y]=[c,d] если [b,a]0.

7. Какой элемент служит нейтральным относительно операции умножения, то есть такой еQ, что еq=q qQ?

8. Какой элемент служит обратным элементу q=[b,a] (относительно операции умножения), то есть такой рQ, что рq=е.

9. Проверьте выполнение законов коммутативности, ассоциативности и дистрибутивности в Q.

Введём теперь отношение порядка в Q.

Назовём числа, числитель и знаменатель которых одного знака положительными (т.е. >0), а те, у которых они разных знаков – отрицательными (т.е. <0).

Положим a>b, если a-b>0.

Упражнение 7.

а) Докажите, что это определение корректно.

b) Докажите, что отношение порядка в Q согласовано c арифметическими операциями: p>q aQ p+a>q+a ; aZa>0, pa>qa; -q>-p

c) Докажите, что теперь, в отличие от N и Z, ни у какого элемента нет ни непосредственно предшествующего, ни непосредственно следующего: между любыми двумя элементами p > q найдётся третий элемент r, такой, что p>r>q.

Как этот факт истолковать геометрически?

Каких же представителей нам удобно выбрать в случае рациональных чисел-прямых?

В случае, когда они проходят через первый и третий квадранты плоскости, в первом квадранте выберем ту точку, которая ближе всего к началу координат. У неё числитель и знаменатель – взаимно простые натуральные числа (не имеют общих делителей, кроме 1). Это так называемая несократимая дробь. В случае, когда прямая проходит через второй и четвёртый квадранты, выбираем ту из двух симметричных точек, ближайших к началу координат, которая находится во втором квадранте. У них также НОД числителя и знаменателя равен 1.

Если мы упорядочим наши прямые по величине, то на плоскости установится общепринятая ориентация: числа будут расти при повороте против часовой стрелки. Поскольку внутри любого, сколь угодно острого угла найдутся целочисленные точки, то между любыми двумя целочисленными конкурентными прямыми проходит третья.

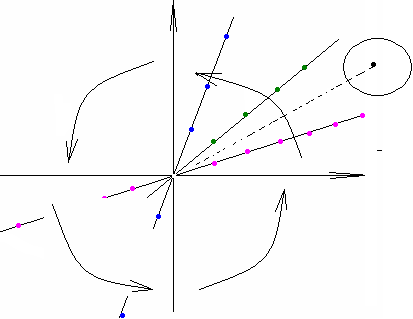Перенесём наши построения на прежнюю числовую прямую, на которой до этого были лишь целочисленные точки ….-2, -1, 0, 1, 2,… . Для этого перенумеруем наши прямые (а то, что это можно сделать – повесить натуральный номерок на каждую из построенных прямых и никого не упустить, мы докажем позже) и начнём по очереди ставить каждой прямой в соответствие точку на числовой прямой так, чтобы сохранялся порядок точек: если прямая а была меньше прямой b, то соответствующая ей точка А на прямой лежит левее точки В. Сначала легко находим два последовательных целых числа (две рядом расположенные целочисленные точки на прямой), между которыми должна находиться наша новая точка- образ прямой, а затем сравниваем с конечным (всегда лишь конечное число точек предшествует новой точке) числом точек-образов на этом интервале уже находящимся. Теперь на нашей числовой прямой больше стало точек, заполнилось много «дыр» между соседними целыми числами. В любом, сколь угодно малом, отрезке числовой прямой теперь окажутся рациональные точки. Этот факт выражают термином «рациональные числа всюду плотны на числовой прямой». Более того, если бы мы даже ограничились только числами со знаменателями-степенями 10 (десятичные числа) или любого другого числа (например, двойки – половинки, четвертинки, осьмушки и т.д.) то и тогда они бы заполнили плотно всю прямую. Однако дыры на ней всё-таки остались. Более того, их в каком-то смысле даже больше, чем рациональных чисел (дробей). Прямая по-прежнему дырява, как решето. Заполнить её окончательно предстоит нам в следующем классе.

III. Отрицательные степени.

Теперь, когда мы у нас появились отрицательные числа и дроби, появилась и возможность расширить наше понятие о степени. До этого у нас уже встречались степени натуральных чисел с натуральным показателем. Например, рассмотрим степени двойки:

22=2²;

222=2³;

222´2=2⁴;

2´222´2=2⁵

При переходе к каждой следующей строчке происходит умножение числа на два и увеличение степени на единицу. Теперь обратим нашу таблицу и начнём спускаться по ступенькам-степеням вниз:

2´222´2=2⁵;

222´2=2⁴;

222=2³;

22=2²;

Упражнение 8.

Продолжите таблицу дальше: 2¹=__; 2⁰=__; 2^-1=___; 2^-2=___; 2^-3=___;

Упражнение 9.

Докажите, что для натуральных чисел i,j,k верно правило умножения степеней: kⁱk^j=k^i+j. Здесь уместно вспомнить про индукцию по двум переменным.

Докажите, затем, что оно по-прежнему имеет место и для любых целых чисел i,j.

Докажите, что оно остаётся верным, если i,jZ, а kQ

Упражнение 10.

Докажите ещё одно правило работы со степенями: . Здесь AQ, а B,CZ.

Упражнение 11.

Вывести для шестеричной системы счисления признаки делимости на 2,3,5 и 7.

Ну, а как с дробями? Ведь имеем же мы дело, например, с десятичными дробями. А как будет с двоичными дробями, троичными, восьмеричными?

А так же. Если 235,45=2×10²+3×10+5+4×10^-1+5×10^-2,

то 653,24₇=6×7²+5×7+3+2×7^-1+4×7^-2. Сложение, умножение и деление таких дробей производится точно так же, как и десятичных. Перевод же из одной системы в другую прост лишь в том случае, если основание одной системы счисления кратно другому. Проверьте сначала это на примерах, а потом попробуйте сформулировать причину, почему это так.

*Упражнение 12.

1. Запишите 2,12₃ в девятеричной системе; в шестеричной системе.

2. Запишите 31,23₄ в двоичной системе; в восьмеричной системе.

3. Выполните деление в шестеричной системе (без остатка) 4501₆:13₆

4. Выполните деление в девятеричной системе (без остатка) 15001₉:3₉

5. Запишите в троичной системе число

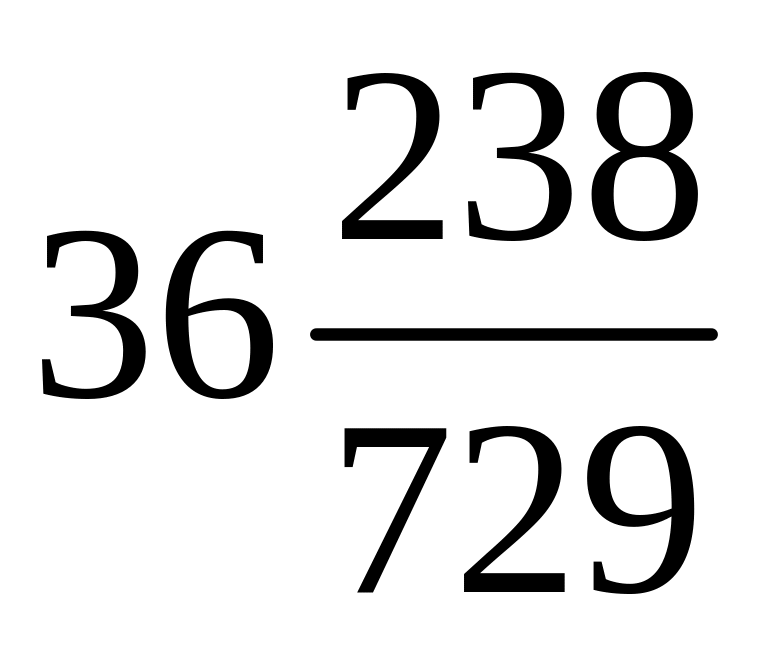
6. Выдвиньте гипотезу, и попытайтесь её обосновать: в каких случаях в результате деления получится конечная дробь, а в каких возникнет бесконечная (периодическая) дробь (вроде, 3,333…, получающаяся при делении 10 на 3).

Упражнение 13.

Проверьте, что и примените это к вычислению суммы .