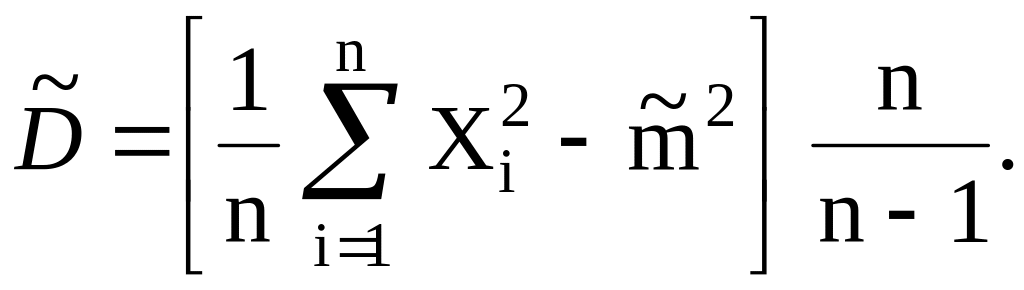- •Конспект лекций По дисциплине «Моделирование систем» Содержание
- •1.Системы и моделирование
- •1.1.Система как предмет моделирования
- •1.2.Модели
- •1.3.Математическое моделирование
- •2.Математические схемы моделирования систем
- •2.1.Основные подходы к построению математических моделей систем
- •2.2.Задачи теории массового обслуживания
- •2.3.Поток заявок. Время обслуживания
- •2.4.Простейшие смо и их характеристики
- •3.Этапы машинного моделирования систем
- •3.1.Построение концептуальной модели системы и ее формализация
- •3.2.Алгоритмизация модели системы и ее машинная реализация
- •3.3.Получение и интерпретация результатов моделирования системы
- •4.Принципы имитационного моделирования сложных систем
- •4.1.Понятие модельного времени
- •4.2.Способы имитации
- •4.3.Моделирующий алгоритм
- •5.Моделирование случайных факторов
- •5.1.Принципы моделирования случайных элементов
- •5.2.Требования к генератору случайных чисел
- •5.3.Методы построения программных датчиков бсв
- •5.4.Моделирование случайных воздействий на системы
- •6.Программные средства моделирования систем
- •6.1.Машинная реализация имитационных моделей
- •6.2.Классификация языков моделирования
- •6.3.Средства языков моделирования
- •7.Язык и система моделирования gpss
- •7.1.Транзакты
- •7.2.Списки
- •Процедура просмотра списка текущих событий:
- •7.3.Устройства
- •7.4.Многокнальные устройства (мку)
- •7.5.Логические ключи
- •7.6.Очереди и регистраторы очередей
- •7.7.Таблицы
- •7.8.Ячейки (Сохраняемые величины)
- •7.9.Матрицы
- •7.10.Функции
- •7.11.Переменные
- •8.Обработка результатов имитационного моделирования
- •8.1.Точечные оценки неизвестных параметров
- •8.2.Статистические методы обработки
- •8.3.Задачи обработки результатов моделирования
- •9.Планирование имитационных экспериментов
- •9.1.Общие принципы и задачи планирования экспериментов
- •9.2.Планирование экспериментов по исследованию систем методами дисперсионного анализа
- •10 Тактическое планирование машинных экспериментов с моделями систем
- •10.1 Стратегии запуска
- •10.1.1 Задание начальных условий
- •10.1.2 Процедуры отсечения
- •10.2 Определение объема имитационных экспериментов
- •9.3.Методы понижения дисперсии
- •Дополняющая выборка
- •Общие потоки случайных чисел
- •Использование априорной информации
- •Использование управляющих переменных
- •9.4.Правила остановки
- •10.Планирование экспериментов по оптимизации систем
- •10.1.Общие положения
- •10.2.Метод крутого восхождения
8.1.Точечные оценки неизвестных параметров
На практике нередко приходится иметь дело со статистическим материалом весьма ограниченного объема — с двумя-тремя десятками наблюдений, часто даже меньше. Это обычно связано с дороговизной и сложностью каждого отдельного опыта. Такого ограниченного материала явно недостаточно для того, чтобы найти заранее неизвестный закон распределения случайной величины (СВ), но все же он может быть использован для получения некоторых сведений о ней. Одной из форм описания неизвестных параметров СВ являются их точечные оценки.
Предположим, что мы хотим определить
по результатам n опытов
некоторый параметр a,
связанный с законом распределения СВ
X. Будем называть
приближенное значение параметра a
его оценкой. Обозначим
![]() оценку параметра a:
оценку параметра a:
![]()
Итак, любая оценка
параметра a — случайная
величина — функция n
случайных величин
![]() (n “экземпляров”
СВ X). Закон распределения
этой случайной величины
зависит от закона распределения случайной
величины X и от вида
функции
(n “экземпляров”
СВ X). Закон распределения
этой случайной величины
зависит от закона распределения случайной
величины X и от вида
функции
![]() ,
выражающей
через
,
а значит и от числа опытов n.
Предъявим к оценке
ряд требований, которым она должна
удовлетворять, чтобы быть в каком-то
смысле “доброкачественной” оценкой.
,
выражающей
через
,
а значит и от числа опытов n.
Предъявим к оценке
ряд требований, которым она должна
удовлетворять, чтобы быть в каком-то
смысле “доброкачественной” оценкой.
Естественно потребовать от оценки
,
чтобы при увеличении числа опытов n
она приближалась (сходилась по вероятности)
к искомому параметру a
![]() .
Оценка, обладающая таким свойством,
называется состоятельной.
.
Оценка, обладающая таким свойством,
называется состоятельной.
Кроме того, желательно, чтобы, пользуясь величиной вместо a, мы, по крайней мере, не делали систематической ошибки в сторону завышения или занижения, т.е. чтобы выполнялось условие:
![]()
Оценка, обладающая таким свойством, называется несмещенной.
Наконец, желательно, чтобы выбранная несмещенная оценка была как можно менее случайной, т.е. обладала по сравнению с другими минимальной дисперсией:
![]()
Оценка, обладающая таким свойством, называется эффективной.
Ограничимся нахождением — по результатам
опытов оценок для математического
ожидания m и дисперсии
D случайной величины
X:
![]()
Естественной оценкой для математического ожидания m СВ X является среднее арифметическое ее наблюденных значений (или статистическое среднее):
![]()
Нетрудно убедиться, что эта оценка состоятельна. Найдем ее математическое ожидание:
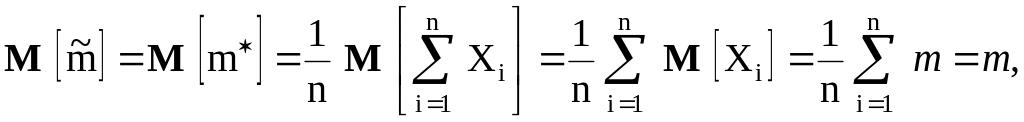
то есть оценка
![]() для m является
несмещенной. В частности доказано что
если СВ X распределена
нормально, то оценка
для m является
несмещенной. В частности доказано что
если СВ X распределена
нормально, то оценка
![]() для математического ожидания m
является и эффективной.
для математического ожидания m
является и эффективной.
Перейдем к оценке для дисперсии D. Оценка (принимаем без доказательства)
![]()
состоятельна, однако, не является
несмещенной. Пользуясь оценкой
![]() вместо D, мы будем
совершать некоторую систематическую
ошибку в меньшую сторону. Чтобы ее
ликвидировать достаточно, выполнить
следующее
вместо D, мы будем
совершать некоторую систематическую
ошибку в меньшую сторону. Чтобы ее
ликвидировать достаточно, выполнить
следующее
![]() ,
,
тогда мы получим несмещенную
оценку для дисперсии, равную статистической
дисперсии, умноженной на n
и деленной на
![]() .
.
При больших значениях n
поправочный множитель
![]() становится близким к единице, и его
применение теряет смысл.
становится близким к единице, и его
применение теряет смысл.
Сформулируем правило приближенного нахождения математического ожидания m и дисперсии D случайной величины X по опытным данным. В качестве приближенных значений (оценок) этих характеристик нужно взять:
![]() (8.1)
(8.1)
или