
- •Конспект лекций По дисциплине «Моделирование систем» Содержание
- •1.Системы и моделирование
- •1.1.Система как предмет моделирования
- •1.2.Модели
- •1.3.Математическое моделирование
- •2.Математические схемы моделирования систем
- •2.1.Основные подходы к построению математических моделей систем
- •2.2.Задачи теории массового обслуживания
- •2.3.Поток заявок. Время обслуживания
- •2.4.Простейшие смо и их характеристики
- •3.Этапы машинного моделирования систем
- •3.1.Построение концептуальной модели системы и ее формализация
- •3.2.Алгоритмизация модели системы и ее машинная реализация
- •3.3.Получение и интерпретация результатов моделирования системы
- •4.Принципы имитационного моделирования сложных систем
- •4.1.Понятие модельного времени
- •4.2.Способы имитации
- •4.3.Моделирующий алгоритм
- •5.Моделирование случайных факторов
- •5.1.Принципы моделирования случайных элементов
- •5.2.Требования к генератору случайных чисел
- •5.3.Методы построения программных датчиков бсв
- •5.4.Моделирование случайных воздействий на системы
- •6.Программные средства моделирования систем
- •6.1.Машинная реализация имитационных моделей
- •6.2.Классификация языков моделирования
- •6.3.Средства языков моделирования
- •7.Язык и система моделирования gpss
- •7.1.Транзакты
- •7.2.Списки
- •Процедура просмотра списка текущих событий:
- •7.3.Устройства
- •7.4.Многокнальные устройства (мку)
- •7.5.Логические ключи
- •7.6.Очереди и регистраторы очередей
- •7.7.Таблицы
- •7.8.Ячейки (Сохраняемые величины)
- •7.9.Матрицы
- •7.10.Функции
- •7.11.Переменные
- •8.Обработка результатов имитационного моделирования
- •8.1.Точечные оценки неизвестных параметров
- •8.2.Статистические методы обработки
- •8.3.Задачи обработки результатов моделирования
- •9.Планирование имитационных экспериментов
- •9.1.Общие принципы и задачи планирования экспериментов
- •9.2.Планирование экспериментов по исследованию систем методами дисперсионного анализа
- •10 Тактическое планирование машинных экспериментов с моделями систем
- •10.1 Стратегии запуска
- •10.1.1 Задание начальных условий
- •10.1.2 Процедуры отсечения
- •10.2 Определение объема имитационных экспериментов
- •9.3.Методы понижения дисперсии
- •Дополняющая выборка
- •Общие потоки случайных чисел
- •Использование априорной информации
- •Использование управляющих переменных
- •9.4.Правила остановки
- •10.Планирование экспериментов по оптимизации систем
- •10.1.Общие положения
- •10.2.Метод крутого восхождения
2.3.Поток заявок. Время обслуживания
Рассмотрим СМО, на которую поступает поток заявок. Так как моменты поступления заявок заранее неизвестны (случайны), то поток заявок можно рассматривать как случайный поток событий.
Важнейшей характеристикой потока заявок является его плотность, или интенсивность — среднее число заявок, поступающих в единицу времени. Если интенсивность потока постоянна, он называется стационарным, если она меняется в зависимости от времени, поток называется нестационарным.
Если заявки поступают в случайные моменты, независимо друг от друга, то они образуют пуассоновский поток. Характерными чертами пуассоновского потока заявок являются ординарность и отсутствие последействия (т. е. заявки поступают поодиночке и независимо друг от друга).
Для приближенного решения задач массового обслуживания обычно заменяют случайный, но не пуассоновский поток заявок пуассоновским. Расчеты показывают, что такая замена, как правило, мало сказывается на пропускной способности системы.
Наиболее простым пуассоновским потоком является такой, у которого интенсивность не зависит от времени:
![]() .
.
Такой поток называется простейшим. Наиболее важные результаты в ТМО получены для простейшего потока заявок.
Кроме характера потока заявок работа
СМО существенно зависит от ее собственных
характеристик: числа каналов n
и работоспособности каждого канала.
Работоспособность канала характеризуется
временем обслуживания одной
заявки. Это время
есть вообще случайная величина и от
заявки к заявке меняется. Поэтому, чтобы
охарактеризовать работоспособность
канала, нужно задать закон распределения
![]() времени обслуживания.
времени обслуживания.
Математические задачи ТМО решаются особенно просто, если предположить, что время обслуживания распределено по показательному закону:
![]()
где
![]() — величина, обратная среднему времени
обслуживания одной заявки
— величина, обратная среднему времени
обслуживания одной заявки
![]() .
.
При пуассоновском потоке заявок и показательном времени обслуживания процесс функционирования СМО будет так называемым марковским случайным процессом, т. е. таким процессом, в котором вероятность любого будущего состояния системы зависит только от ее состояния в данный момент и не зависит от того, каким образом и когда система пришла в это состояние.
2.4.Простейшие смо и их характеристики
Остановимся на моделях СМО, описываемых в классе марковских процессов типа “гибель и размножение” как наиболее распространенных на практике при выполнении инженерных расчетов показателей эффективности: источник содержит только однородные требования, поток требования является простейшим (стационарным пуассоновским потоком), закон обслуживания является показательным, дисциплина обслуживания FIFO.
Многоканальные и одноканальные системы
без потерь с неограниченным ожиданием
и источником с бесконечным числом
требований. В этом случае предполагается,
что система содержит n
обслуживающих одинаковых приборов с
одинаковой интенсивностью обслуживания
при входном потоке
с интенсивностью .
Сообщим без доказательства естественное
условие существования конечной
средней очереди для многоканальных
систем:
![]() или
или
![]() ,
где
,
где
![]() ,
а для одноканальных — при условии
,
а для одноканальных — при условии
![]() или
или
![]() ,
где
,
где
![]() .
.
Многоканальные системы |
Одноканальные системы |
Вероятность простоя |
|
|
|
Среднее число требований в очереди |
|
|
|
Среднее время ожидания требования в очереди |
|
|
|
Среднее число занятых каналов |
|
|
|
Среднее число требований в системе |
|
|
|
Среднее время пребывания требования в системе |
|
|
|
Многоканальные и одноканальные системы с потерями и источником бесконечного числа требований. Предполагаем, что потери возникают по причине ограниченности очереди (накопителя). Очередь ограничена по длине величиной m, т. е. имеются m мест для ожидания требований. В случае если все приборы заняты, и накопитель полностью заполнен, требование теряется.
Многоканальные системы |
Среднее число требований в очереди |
|
Среднее время ожидания требования в очереди |
|
Среднее число требований в системе |
|
Среднее время пребывания требования в системе |
|
Все интересующие показатели для
одноканальных СМО могут быть получены
из соответствующих формул при
![]() .
.
Многоканальные и одноканальные системы без потерь с источником конечного числа требований. В данном случае рассматриваются СМО, в которых интенсивность потока поступающих требований зависит от состояния системы. В такой системе содержится всегда конечное число требований m.
Многоканальные системы |
Одноканальные системы |
Вероятность простоя |
|
|
|
Среднее число требований в очереди |
|
|
|
Среднее время ожидания в очереди |
|
|
|
Среднее число требований в системе |
|
|
|
Среднее время пребывания требования в системе |
|
|
|
Заметим, что в этих и предыдущих СМО финальные вероятности будут существовать при любых значениях и , так как число состояний системы конечно.
Задачи ТМО имеют простое аналитическое решение только в случае, когда поток заявок является пуассоновским. Если это не так, математический аппарат становится очень сложным и приходится, как правило, прибегать к имитационному моделированию работы системы.

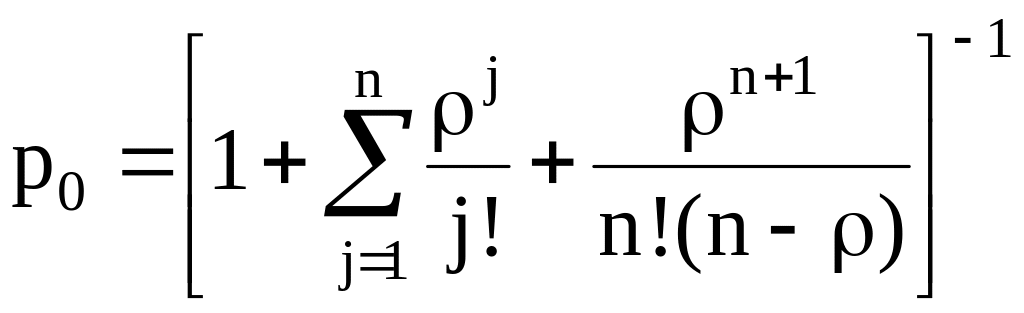
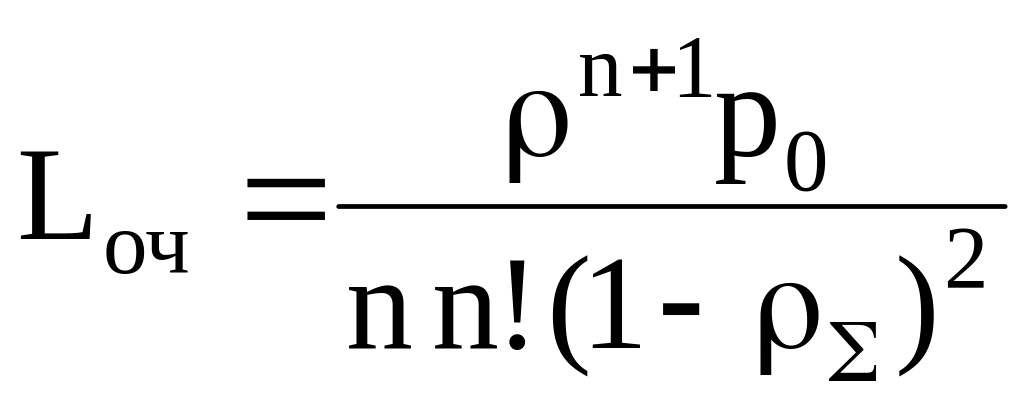
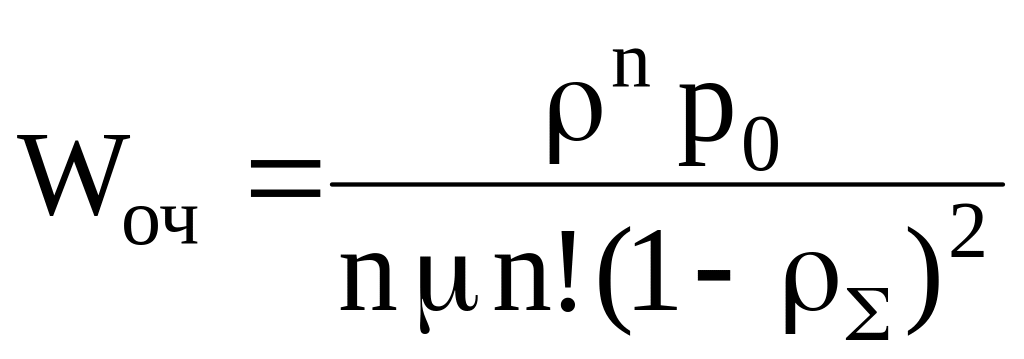
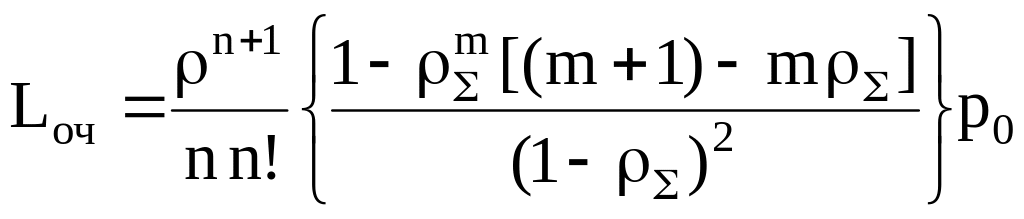
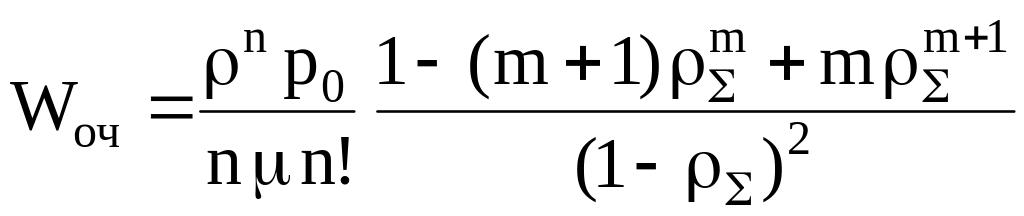
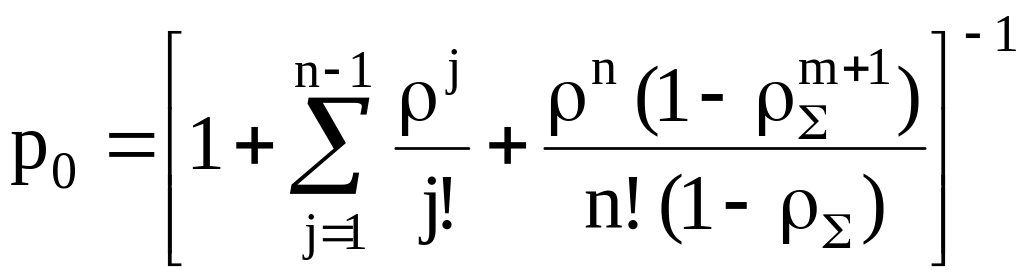
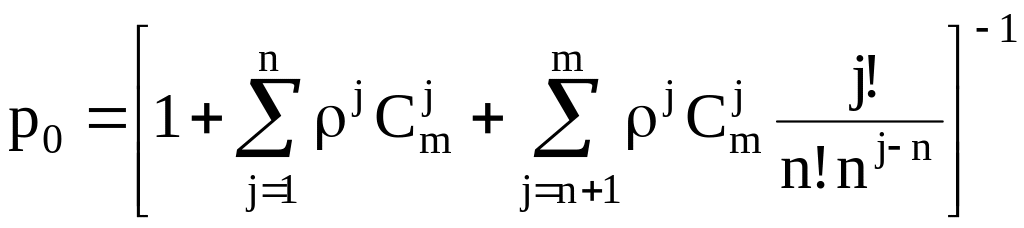 ,
где
,
где
