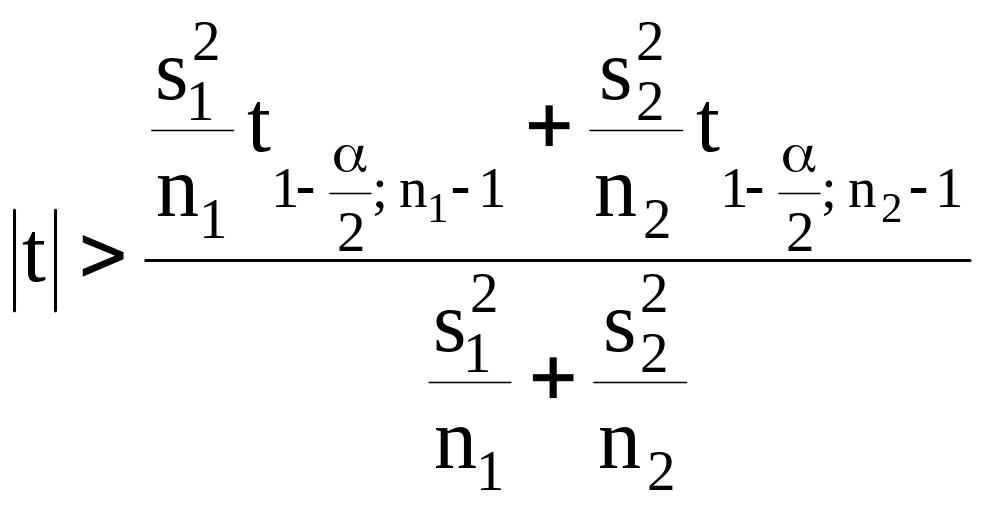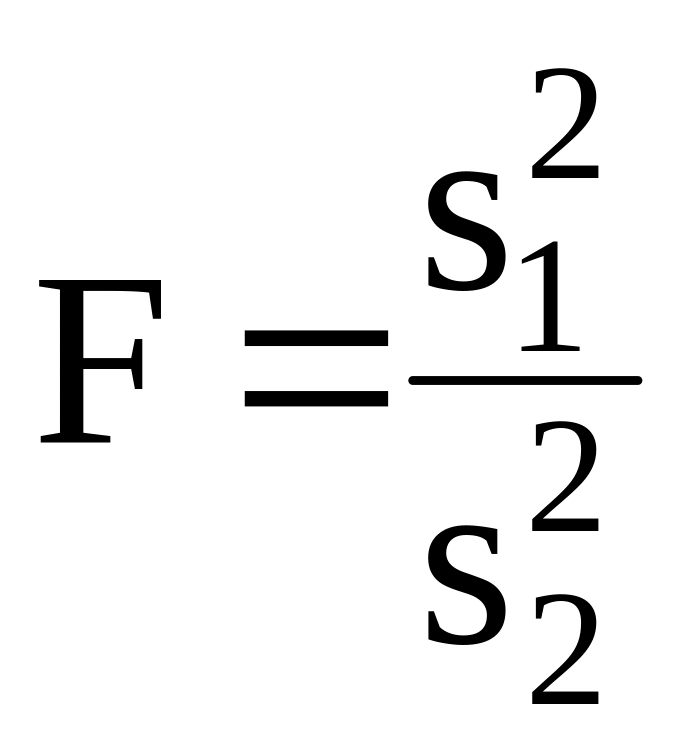8.2.Статистические методы обработки

Для случая исследования сложных систем при большом числе реализаций N в результате моделирования на ЭВМ получается значительный объем информации о состояниях процесса функционирования системы. Поэтому необходимо так организовать в процессе вычислений фиксацию и обработку результатов моделирования, чтобы оценки для искомых характеристик формировались постепенно по ходу моделирования, т.е. без специального запоминания всей информации о состояниях процесса функционирования системы S.

Если при моделировании процесса функционирования конкретной системы S учитываются случайные факторы, то и среди результатов моделирования присутствуют случайные величины. В качестве оценок для искомых характеристик рассчитывают средние значения, дисперсии, корреляционные моменты и т.д.

Пусть в качестве искомой величины фигурирует вероятность некоторого события A. В качестве оценки для искомой вероятности используется частость наступления события , где m — число случаев наступления события A; N — число реализаций. Такая оценка вероятности появления события A является состоятельной, несмещенной и эффективной. В случае необходимости получения оценки вероятности в памяти ЭВМ при обработке результатов моделирования достаточно накапливать лишь число m (при условии, что N задано заранее).

Аналогично при обработке результатов моделирования можно подойти к оценке вероятностей возможных значений случайной величины, т.е. закона распределения. Область возможных значений случайной величины X разбивается на n интервалов. Затем накапливается количество попаданий случайной величины в эти интервалы , . Оценкой для вероятности попадания случайной величины в интервал с номером k служит величина . Таким образом, при этом достаточно фиксировать n значений при обработке результатов моделирования на ЭВМ.

Для оценки математического ожидания СВ X в специальной ячейке памяти фиксируется сумма и находится среднее арифметическое значение:

Оценка дисперсии (8.1) является неудобной для непосредственного вычисления при моделировании, так как в памяти ЭВМ необходимо фиксировать все значения СВ X. Более удобно нахождение оценки дисперсии по формуле

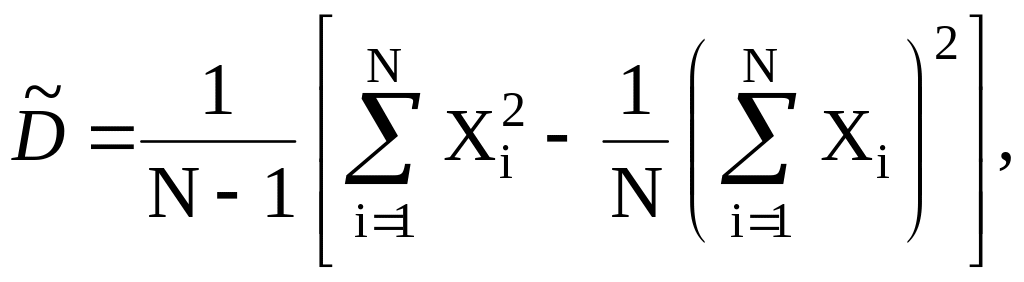
так как для ее определения достаточно фиксировать и .

8.3.Задачи обработки результатов моделирования

При обработке результатов машинного эксперимента с моделью наиболее часто возникают следующие задачи: определение эмпирического закона распределения случайной величины, проверка однородности распределений, сравнение средних значений и дисперсий переменных, полученных в результате моделирования, и т.д. Эти задачи являются типовыми по проверке статистических гипотез. Рассмотрим некоторые из этих задач.

Задача определения эмпирического закона распределения СВ является наиболее общей и требует достаточно большого объема выборок. По результатам испытаний определяются значения выборочной функции и выдвигается гипотеза, что полученное эмпирическое распределение согласуется с тем или иным теоретическим. Проверка гипотезы осуществляется с помощью статистических критериев согласия (Колмогорова, Пирсона и др.). Критерий согласия Колмогорова основан на выборе в качестве меры расхождения U величины . Из теоремы Колмогорова следует, что при имеет функцию распределения

Если вычисленное на основе экспериментальных данных значение меньше, чем табличное значение при выбранном уровне значимости, то гипотезу о согласии принимают, в противном случае расхождение между и считается неслучайным и гипотеза отвергается.

Критерий Колмогорова рекомендуется применять в тех случаях, когда известны все параметры теоретической функции распределения. Неудобство использования критерия связано с необходимостью фиксации в памяти ЭВМ значений всех статистических частот для их дальнейшего упорядочения в порядке возрастания.

При проверке адекватности модели реальной системе возникает необходимость проверки гипотезы, заключающейся в том, что две выборки принадлежат той же генеральной совокупности. Если выборки независимы и законы распределения совокупностей F(u) и F(z), из которых извлечены выборки, являются непрерывными функциями своих аргументов и , то для проверки гипотезы можно использовать критерий согласия Смирнова, применение которого сводится к следующему. По имеющимся результатам вычисляют эмпирические функции распределения и и определяют

.

Затем при заданном уровне значимости находят допустимое отклонение

где и — объемы сравниваемых выборок для и , и проводят сравнение значений D и : если , то гипотезу о тождественности законов распределения и с доверительной вероятностью отвергают.

Сравнение средних значений двух независимых выборок взятых из нормальных совокупностей (дисперсии неравны и неизвестны) сводится к проверке гипотезы : на основании критерия Стьюдента (t-критерия). Проверка по этому критерию сводится к выполнению следующих действий:

Уровень значимости
Статистика
Гипотеза отвергается, если

Представлен приближенный, но вполне приемлемый по точности метод.

Задача сравнения дисперсий сводится к проверке гипотезы, заключающейся в принадлежности двух выборок к одной и той же генеральной совокупности. Алгоритм применения критерия Фишера (проверка гипотезы о равенстве дисперсий двух нормально распределенных случайных величин) следующий:

Уровень значимости
Статистика
Гипотеза отвергается, если

Статистика F представляет собой отношение большей дисперсии к меньшей. В этом случае гипотеза отвергается, если , где — число степеней свободы числителя, а — число степеней свободы знаменателя.

Рассмотренные оценки искомых характеристик процесса функционирования системы S, полученные в результате машинного эксперимента с моделью M, являются простейшими, но охватывают большинство случаев, встречающихся в практике обработки результатов моделирования системы для целей ее исследования и проектирования.