5. Классификация уравнений матфизики

Различают типы уравнений в зависимости от соотношения между коэффициентами.

1) При a=b=c=f=0, d не 0, e не 0 получаем уравнение первого порядка вида

называемое уравнением переноса. Такие уравнения описывают процессы переноса частиц в различных средах, распространение возмущений и т.д. Искомая функция u=u(t,x) зависит от времени и от пространственной переменной, коэффициент p характеризует скорость переноса.

2) Если хотя бы один из коэффициентов a,b,c будет отличен от нуля, то уравнение будет иметь второй порядок и в зависимости от знака дискриминанта

D=b²-4ac

Будет принадлежать к одному из трех типов

D>0 - гиперболическое,

D=0 - параболическое,

D<0 - эллиптическое.

А) Гиперболическое уравнение

Называется волновым, оно описывает различные виды колебаний. Если в уравнение входит одна пространственная переменная, то оно описывает продольные колебания стержня, а также поперечные колебания струны. В этом случае a²=T/ρ, где T - это натяжение струны, а ρ - ее линейная плотность. Двухмерное волновое уравнение используется для описания колебаний тонкой пластины (мембраны)

Трехмерное волновое уравнение

Описывает распространение волн в пространстве (например звуковые волны в различных средах, упругие волны в сплошной среде и т.д.)

Б) параболическое уравнение

называется уравнением теплопроводности или диффузии с помощью него описываются различные процессы, связанные с передачей чего-либо: передачей тепла, передачей импульса, передачей энергии.

В) Эллептическое уравнение

Уравнение Лапласа

Уравнение Пуассона

К уравнениям такого типа приводят стационарные, не зависящие от времени, физические задачи (исследования потенциальных течений жидкости, определение формы нагруженной мембраны и т.д.)

6. Моделирование процесса теплопроводности

В качестве примера модели, в основе которой лежит уравнение матфизики, рассмотрим модель распространения тепла в однородном стрежне. Задача теплопроводности.

Процесс теплопроводности возникает, если тело неоднородно нагрето. Простейшая для изучения теплопроводности система - линейный однородный стержень. В простой модели боковая поверхность стержня считается теплоизолированной, т.е. через нее нет обмена теплом с окружающей средой.

Обозначим температуру стержня в точке с координатой х в момент времени t через u(x,t). Уравнение теплопроводности имеет вид

,

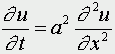где а - коэффициент температуропроводности, зависящий в первую очередь от вещества, из которого сделан стержень.

Уравнение теплопроводности сопровождается начальными и краевыми условиями, делающими постановку задачи физически однозначной Напомню, что если для дифуравнения заданы начальные условия (условия в начальный момент времени), то такая задача называется задачей Коши, если же заданы краевые условия (на границах исследуемой области), то такая задача называется краевой задачей, если заданы и начальные и граничные условия, то мы имеем смешанную краевую задачу. Начальное условие задает распределение температуры в стержне в начальный момент времени (считаем его равным нулю):

u(x,0) = φ(x)

Краевые условия (их должно быть в данном случае два) указывают, в простейшем варианте, какая температура поддерживается на концах стержня:

u(0,t)=ψ₀(t), u(l,t)=ψ_l(t)

Заметим, что начальные и граничные условия должны быть согласованы, т.е.

u(0,0) = φ(0)=ψ₀(0) u(l,0) = φ(l)=ψ_l(0)

Моделирование процесса теплопроводности связано с дискретизацией как временного изменения температуры, так и пространственного.

Введем равномерную прямоугольную сетку с помощью координатных линий

x_i=ih, i=0,1,....n, t_j=jτ, j=0,1,....m,

где h - это шаг по пространству, по координате х, а τ - шаг по времени.

Значения функции в узлах сетки обозначим u_i^j=u(x_i,t_j).

Входящие в уравнение производные заменим их конечно-разностными аппроксимациями

получим

или

,

где i=1,2,:.n-1, j=0,1,:.m-1.

Получилась явная разностная схема, удобная в применении, но устойчивая лишь при выполнении условия

Это следует учитывать, выбирая шаги по времени и пространству.

Совокупность узлов в фиксированный момент времени называется слоем.

Построенная схема позволяет нам находить значение функции температур на j+1 слое через значения на j слое. Для начало счета при j=0 необходимо знать значения функции температур на нулевом слое. Они нам известны из начальных условий.

Если использовать другие конечно разностные соотношения для аппроксимации производных,

то получим существенно более устойчивую неявную схему

или

В отличие от явной схемы каждое разностное уравнение второй схемы содержит на каждом новом слое три неизвестные значения, которые невозможно определить сразу же, как мы поступали в явной схеме. При этом вторая разностная схема состоит из линейных трех точечных уравнений, т.е. каждое уравнение содержит неизвестную функцию в трех точках нового слоя. Такие системы линейных уравнений, системы с трехдиагональной матрицей, могут быть легко решены методом прогонки. Таким образом, в случае неявной схемы, чтобы посчитать значения функции температур в каждый следующий момент времени, т.е., чтобы перейти на следующий слой по времени, необходимо каждый раз решать методом прогонки линейную систему.

Это - система линейных алгебраических уравнений с трехдиагональной матрицей. Для ее решения наиболее эффективен метод прогонки.

Так можно моделировать физические явления применяя математический аппарат во всей его мощи. Однако это довольно сложно. При моделировании явления теплопроводности можно пойти другим путем.

Пусть задана квадратная пластина, на краях которой известна температура. Требуется определить температуру во внутренних точках. Если предположить, что теплоотвода внутри нет, то можно смоделировать решение путем вычисления среднего значения T=(t1+t2+t3+t4)/4.

Однако это очень грубое приближение, ведь в разных точках пластины температура различна.

Разобьем квадрат на четыре части и для каждого малого квадратика применим ту же процедуру:

T11 = (t1 + T12 + T21 + t4)/4 T12 = (t1 + T11 + T22 + t2)/4 T21 = (t4 + T11 + T22 + t3)/4 T22 = (t2 + T21 + T12 + t3)/4

Или в другом виде

4T11 - T12 - T21 = t1 + t4 -T11 + 4T12 - T22 = t1 + t2 -T11 + 4T21 - T22 = t3 + t4 -T12 - T21 + 4T22 = t2 + t3

который представляет систему линейных уравнений относительно неизвестных T11, T

Модели биологических и экологических систем. Моделирование в биологии, химии, медицине, экологии. Принципы выбора объектов для моделирования. Модели распространения эпидемий и динамики развития популяций.