
- •1 Функция. Постоянные и переменные величины. Одз. График ф-ий. Способы задания ф-ий.
- •2 Сложная,обратная,неявная ф-ии. Четная и нечетная ф-ия. Периодическая ф-ия. Ограниченная ф-ия.
- •3 Предел ф-ии. Определение. Геометрический смысл предела.
- •5 Теорема3,следствие,4,5.
- •6 Односторонние пределы. Определение предела слева и предела справа.
- •7 Бесконечно малые и бесконечно большие величины. Теоремы о бесконечно малых. Теорема1.
- •8 Теорема 2. Следствия 1,2,3. Замечание об отношении 2б.М.
- •9. Теоремы о пределах. Теоремы1,2,следствие,3.
- •10. Теорема4(предел частного)
- •12 Первый замечательный предел.
- •13 Число е. Второй замечательный предел и его следствия.
- •15 Теоремы о непрерывных ф-ях. Теорема1,2,3,4
- •16 Типы точек разрыва. Устранимый разрыв. Разрывы 1,2 рода. Скачок.
- •17 Производная. Геометрический и механический смысл. Уравнение касательной.
- •18 Зависимость между непрерывностью и диф-тью ф-ий.
- •20 Производные обратных тригонометрических ф-ий.
- •21 Производная сложной ф-ии.
- •26 Геометрический смысл диф-ла.
- •27 Применение дифференциала к приближенным вычислениям.
- •28. Приложение производной. Теорема Ферма. Ее геометрический смысл.
- •29.Теорема Роля.
- •30.Теорема Коши.
- •31.Теорема Лагранжа.Ее геом смысл.Следствия1,2.
- •32.Правило Лоиталя.Теорема.
- •33.Возрастание и убыв ф-ии.
- •Часть 2 док-ть сам-но
- •34.Экстремумы ф-ии. Теорема3.
- •35.Теоремы 4,5.
- •36.Теорема6.
- •37.Выпуклость и вогнутость ф-ии.Теорема7.
- •38.Точка перегиба.Теорема8.
- •42. Таблица неопределенных интегралов
- •47. Приближенное вычисление определенных интервалов
- •48. Несобственные интегралы.
- •49. Разложение многочлена по формуле Тейлора.
- •51. Экстремум ф-ии нескольких переменных
- •52. Метод наименьших квадратов.
- •56. Д/у II порядка.Понижение порядка д/у.
- •57.Линейные д/у II порядка.Линейная независ ф-ий.Критерий лин. Независимости.
- •58.Теорема1(об общем реш-ии лин однор-го д/у II порядка).
- •59.Лин однор-ое д/у с постоянными коэффициентами.
- •60.Теорема2(общем реш-ии лин неоднор-го д/у II порядка).
- •61.Линейные неоднородные д/у II порядка с пост. Коэфициентами.
51. Экстремум ф-ии нескольких переменных
Определение
М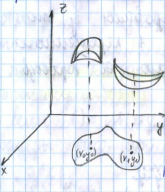 аксимумом
ф-ии
называется такое ее значение f(x0,y0)
которое является наибольшим в некоторой
окрестности точки M(x0,y0).
Аналогично, минимумом ф-ии
называетмя такое ее значение f(x1,y1)
которое является наименьшим в некоторой
окрестности точки M(x1,y1)
аксимумом
ф-ии
называется такое ее значение f(x0,y0)
которое является наибольшим в некоторой
окрестности точки M(x0,y0).
Аналогично, минимумом ф-ии
называетмя такое ее значение f(x1,y1)
которое является наименьшим в некоторой
окрестности точки M(x1,y1)
Максимумы и минимумы ф-ии называются экстремумами ф-ии, а точки в которых достигаются экстремумы называются точками экстремума ф-ии.
Теорема 1 (необходимый признак)
Если в точке M(x0,y0) дифференцируемая ф-ия достигает экстремума, то ее частные производные в этой точке равны нулю.
Док-во
Для доказательства зафиксируем и положив
y=y0
получим ф-ию
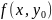 которая зависит только от x
которая зависит только от x
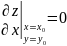
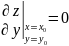 (к дано)
(к дано)
Когда мы зафиксировали y то получили ф-ию от 1 переменного v по необх условию ее производная равна 0
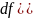
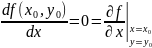
Если x=x0 то f(x0,y)

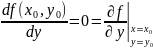
Такие как и для ф-ии 2-х независимых переменных если ф-ия f(x,y,z) дифференцируема и имеет в точке (x0,y0,z0) то
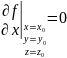
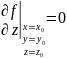
Точка M(x0,y0) в которой частные производные обращаются в 0 называется стационарной точкой
Теорема 2(достаточный признак экстремума)
Если точка M(x0,y0) есть стационарная точка дважды дифференцируемой ф-ии
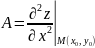
 -
смешанная производная в точке M
-
смешанная производная в точке M
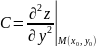 -
значение производной по y
в точке M
-
значение производной по y
в точке M
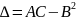
>0 то экстремум есть, причем если A>0 – min, A<0 – max
<0 экстремума нет
=0 требуется дополнительное исследование ибо никакое заключение о характере стационарной точки сделать не можем.
52. Метод наименьших квадратов.
Пусть мы хотим найти зависимость между 2-мя величинами x и y значения которых помещены в таблицу.
X |
X1 |
X2 |
. |
. |
. |
Xn |
y |
Y1 |
Y2 |
. |
. |
. |
yn |
Рассмотрим x и y как прямоугольные координаты. Нанесем их на координатную плоскость. Будем полагать что точки почти лежат в некоторой прямой
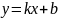 (1)
(1)
Где k и b параметры подлежащие определению.
Для удобства примем (1) в виде (2) kx+b-y=0. При подстановке в (2) вместо x и y их значения из таблицы, поскольку точки лишь приблизительно лежат на прямой получим (3)
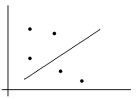
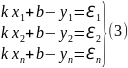
Где
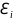 – некоторые числа которые мы будем
называть невязками. Они могут иметь
различные знаки. При способе наименьших
квадратов k и b
подбирают таким образом чтобы сумма
квадратов этих невязок была наименьшей,
т.е. составляют ф-ию
– некоторые числа которые мы будем
называть невязками. Они могут иметь
различные знаки. При способе наименьших
квадратов k и b
подбирают таким образом чтобы сумма
квадратов этих невязок была наименьшей,
т.е. составляют ф-ию
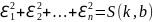
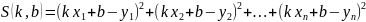 - есть ф-ия 2-х переменных k
и b которые подберем так,
что бы S получило возможно
наименьшее значение. Пользуясь необх
усл экстремума видим, что для этого
должно выполняться
- есть ф-ия 2-х переменных k
и b которые подберем так,
что бы S получило возможно
наименьшее значение. Пользуясь необх
усл экстремума видим, что для этого
должно выполняться

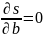
Так
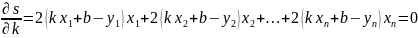
Сокращаем на u группируя относительно k и bполучим
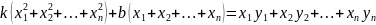
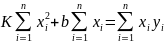
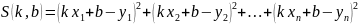
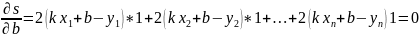
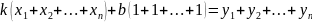
Для нахождения k и b получается простая система (4) 2-х уравнений 1-ой степени с 2-мя неизвестными
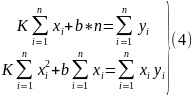
53. простейшие дифференциальные уравнения.
Дифференциальным (обыкновенным) уравнением называется соотношение связывающее независимую переменную, ф-ию и ее производные различных порядков от одного и того же аргумента x.
Часто д.у. записывается в виде разрешенном относительно старшей производной.
Порядком д.у. называется порядок старшей производной.
Общим
решением д.у. n-го порядка является ф-ия
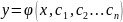 определенная в некотором интервале
(A;B) обращающая д.у. в тождество и содержащее
столько независимых производных
постоянных Ci каков порядок д.у.
определенная в некотором интервале
(A;B) обращающая д.у. в тождество и содержащее
столько независимых производных
постоянных Ci каков порядок д.у.
Термин «незав произв постоянные» означает что число их не может быть уменьшено путем введения новых независимых производных постоянных.
Частичным решением д.у. называется решение д.у. получаемое из общего при определенных значениях производных постоянных входящих в общее решение
Общий интеграл д.у. называется общее решение д.у. записанное в неявном виде.
Д.у. первого порядка.
Д.у. 1-го порядка называется соотношение связывающее независимую переменную ф-ии и ее производную.
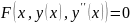
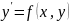 (3)
(3)
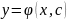
Задача Коши.
Пусть дано д.у. (3) и требуется найти решение этого уравнения удовлетворяющее начальному условию
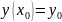 (5)
(5)
Таким образом задача Коши состоит в нахождении решения уравнения (3) удовлетворяющего начальному условию (5).
График решения д.у. называется интегральной кривой. Учитывая это можно сформулировать геометрический смысл задачи Коши. Найти интегральную кривую уравнения (3) проходящую через точку (x0,y0)
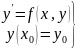
(x0,y0)
Теорема Коши (существования и единственности)
Пусть в уравнение (3) ф-ия f(x,y) определена и непрерывна в некотором прямоугольнике R содержащим
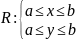
(x0,y0) є R
Частная производная
 непрерывна тогда уравнение
непрерывна тогда уравнение
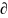 имеет единственное решение проходящее
через точку (x0,y0)
имеет единственное решение проходящее
через точку (x0,y0)
Задача интегрального исчисления y’=f(x) где f(x) – известно, а y – неизвестно является простейшим д.у. имеющим решение без задачи.
Решение содержит одну производную постоянную т.е. является однопараметрическим семейством.
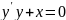

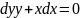
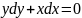
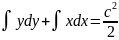
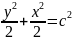
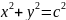
54. Д.у. с разделенными переменными
Одни
имеют вид
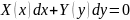 (6) где при дифференциалах dx и dy стоят
соответственно ф-ии только от x или
только от y.
(6) где при дифференциалах dx и dy стоят
соответственно ф-ии только от x или
только от y.
Пусть
F(x) – первообразная ф-ии X(x) а ф-ия G(x) –
ф-ии Y(y) тогда общий интеграл уравнения
(6) имеет вид
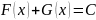 (7)
(7)
Док-во.
Пусть y=y(x) – решение уравнения (6) тогда при подстановке в (6) оно обращает его в тождество
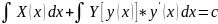
Или
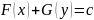
Мы
получим общий интеграл уравнения.
Посмотрим в каком случае можно получить
общее решение уравнения. Пусть G’(y)
отлично от 0, т.е.
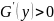 - ф-ия возрастает,
- ф-ия возрастает,
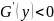 - ф-ия убывает, но она монотонна. Поскольку
она дифференцируема то по т о независимости
между диф-ю и непрерывностью она
непрерывна.
- ф-ия убывает, но она монотонна. Поскольку
она дифференцируема то по т о независимости
между диф-ю и непрерывностью она
непрерывна.
Д.у. с разделяющимися переменными.
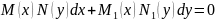 (8)
(8)
Где
при дифференциалах dx и dy стоит произведение
ф-ий одна из которых зависит только от
x, 2-ая только от y. Для решения произведения
(8) разделим его на
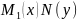
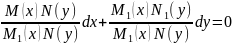
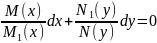 (9)
(9)
Уравнение (9) уравнение с разделенными переменными и его общий интеграл имеет вид
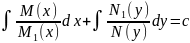 (10)
(10)
В результате деления могут быть потеряны решения:
Если x=a, то M1(x)=0, M1(a)=0
Если y=b, то N(y)=0, N(b)=0
X=a, x=b является решениями подозрительными на особые. Они будут особыми решениями если не получаются из (10) не при каких произв пост С. В этом случае их через запятую прибавляют к (10)
55. линейное дифференцированное уравнение 1-го порядка
Им является уравнение (11)
 (11)
(11)
Которое содержит ф-ию и ее производную в первой степени и не содержит их производные
P(x) и g(x) – непрерывны
Если
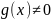 то уравнение (11) называется линейным
неоднородным 1-го порядка, если
то уравнение (11) называется линейным
неоднородным 1-го порядка, если
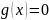 то уравнение имеет вид
то уравнение имеет вид
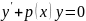 и называется линейное однородное д.у.
1-го порядка
и называется линейное однородное д.у.
1-го порядка
Для решения уравнения (11) сделаем подстановку y=uv где u(x) – независ ф-ия, а v(x) – некоторая ф-ия которую мы определим в дальнейшем.
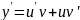 - подставим производную в (11)
- подставим производную в (11)
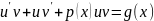
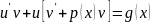 (13)
(13)
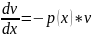
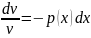
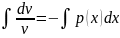

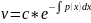 c=1
c=1
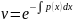
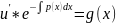
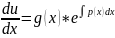
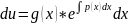
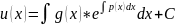
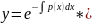
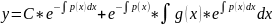 (14)
(14)
