27 Применение дифференциала к приближенным вычислениям.

Из определения дифференциала следует что df так же как и Δf → 0, когда Δx→0, т.е. df и Δf бесконечно малые когда Δx→0.

Сравним эти бесконечно малые

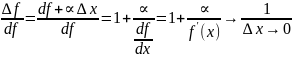
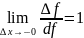
Значит дифференциал эквивалентен приращению ф-ии когда Δx→0. Значит можно брать приближенно в качестве приращения ф-ии ее дифференциал

28. Приложение производной. Теорема Ферма. Ее геометрический смысл.

Пусть ф-ия y=f(x) принимает свое наибольшее и наименьшее значение во внутренней точке ξ промежутка (a;b). a<ξ<b тогда если в точке ξ производная ф-ии y=f(x) существует то она равна нулю f’(ξ)=0.

Док-во.

Пусть для определенности в точке ξ ф-ия принимает наибольшее значение f(ξ+Δx)≤f(ξ) тогда

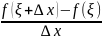(13)

числитель в (13) неположителен, если Δx>0 то дробь (13)≤0, но мы знаем что если ф-ия неотрицательна то и предел ее неотрицательный

2. ∆x<0

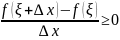
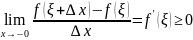
т.к. по условию теоремы в точке ξ производная существует то пределы слева и справа равны => f’(ξ)=0 док-ть сам-но???????

Геометрический смысл теоремы.

Касательная к графигу ф-ии в наивысшей и наинизшей внутренней точке параллельна оси OX.

29.Теорема Роля.

Если ф-ия y=f(x) непрерывна на отрезке [A;B], дифференцируема во всех его внутренних точках и f(a)=f(b) то существует хотя бы 1 значение x=c (c є [a;b]) в которой производная равна нулю. F’(c)=0. возможны 2 случая: 1. наиб и наим значения ф-ии принимает на концах отрезка [a;b]

Наим →m=f(a)=f(b)=M →наиб

В этом случае ф-ия y=f(x) принимает постоянные значения во всех точках отрезка [a;b] т.е. она постоянна и значит ее производная равна нулю всюду на отрезке [a;b].

2. ф-ия изменяется и будучи непрерывной в замкнутом интервале она (по св-ву) принимает свое наиб и наим значение причем хотя бы 1 значение принимается ф-ей внутри [a;b]. Ф-ия по условию теоремы дифференцируема во всех внутренних точках, а значит и в точке в которой она принимает наим или наиб значение тогда по теореме Ферма производная в такой точке равна нулю.

30.Теорема Коши.

Пусть ф-ии f(x) b φ(x) непрерывны на [a;b] дифференцируемы во всех его внутренних точках причем φ’(x)≠0 в этих точках тогда по интервале (a;b) существует хотя бы 1 точка ξ в которой выполняется равенство:

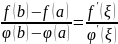(14)

Если бы φ(b)=φ(a) то существовала бы хотя бы 1 точка внутри интервала (a;b) в которой производная φ’(x)=0. этого быть не может т.к. вступает в противоречие с условием теоремы.

Составим вспомогательную ф-ию

F(x)=f(x)-kφ(x) (15)

Где k – неизвестно. Эта ф-ия должна удовлетворять всем условиям теоремы Роля:

1. непрерывна на [a;b]

2. дифференцируема в интервале (a;b)

3. подберем k так чтобы F(a)=F(b).

f(a)-kφ(a)=f(b)=kφ(b)

K=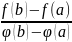

F(x)=f(x)-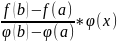

При последней ф-ии выполняется все условия т.Ролля значит существует x=ξ в которой производная равна нулю.

x=ξ

F(x)=f(x)-

F’(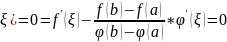

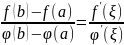
Замечание

В частности если φ(x)=x то т.Коши совпадает с т.Лагранжа.

31.Теорема Лагранжа.Ее геом смысл.Следствия1,2.

Если ф-ия f(x) непрерывна в замкнутом интервале (a;b) дифференцируема во всех внутренних точках то существует такая точка c в которой выполняется равенство:

f(b)-f(a)=(b-a)*f’(c) (16) док-ть сам-но???????

Геометрический смысл т. Лагранжа.

A(a;f(a))

B(b;f(b))

На графике ф-ии провели секущую AB через точки A(a;f(a)) и B(b;f(b)). Будем секущую AB перемещать параллельно себе до тех пор пока она не станет касательной NKT к графику ф-ии. Если прямые AB и NT параллельны, то их угловые коэффициенты равны

K_кас=f’(c)

K_{секущей}=tgφ=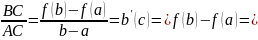

Следствие (к т. Лагранжа)

1. для того чтобы производная ф-ии равнялось нулю необходимо и достаточно чтобы ф-ия была тождественна постоянной на этом промежутке

2. для того чтобы 2 ф-ии имели равные производные необходимо и достаточно чтобы они отличались друг от друга самое большее на постоянное слагаемое.

Необходимость: пусть ф-ии f(x) и g(x) имеют в промежутке равные производные f’(x)=g’(x). Докажем что f(x)=g(x)+c введем ф-ю F(x)=f(x)-g(x) ее производная F’(x)=f’(x)-g’(x)=0, тогда F(x)=const=c=f(x)-g(x)=>f(x)=g(x)+c

Достаточность: если 2 ф-ии отличаются на постоянное слагаемое, то их производные равны док-ть сам-но???????