56. Д/у II порядка.Понижение порядка д/у.

Случай1.Когда д/у не содержит ф-ию,т.е. имеет вид F(x,y`,y``)=0.В этом случае делается подстановка y`=Р,где Р=р(х) ; y``=Р`,где … и ур-ие сводится к ур-ию I порядка.

Φ(х,р,dp/dx)=0,где р ф-ия,а х-аргумент.Пусть рещ-ие ур-ия Φ(х,р,dp/dx)=0 имеет вид

Р(х)=φ(х,С₁) ; Р(х)=у`(x)=φ(х,С₁),тогда у(х)=∫φ(х,С₁)dx+c.

Случай2.Ур-ие не содержит явно независ переменную,т.е. имеет вид F(у,y`,y``)=0. Делаем подстановку y`=Р,но р=р(у),тогда y``=dp/dy*dy/dx=dp/dy*p и ур-ие F(у,y`,y``)=0 преобретает вид Φ(у,р,dp/dу*р)=0- д/у I порядка,где р яв-ся ф-ия,у-аргумент. Реш-ие ур-ия р(у)=Ψ(у,с₁),но y`(х)=р(у)=Ψ(у,с₁) ; dy/dx=Ψ(у,с₁) ; dy/ Ψ(у,с₁)=dx ; общий интеграл имеет вид ∫dy/ Ψ(у,с₁)=x+с₂

Случай3. y``=f(х),тогда y`=∫f(х)dх+с₁ ; у(х)=∫(∫f(х)dх)dх +с₁х+с₂общее реш-ие исхожного д/у II порядка(нужно дважды проинтегрировать по х)

57.Линейные д/у II порядка.Линейная независ ф-ий.Критерий лин. Независимости.

Лин д/у II порядка имеет вид : y``+p(x)у`+g(x)y=f(х) (7),где p(x),g(x) и f(х)-непрерыв ф-ии, если f(х)≠0,то ур-ие y``+p(x)у`+g(x)y=f(х) назыв «лин неоднор-ое д/у II порядка».Если f(х)≡0,то ур-ие имеет вид y``+p(x)у`+g(x)y=0-«лин однор-ое д/у II порядка». Пусть у₁(х) и у₂(х)-частные лин-но независ решения ур-ия(7).Ф-ии у₁(х) и у₂(х)-назыв лин зависимыми, если сущ-ют такие соnst с₁ и с₂ не обе равные нулю,что выполняется равенство

с₁у₁(х)+с₂у₂(х)=0.

Критерий лин незав-сти.Для того,чтобы ф-ии были лин зависимы необх и достат-но, чтобы они были пропорциональны.

Необходимость.Дано,что ф-ии лин зависимы.Док-ть,что они пропорциональны.Если ф-ии лин зависимы,то выполняется с₁у₁(х)+с₂у₂(х)=0,где с₁ и с₂ неодновременно равны нулю. Пусть с₁≠0,тогда у₁(х)=kу₂(х),где k= -с₂/с₁,т.е. ф-ии пропорциональны.

Достаточность.Дано,что ф-ии пропорциональны,док-ть,что они лин зависимы.Если ф-ии пропорциональны, то у₁(х)=kу₂(х),а это и есть с₁у₁(х)+с₂у₂(х)=0,где с₁=1,а с₂= -k.

58.Теорема1(об общем реш-ии лин однор-го д/у II порядка).

Пусть у₁(х) и у₂(х) часные лин-но независ реш-ия ур-ия y``+p(x)у`+q(x)y=0,тогда общее реш-ие однор ур-ия имеет вид у_оо=с₁у₁(х)+с₂у₂(х) (11),где с₁ и с₂ произвольные соnst.

Док-во:т.к. у₁(х) и у₂(х) частные реш-ия ур-ия y``+p(x)у`+g(x)y=0,то выполняется

y_i``+p(x)y<sub>i</sub>`+q(x)y<sub>i</sub>≡0(i=1,2).Подставим (11) в y``+p(x)у`+g(x)y=0 :

(с₁у₁+с₂у₂)``+p(x)(с₁у₁+с₂у₂)`+q(x)(с₁у₁+с₂у₂)=раскроем скобки и сгруппируем подобные=

с₁(y₁``+p(x)у<sub>1</sub>`+q(x)y<sub>1</sub>)+с<sub>2</sub>(y``+p(x)у`+g(x)y)≡0 ; с<sub>1*</sub>0+с<sub>2*</sub>0≡0,т.е.(11) есть реш-ие ур-ия y``+p(x)у`+q(x)y=0,но нам необх-мо док-ть,что реш-ие яв-ся общим.

Замечание.требование лин-ой независ-ти ф-ий у₁(х) и у₂(х) яв-ся существенным для док-ва того,что реш-ие будет общим.

Действительно,если бы у₁(х) и у₂(х) были лин завис-мы,то по критерию они были бы пропорциональны у₁(х)=kу₂(х),тогда у_оо=с₁kу₂+с₂у₂=у₂(с₁k+с₂)=с₃у₂, с₃=с₁k+с₂. Реш-ие содержало бы 1 произвольную пост и значит не было бы общим реш-ем д/у II порядка, потому что лин д/у II порядка должно содержать две независ произвольные соnst.

59.Лин однор-ое д/у с постоянными коэффициентами.

Они имеют вид y``+p(x)у`+q(x)=0,где р и q-пост числа.(будем искать реш-ие ур-ия в виде у=e<sup>kx</sup>,где k-неизвестное пока число);y`=ke<sup>kx</sup> ; y``=k²e^kx ; k²e^kx+рke^kx+qe^kx=0 ; e^kx(k²+рk+q)=0

Поскольку e^kx≠0,то k²+рk+q=0-характеристическое ур-ие ур-ия y``+p(x)у`+q(x)=0,его корни k₁ и k₂ находятся по формуле 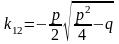,найдя корни харак-го ур-ия мы найдем частные реш-ия.

Случай1. p²/4-q>0,в этом случае k²+рk+q=0 имеет корни действительные,различные k₁≠k₂, тогда у₁(х)=e^k1x ; у₂(х)=e^k2x ; у_оо=с₁у₁+с₂у₂ –мы показали,что у₁(х),у₂(х)–лин-но независимы,

Если k₁≠k₂,тогда общее реш-ие имеет вид: у_оо=с₁e^k1x +с₂e^k2x

Случай2. p²/4-q=0,в этом случае k₁=k₂= -р/2.Корни одинаковые.В этом случае

у₁(х)=e^-р/2*x.Будем отыскивать у₂(х) в виде z(x)у₁(х)=z(x)e^-р/2*x,при этом z(x)≠соnst.

Итак, у₂`(х)=z`(x)e^-р/2*x-I производная.Теперь нужно найти II.

y₂``(x)=z``(x)e^-р/2*x-p/2*z`(x)e<sup>-р/2*x</sup>-p/2*z`(x)e^-р/2*x+p²/4*z(x)e^-р/2*x=

=z``(x)e<sup>-р/2*x</sup>-pz`(x)e<sup>-р/2*x</sup>+p<sup>2</sup>/4*z(x)e<sup>-р/2*x</sup> .Подставим в y``+p(x)у`+q(x)y=0.

z``e^-р/2*x-рz`e<sup>-р/2*x</sup>+ p<sup>2</sup>/4*ze<sup>-р/2*x</sup>+рz`e^-р/2*x- p²/2*ze^-р/2*x+qze^-р/2*x=0

z``e<sup>-р/2*x</sup>+(q- p<sup>2</sup>/4)ze<sup>-р/2*x</sup>=0.Но (q- p<sup>2</sup>/4)=0 по условию.=> z``(x)e^-р/2*x=0 => z``=0,тогда z`(х)=а, z(х)=ах+b, где а и b-пост числа,к-ми мы можем распорядиться по своему усмотрению.Возьмем а=1, b=0,тогда z(х)≡х и у₂(х)=хe^-р/2*x,тогда у_оо=с₁e^-р/2*x+с₂хe^-р/2*x.

Случай3. p²/4-q<0,тогда q- p²/4>0.И обозначим q- p²/4=β² ; k₁₂=- p/2±β_i ;

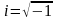; i²=-1(мнимая единица) ; е^iβx=cosβx+isinβx-формула Эйлера.Реш-ие в этом случае будет записываться: у₁(х)=e^-р/2*xcosβx ; у₂(х)=e^-р/2*xsinβx ; у_оо=с₁e^-р/2*xcosβx +с₂e^-р/2*xsinβx.

с₁ и с₂ –произвольные постоянные,вообще говоря комплексные.