2. Гиперплоскости в пространстве

Аффинное множество в пространстве , размерность которого равна , называется гиперплоскостью.

В пространстве прямые являются гиперплоскостями. В самом деле, размерность направляющего подпространства прямой равна единице. Следовательно, где

В пространстве плоскости являются гиперплоскостями. Действительно, размерность направляющего подпространства плоскости равна двум. Отсюда где

□Теорема 2.20. Справедивы следующие утверждения.

1.Ненулевой вектор перпендикулярен гиперплоскости тогда и только тогда, когда . Ненулевые векторы и , перпендикулярные гиперплоскости , коллинеарны.

2. Множество решений уравнения , является гиперплоскостью, перпендикулярной вектору .

Доказательство.

1. Так как

,

то . Если же , то . Отсюда следует, что векторы и коллинеарны.

2. Из теоремы 2.13 следует, что , т.е. гиперплоскость, а из теоремы 1.24 получаем, что . Теперь из первого утверждения теоремы вытекает .■

Ненулевой вектор , перпендикулярный гиперплоскости, называется нормальным вектором гиперплоскости.

□ Теорема 2.21. Справедливы следующие утверждения.

1 Уравнение

является уравнением гиперплоскости тогда и только тогда, когда гиперплоскость проходит через точку параллельно линейно независимым векторам .

2. Уравнение

является уравнением гиперплоскости тогда и только тогда, когда гиперплоскость проходит через точку перпендикулярно ненулевому вектору .

Доказательство следует из теорем 2.15 и 2.16, в формулировке которых .■

задачи

1. Найти точку пересечения гиперплоскости 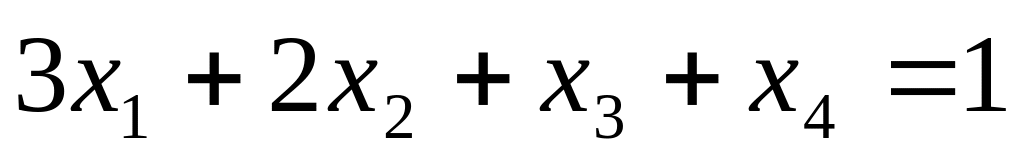и прямой, проходящей через точку (1, 1, 1, 1) параллельно вектору .

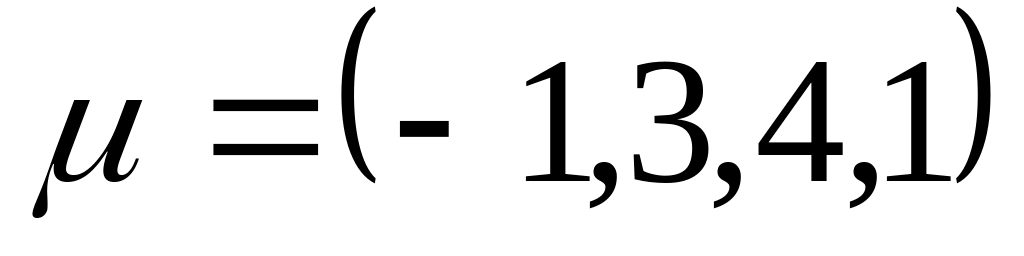2. Доказать, что каждая прямая является пересечением конечного числа гиперплоскостей.

3. Доказать, что гиперплоскост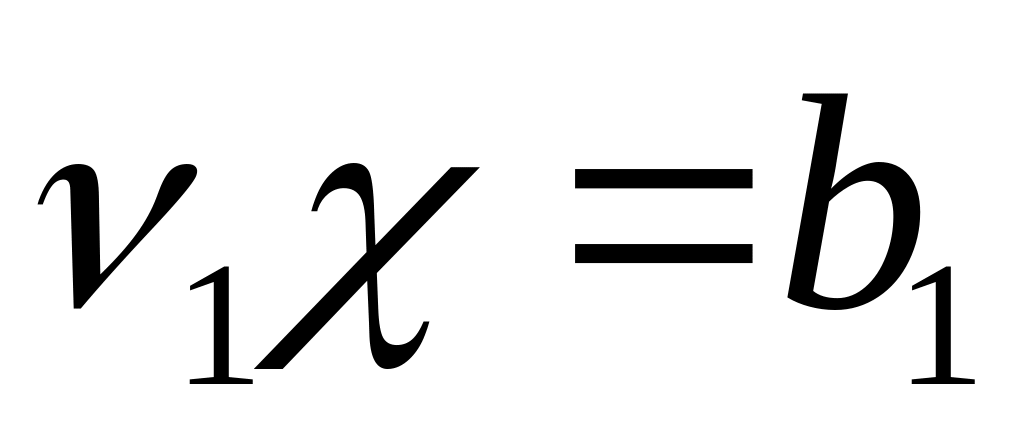и и 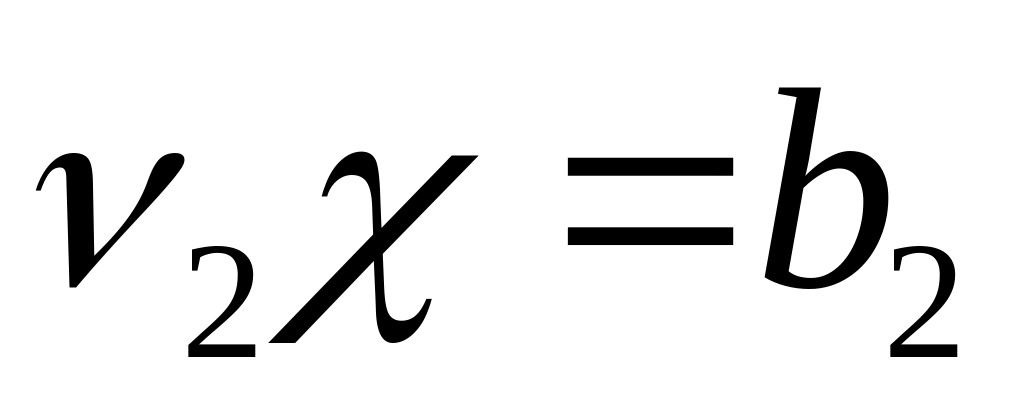совпадают тогда и только тогда, когда они имеют общую точку и .

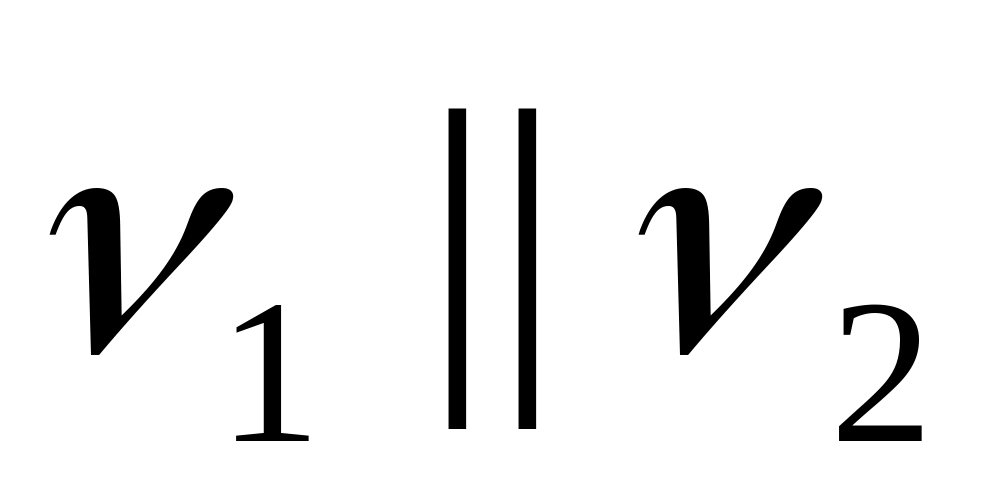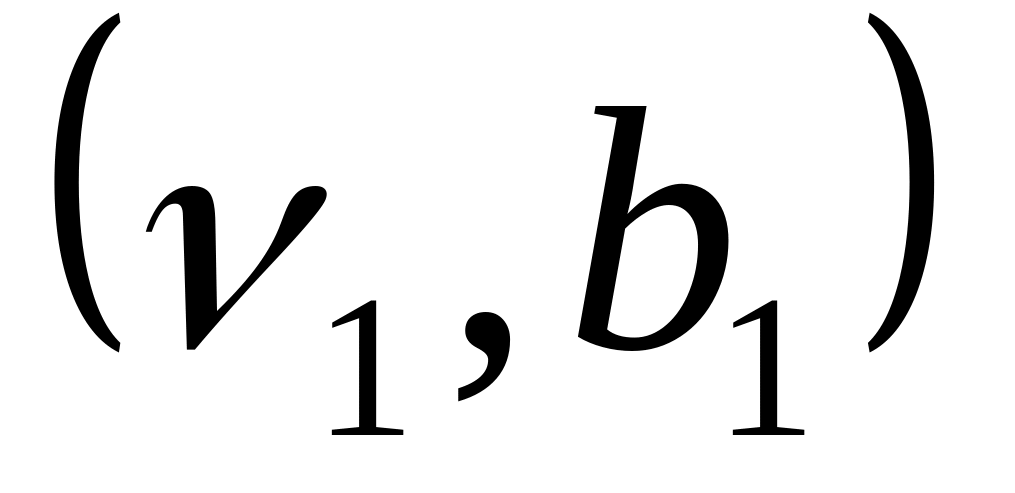4. Доказать, что гиперплоскости и не имеют общих точек тогда и только тогда, когда , а векторы и 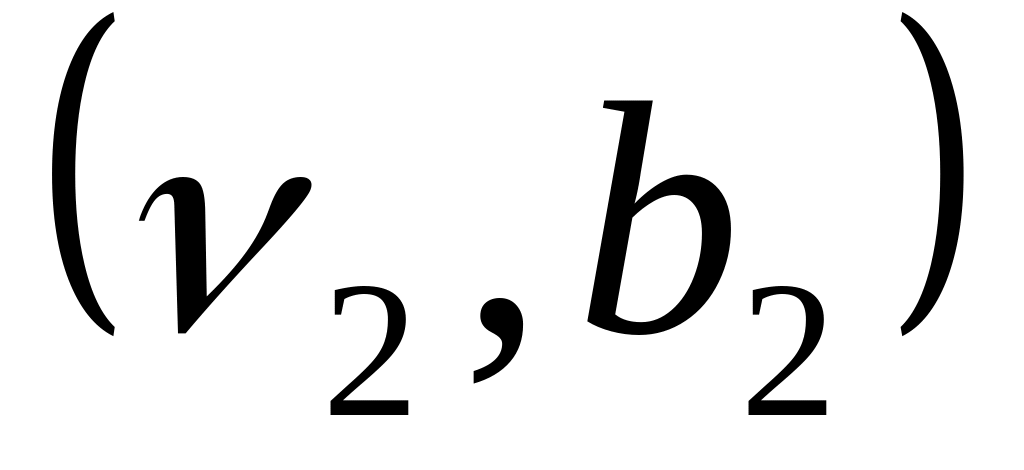не коллинеарные.

5. Доказать, что пересечение двух гиперплоскостей в пространстве 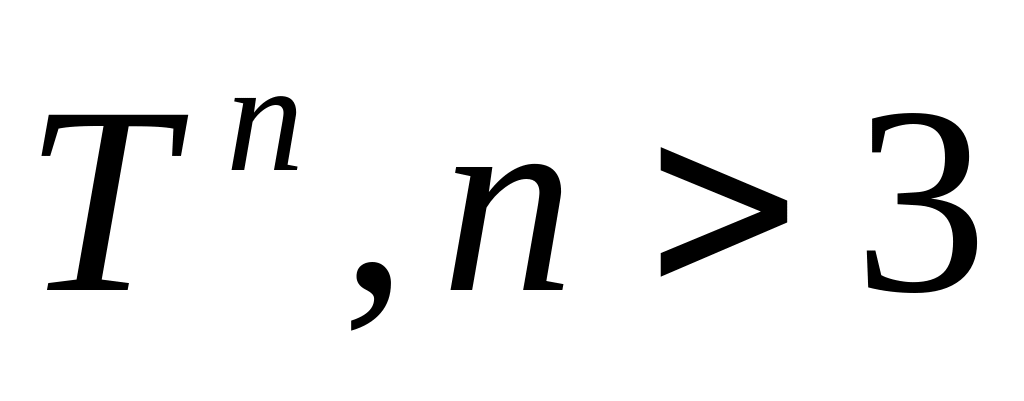, не является прямой.

6. Доказать, что прямая и гиперплоскость не пересекаются тогда и только тогда, когда 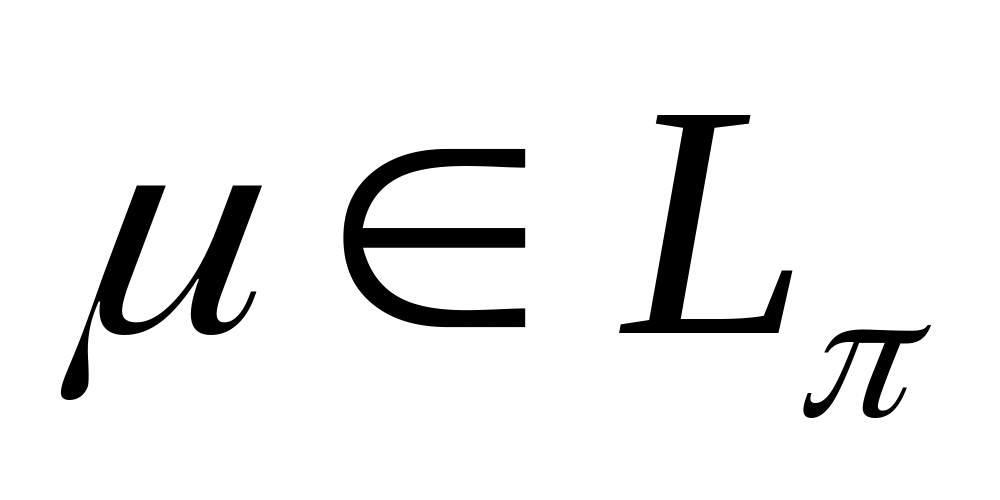и .

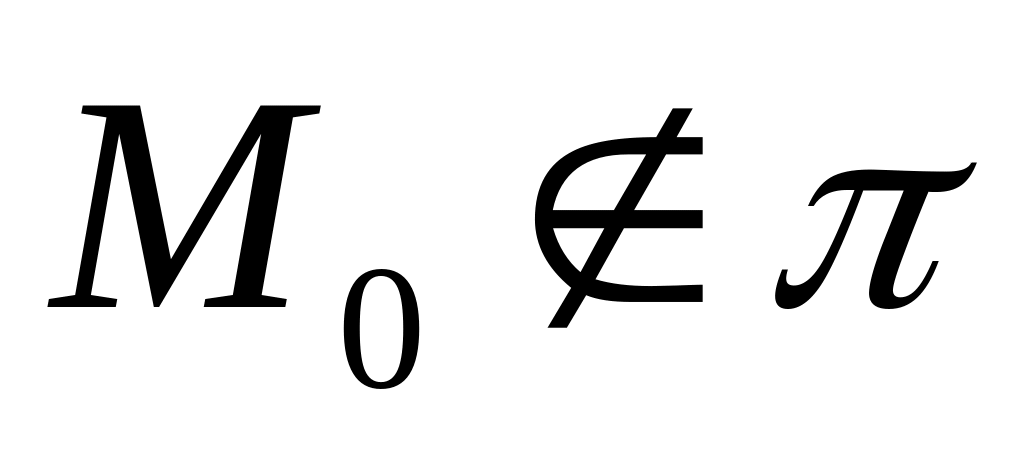7. Доказать, что каждое аффинное множество размерности k можно задать как пересечение 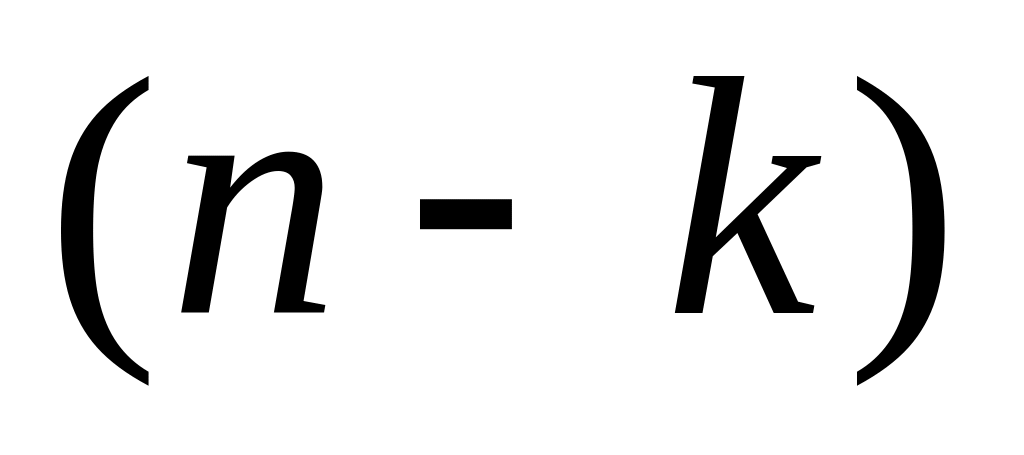гиперплоскостей.

8. Доказать, что уравнение гиперплоскости , проходящей через точку имеет вид 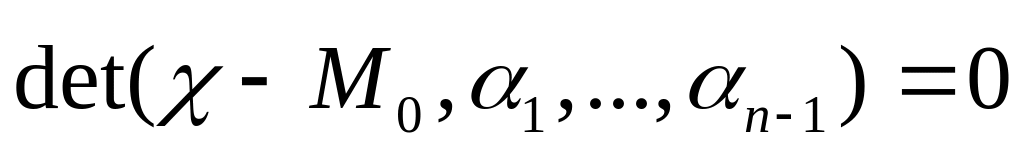, где 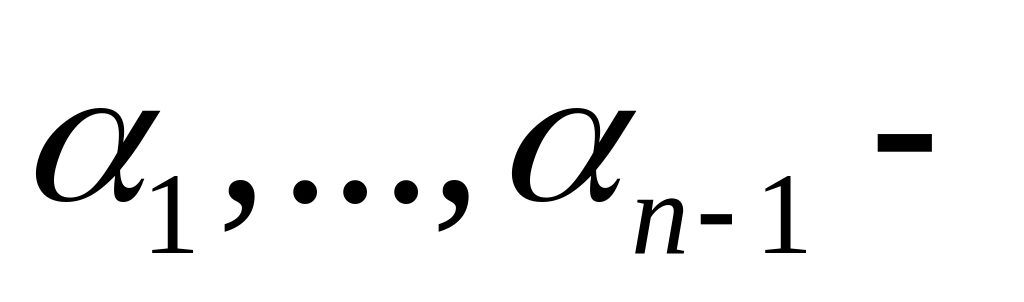базис подпространства .

9. Точка 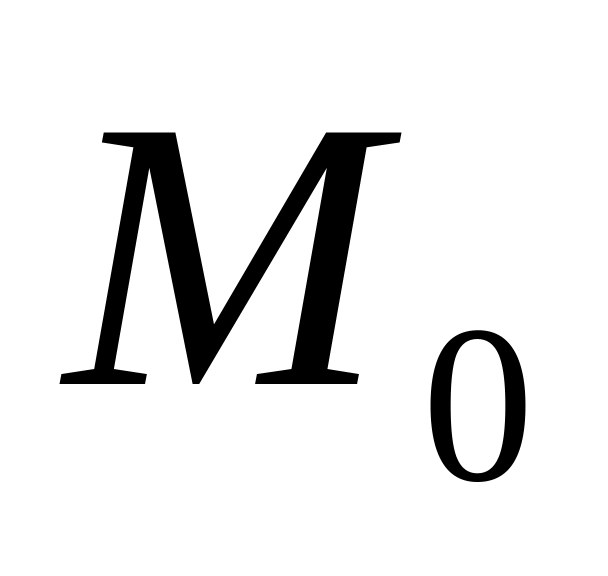принадлежит гиперплоскости , вектор перпендикулярен . Доказать, что 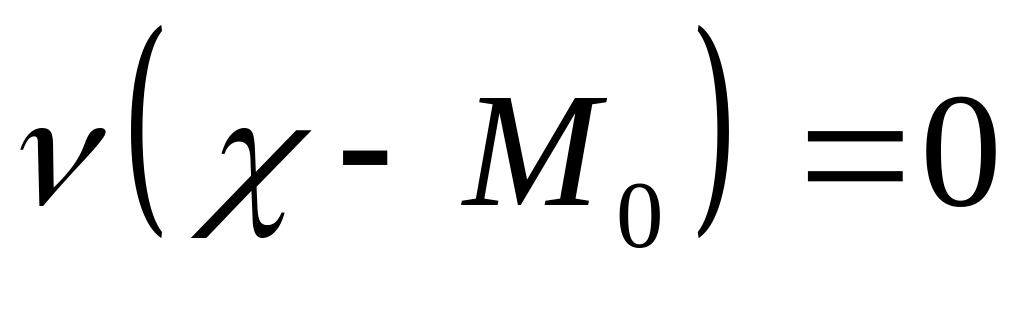– уравнение гиперплоскости .

10. Найти параметрическое уравнение гиперплоскости .

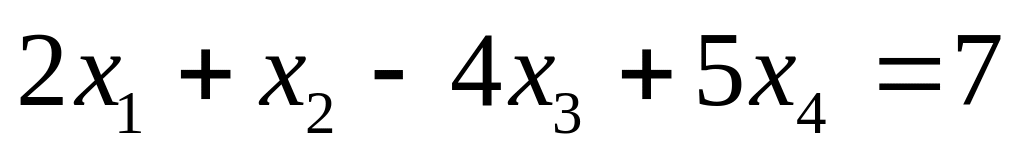11. Написать общее уравнение гиперплоскости, проходящей через точки .

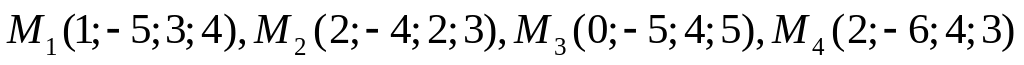3. Полупространства пространства

□ Теорема 2.22. Если точка N не принадлежит гиперплоскости , то прямая l, имеющая уравнение , пересекает гиперплоскость в единственной точке , которая называется проекцией точки N на гиперплоскость .

Доказательство. Чтобы найти точки пересечения прямой l и гиперплоскости , надо найти все решения системы уравнений

.

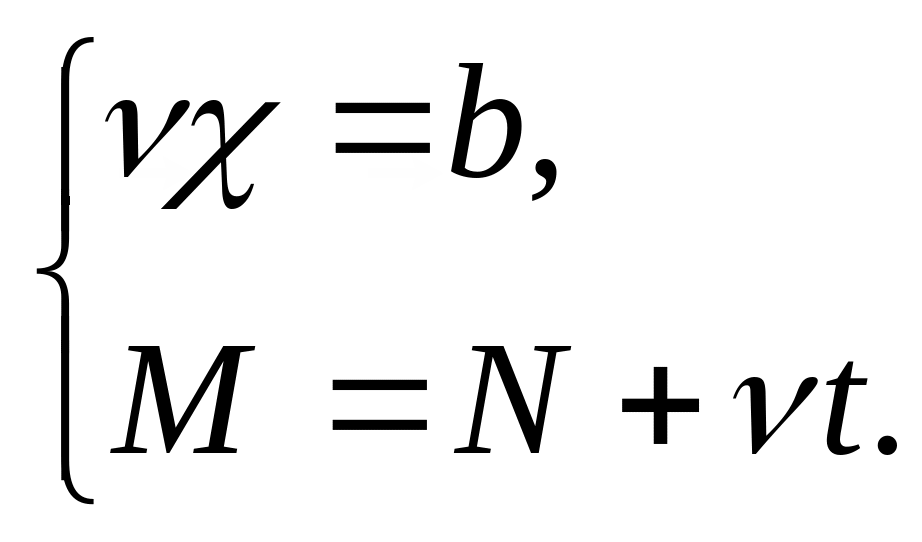Имеем

,

т. е. система уравнений имеет единственное решение. После подстановки найденного значения t в правую часть уравнения прямой l получим точку ■

• Следствие. Если проекция точки N на гиперплоскость , то вектор 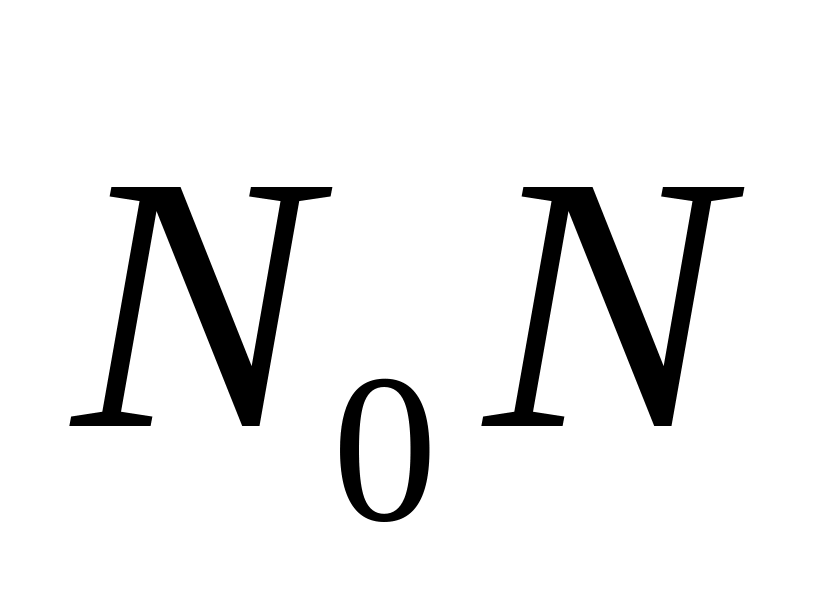коллинеарен нормальному вектору гиперплоскости .

Действительно, . Отсюда или и, значит, .

Пусть дана гиперплоскость и – нормальный вектор этой гиперплоскости. Все точки пространства , не принадлежащие гиперплоскости, разобьем на два множества и : полупространству принадлежат все точки М пространства , для которых векторы и одинаково (противоположно) направлены, где – проекция точки на гиперплоскость , т.е.

, .

Заметим, каждая точка пространства , не принадлежащая , попадает либо во множество , либо во множество . Действительно, если – проекция на гиперплоскость , то согласно следствию к теореме 2.27 векторы и коллинеарны. Следовательно, либо , либо , а поэтому или , или .

□ Теорема 2.23. Каждая гиперплоскость , заданная уравнением , разбивает пространство на два полупространства и , причем точки полупространства являются решениями неравенства

,

а точки полупространства – решениями неравенства

.

Доказательство. Пусть точка не принадлежит гиперплоскости , а – ее проекция на эту гиперплоскость. Тогда

(9)

Из условия (9) и равенства имеем:

. (10)

Используя равенство (10) и условия , получим:

,

.■

• Следствие. Расстояни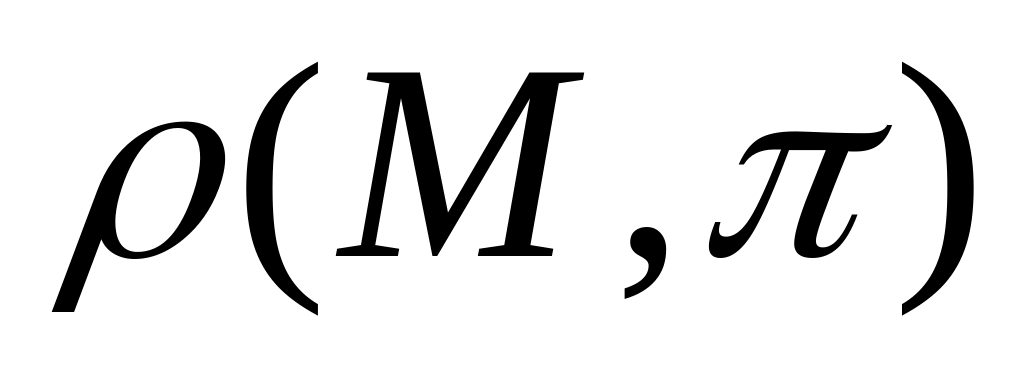е от точки до гиперплоскости , заданной уравнением находится по формуле:

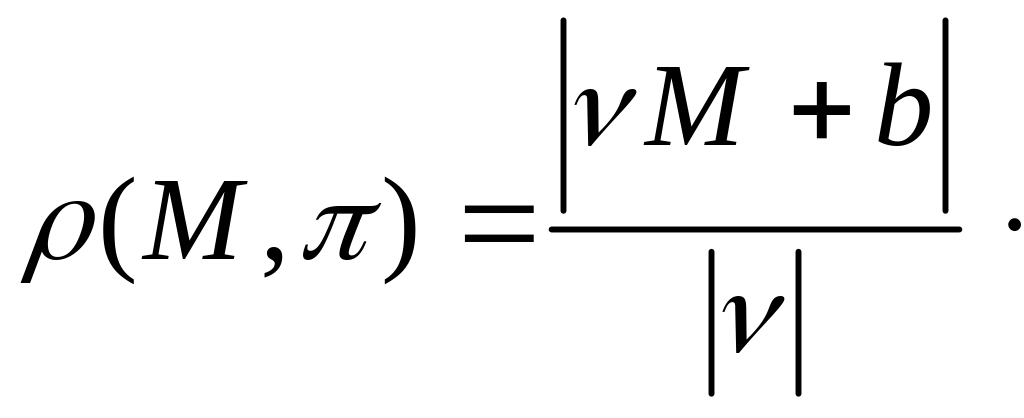
Доказательство. Из формулы (10) следует, что

.

Теперь из этого равенства, учитывая что

находим расстояние от точки до гиперплоскости :

●

Теорема 2.24. Дано уравнение гиперплоскости, которая разбивает пространство на два полупространства. Справедливы следующие утверждения:

1) Если точки и лежат в одном полупространстве, то отрезок находится в том же полупространстве.

2) Если точки и лежат в разных полупространствах, то отрезок имеет единственную общую точку с гиперплоскостью.

Доказательство.

1) Предположим, что точки и лежат в полупространстве , т.е.

(11)

(12)

Если − произвольная точка интервала , то она удовлетворяет условию . Умножим неравенство (11) на число , а неравенство (12) на число и сложим полученные неравенства:

,

т.е. произвольная точка интервала лежит в одном полупространстве с точками и .

Доказательство 1) утверждения в случае, когда точки и лежат в полупространстве , проводится аналогично.

2) Так как точки и лежат в разных полупространствах, то

, (13)

. (14)

Умножим неравенство (13) на число :

− (15)

и сложим неравенства (14) и (15)

(16)

Найдем точку пересечения прямой , c гиперплоскостью . Имеем

.

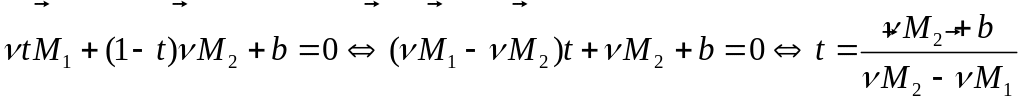Точка пресечения прямой с гиперплоскостью будет лежать на отрезке , если параметр принадлежит интервалу т.е. Из условий (14) и (16) следует, что . Докажем, что . Предположим противное. Тогда, ввиду неравенства (16), имеем

,

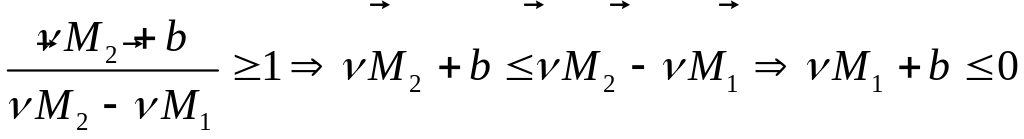что противоречит условию (13).■

Задачи

1. Доказать, что если аффинное множество не имеет общих точек с гиперплоскостью, то оно находится в одном полупространстве относительно гиперплоскости.

2. Написать уравнение аффинного множества размерности 3, расположенного в одном полупространстве относительно гиперплоскости .

3. Какова наибольшая размерность аффинного множества, которое может содержаться в одном полупространстве пространства ?

4. Дана гиперплоскость и аффинное множество . Доказать, что содержится в одном полупространстве относительно гиперплоскости тогда и только тогда, когда, во-первых, направляющее подпространство множества содержится в направляющем подпространстве гиперплоскости и, во-вторых, содержит точку, не принадлежащую