2.8.Прямые, плоскости и полупространства в

пространствах и

1. Параметрическое уравнение прямой в пространствах Т и

Т и плоскости в пространстве Т

1. □ Уравнение

= + t

является уравнением прямой в пространстве (или в пространстве ) тогда и только тогда, когда прямая проходит через точку М параллельно ненулевому вектору .

Доказательство следует из теоремы 2.17.■

Введем координаты точек , и вектора

Теперь параметрическое уравнение прямой в пространстве в координатной форме имеет вид:

Каждый ненулевой вектор, параллельный прямой, называется направляющим вектором этой прямой.

2.□ Уравнение

= + +

является уравнением плоскости в пространстве Т тогда и только тогда, когда плоскость проходит через точку параллельно двум неколлинеарным векторам и .

Доказательство следует из теоремы 2.21.■

Запишем параметрическое уравнение плоскости в координатной форме. Для этого введем координаты точек и векторов: Теперь параметрическое уравнение плоскости будет иметь вид:

○ Примеры

1. Написать уравнение прямой l, проходящей через точку М(−2;5) параллельно прямой :

Решение. Коэффициенты при параметре t в уравнении прямой являются координатами вектора , параллельного прямой и, значит, прямой l. Теперь параметрическое уравнение прямой l имеет вид:

2.Найти точку пересечения прямых

Решение. Пусть точка является пересечением прямых. Тогда ее координаты − решение уравнения каждой прямой

Итак, точка имеет координаты .

3. Даны вершины треугольника и . Составить параметрическое уравнение биссектрисы угла .

Решение. Биссектриса проходит через точку . Чтобы написать ее уравнение, достаточно найти координаты направляющего вектора биссектрисы. Вектор будем искать в виде: +

Коэффициенты и найдем из условия равенства косинусов углов между векторами и . Находим координаты векторов , а затем найдем скалярные произведения , , . Теперь имеем следующую цепочку импликаций:

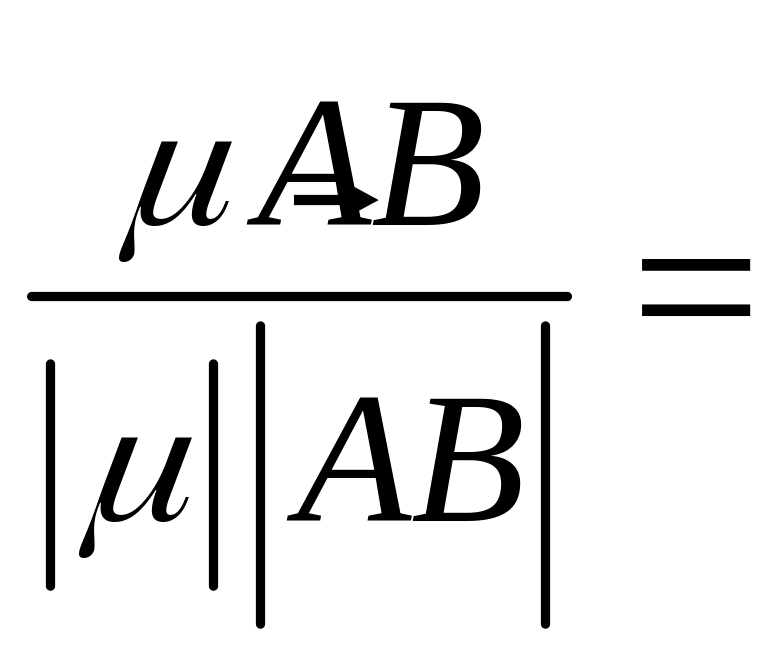
= − ) = 0 ( + )( − ) = 0 + ( − = 0

Полагая, получим координаты вектора . Параметрическое уравнение биссектрисы угла имеет вид:

4.Найти координаты точки которая симметрична точке (4;1;6) относительно прямой, проходящей через точки (−3;5;1) и (1;1;3).

Решение. Прямая проходит через точки и . Ее направляющий вектор коллинеарен вектору = (4;−4;2). Тогда направляющий вектор прямой . Теперь параметрическое уравнение прямой будет иметь вид:

Пусть координаты точки Точка − середина

отрезка и, значит, принадлежит прямой . Отсюда следует, что ее координаты являются решениями уравнения прямой :

Так как точки и симметричны относительно прямой, то вектор перпендикулярен прямой . Отсюда вытекает следующая цепочка импликаций:

прямой

Итак, координаты точки :

5.Доказать, что в пространстве прямые

: = + и : = + лежат в одной плоскости тогда и только тогда, когда , , = 0.

Решение вытекает из следующей цепочки равносильных утверждений:

прямые и лежат в плоскости векторы , , отложенные от точки лежат в плоскости векторы , , линейно зависимы

6.Написать параметрическое уравнение плоскости, проходящей через точки (2;−1;2) и (1;0;1) параллельно прямой

Решение. Чтобы написать параметрическое уравнение плоскости надо знать координаты точки, принадлежащей плоскости, и координаты пары неколлинеарных векторов, параллельных плоскости.

В качестве точки, принадлежащей плоскости можно взять любую из точек . Так как эти точки принадлежат плоскости, то вектор параллелен плоскости, т.е. вектор = =(−1;1;−1) параллелен плоскости. Вектор параллелен данной прямой и, значит, параллелен искомой плоскости. Векторы и – неколлинеарные векторы, так как координаты этих векторов не пропорциональны. Теперь параметрическое уравнение плоскости в векторной форме имеет вид:

= + + ,

или в координатной форме

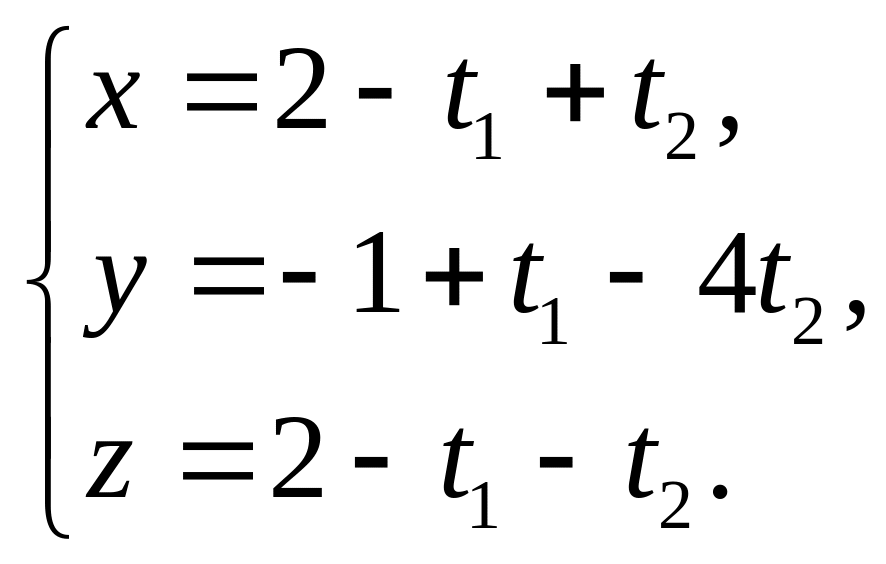
7.Написать уравнение плоскости, в которой лежит каждая прямая

: :

Решение. Выясним сначала, лежат ли прямые и в одной плоскости. Прямая проходит через точку (−2;0;1) параллельно вектору = (2;−3;4), а прямая проходит через точку (3;1;7) параллельно вектору = (3;4;2). Из задачи 5 следует, что прямые и лежат в одной плоскости тогда и только тогда, когда . Так как = (5;1;1), то

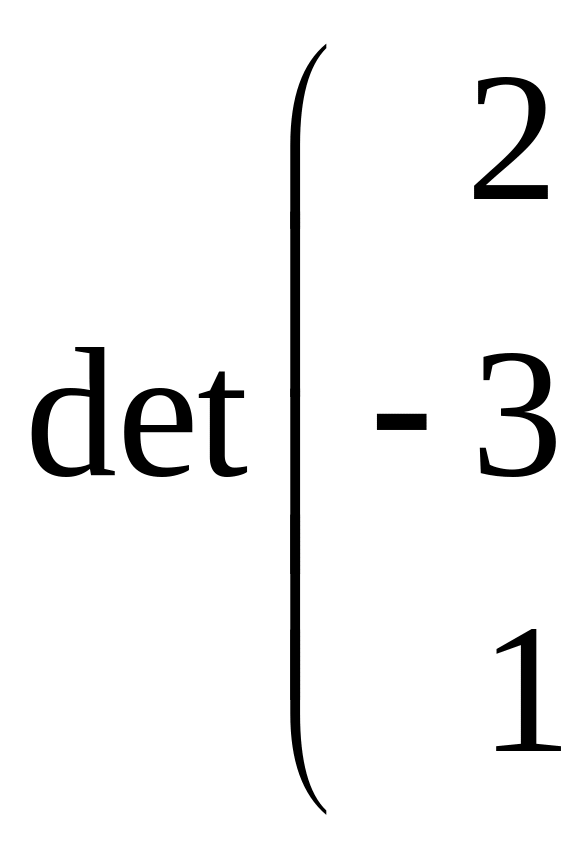
= 0.

Итак, прямые и лежат в одной плоскости.

Напишем параметрическое уравнение плоскости , которая проходит через прямые и . Точка принадлежит плоскости , а векторы и параллельны плоскости и линейно независимые. Искомое уравнение плоскости имеет вид

8. Написать параметрическое уравнение прямой , перпендикулярной каждой из двух прямых

: :

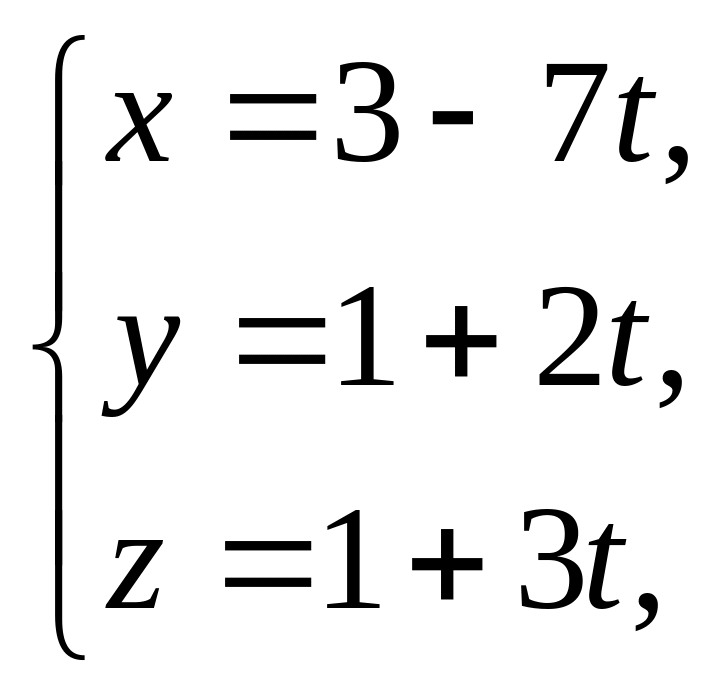
и пересекающей каждую из прямых .

Решение. Вектор = (1;2;−1) параллелен прямой , а вектор =(−7;2;3) − прямой . Обозначим через направляющий вектор искомой прямой l. По условию прямая l перпендикулярна и прямой , и прямой . Отсюда вытекает

Полагаем координату = 1, а затем найдем значения координат и : =2, . Следовательно, вектор имеет координаты: . Параметрическое уравнение прямой l имеет вид

где координаты точки, принадлежащей прямой l. В условии дано, что прямая l должна пересекать прямые и . Отсюда следует, что прямые l и , а также прямые l и лежат в одной плоскости. Теперь, используя задачу 5, имеем

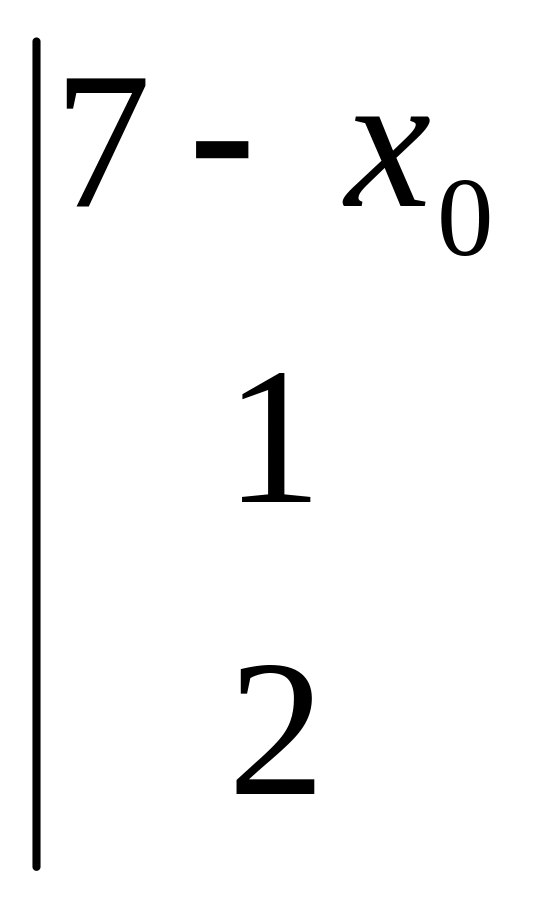
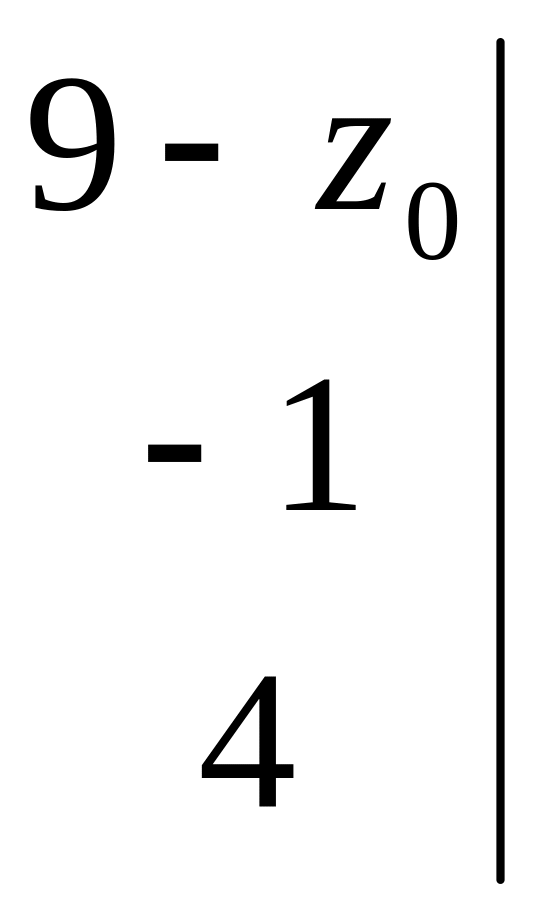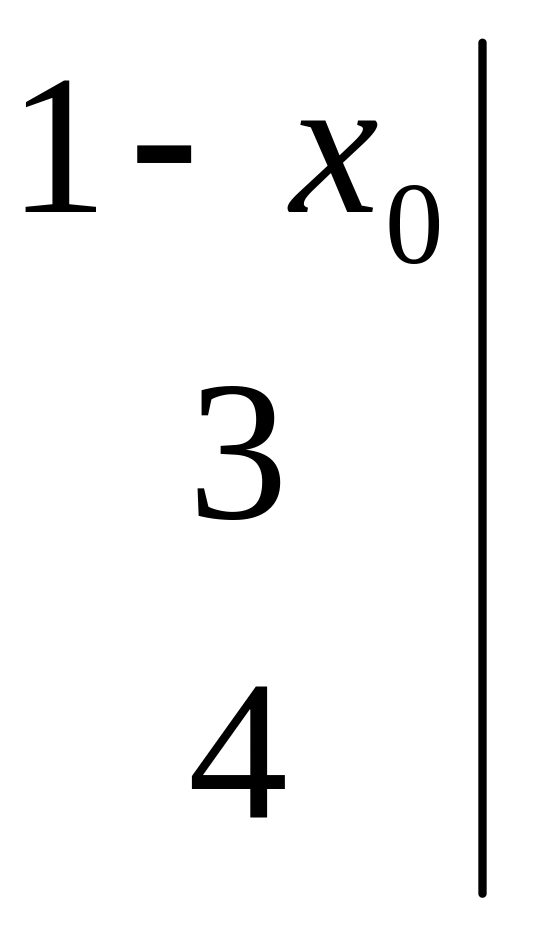= 0, = 0.

Вычислим определители и после упрощений получим систему уравнений

Полагая в этой системе найдем значения координат и : = 1, . Параметрическое уравнение прямой l имеет вид

●

Задачи

1.Выяснить, принадлежат ли прямой

точки (2;−5) и (3;1).

2.Даны точки (0;4) и (3;−1). Написать параметрическое уравнение прямой, проходящей через точку (1;2) параллельно прямой MN.

3. Найти точку пересечения прямых и :

4.Найти проекцию точки (−2;−9) на прямую, проходящую через точки M(0;19) и N(−1;8).

5. Составить параметрическое уравнение прямой, равноудаленной от параллельных прямых

6. Написать параметрическое уравнение прямых, которые делят пополам углы, образованные двумя пересекающимися прямыми

а) b)

7. Составить параметрическое уравнение прямой, проходящей через точку (2;−5;3) перпендикулярно прямой

и пересекающей ее.

8. Найти точку пересечения прямых

9. Написать параметрическое уравнение плоскости, которая проходит через точку ( параллельно плоскости

10. Составить параметрическое уравнение плоскости, которая проходит через точки и параллельно прямой

11. Известны координаты вершин тетраэдра: А(0;0;2), B(3;0;5), C(1;1;0) и D(4;1;2). Найти параметрические уравнения его граней.

12.Написать параметрическое уравнение плоскости, которая проходит через две параллельные прямые

13.Составить параметрическое уравнение плоскости, которая проходит через точку и прямую