
- •Глава II. Аффинные множества
- •2.2. Аффинные множества
- •2.3. Задание аффинных множеств
- •1. Задание аффинного множества системой линейных уравнений
- •3. Задание аффинного множества
- •2.4. Направляющее подпространство
- •□ Теорема 2.7. Если – аффинное множество в пространстве , то множество является подпространством пространства .
- •1. Направляющее подпространство множества
- •2. Направляющее подпространство аффинной оболочки
- •3. Направляющее подпространство
- •2.5. Размерность аффинного множества
- •2.6. Уравнения аффинного множества
- •1. Уравнение фигуры
- •2. Параметрическое уравнение аффинного множества
- •2. Общее уравнение аффинного множества в пространстве
- •2.7. Прямые гиперплоскости и полупространства
- •1. Прямые в пространстве
- •2. Гиперплоскости в пространстве
- •3. Полупространства пространства
- •2.8.Прямые, плоскости и полупространства в
- •2. Общее уравнение прямой в пространствах и
- •3. Полупространства в пространствах и
2. Общее уравнение аффинного множества в пространстве
□Теорема 2.16. Дано аффинное множество размерности . Тогда справедливо следующее утверждение. Система уравнений
![]() (5)
(5)
является
уравнением аффинного множества
тогда и только тогда, когда множество
проходит через точку
перпендикулярно линейно независимым
векторам
![]() .
.
Необходимость. Дано, что система уравнений (5) уравнение аффинного множества , т.е. множество является множеством решений системы (5).
Так
как после подстановки точки
в систему (5) вместо вектора
![]() получим верные числовые равенства, то
точка
получим верные числовые равенства, то
точка
![]() решение системы уравнений (5) и, значит,
.
решение системы уравнений (5) и, значит,
.
Докажем, что векторы линейно независимые и перпендикулярны аффинному множеству . Направляющее подпространство задается системой уравнений (теорема 2.10)
![]()
![]()
Теперь
из теоремы 1.24 вытекает, что подпространство
![]() .
По условию,
.
По условию,
![]() .
Следовательно,
.
Следовательно,
![]() (теорема
1.23). Отсюда векторы
образуют базис подпространства
(теорема
1.23). Отсюда векторы
образуют базис подпространства
![]() (теорема 1.8) и, значит, линейно независимы
и перпендикулярны аффинному множеству
.
(теорема 1.8) и, значит, линейно независимы
и перпендикулярны аффинному множеству
.
Достаточность.
Дано,
аффинное множество
проходит через точку
перпендикулярно линейно независимым
векторам
.
Надо доказать, что
множество
решений системы уравнений (5). Обозначим
![]() множество
решений системы уравнений (5) и докажем,
что
множество
решений системы уравнений (5) и докажем,
что
![]() .
Для этого установим, что
общая точка множеств
и
,
и направляющие подпространства этих
аффинных множеств совпадают.
.
Для этого установим, что
общая точка множеств
и
,
и направляющие подпространства этих
аффинных множеств совпадают.
Точка
является решением системы уравнений
(5) и, значит,
.
Векторы
перпендикулярны множеству
,
а поэтому принадлежат подпространству
.
Так как
![]()
![]() и
векторы
линейно независимы, то система векторов
образует базис подпространства
(теорема 1.8) и, значит,
.
Теперь из теорем 1.22 и 1.23 следует
и
векторы
линейно независимы, то система векторов
образует базис подпространства
(теорема 1.8) и, значит,
.
Теперь из теорем 1.22 и 1.23 следует
![]()
Далее, из теоремы 2.10 вытекает
![]()
Итак, направляющие подпространства аффинных множеств и совпадают. Из теоремы 2.14 вытекает совпадение множеств и .■
Система уравнений (5), где линейно независимые векторы, называется общим уравнением аффинного множества размерности .
◊Замечание. В общем уравнении аффинного множества размерности линейно независимые векторы образуют базис подпространства .
Действительно,
так как
![]() ,
то из теоремы 1.8 следует, что
,
то из теоремы 1.8 следует, что
![]() базис
подпространства
.♦
базис
подпространства
.♦
Приведем алгоритм построения общего решения аффинного множества .
1.Задать аффинное множество .
2.Найти точку и базис подпространства .
3.Написать общее уравнение аффинного множества :
![]()
Пример
Аффинное множество задано параметрическим уравнением:
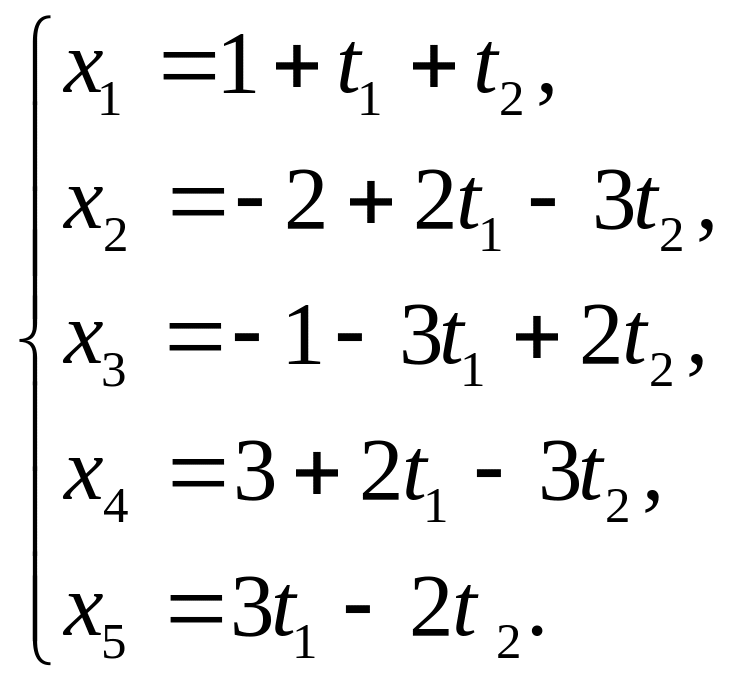
Напишите
общее уравнение множества
![]() .
.
Решение. Чтобы написать общее уравнение множества достаточно знать координаты точки, принадлежащей , и базис подпространства . Запишем параметрическое уравнение в векторной форме
,
где
точка
![]() принадлежит
и векторы
принадлежит
и векторы
![]() ,
,![]() базис направляющего подпространства
.
Следовательно, подпространство
базис направляющего подпространства
.
Следовательно, подпространство
![]() задается системой уравнений
задается системой уравнений
![]()
Векторы
![]() ,
,
![]() ,
,
![]()
образуют фундаментальный набор решений однородной системы уравнений, т.е. образуют базис подпространства . Теперь система уравнений
![]() (6)
(6)
является общим уравнением множества . Так как
![]() ,
,![]() ,
,![]()
то система уравнений (6) в координатной форме имеет вид
![]() ●
●
Задачи
1.
Если
![]() уравнение
аффинного множество
,
то
общим уравнением этого множества
является общее решение
уравнение
аффинного множество
,
то
общим уравнением этого множества
является общее решение
![]() системы линейных уравнений
системы линейных уравнений![]() полученное методом Гаусса.
полученное методом Гаусса.
2.
Напишите общее уравнение аффинного
множества
,
которое содержит точку
![]() (1,2,−1,−2.1)
и направляющее подпространство
(1,2,−1,−2.1)
и направляющее подпространство
![]() которого совпадает с множеством решений
системы уравнений
которого совпадает с множеством решений
системы уравнений
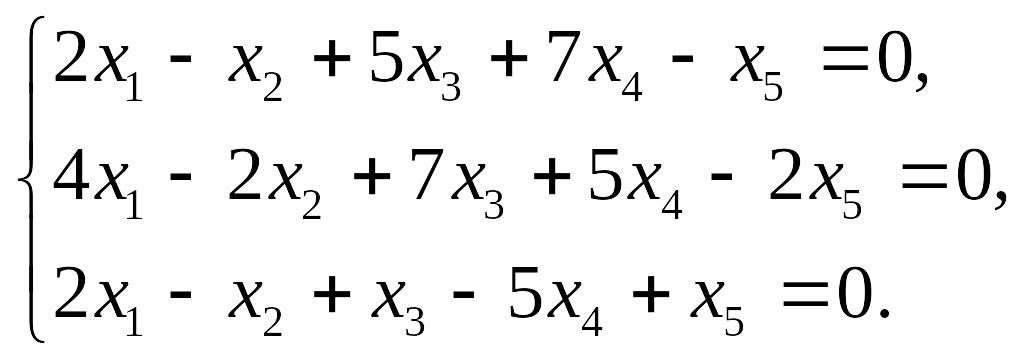
3.Дано
аффинное множество
![]() ,
где
,
где
![]() (2,1,2,1),
(2,1,2,1),
![]() =(1,1,−1,1)
,
=(1,1,−1,1)
,
![]() =(2,1,−1,3),
=(2,1,−1,3),
![]() =(0,−1,1,1).
=(0,−1,1,1).
Напишите общее уравнение множества .
4.
Аффинное множество
![]() задано системой уравнений
задано системой уравнений
![]() .
.
Напишите
общее уравнение аффинного множества
![]() ,
которое содержит множество
,
имеет размерность четыре и
,
которое содержит множество
,
имеет размерность четыре и
а) содержит точку (2,-5,3,1,4);
б)
вектор
![]() параллелен множеству
.
параллелен множеству
.
