2.2. Аффинные множества
Подмножество
пространства
называется аффинным,
если для
каждой пары
точек
из множества
выполняется условие: множеству
принадлежат все
точки
М пространства
,
для которых
(1)
◊ Замечание.
Если в равенстве (1) положить,
то из условия
следует
.
Теперь в определении аффинного множества
вместо (1) можно написать
♦
□ Tеорема2.3. Для каждого множества из пространства равносильны следующие утверждения:
– аффинное множество;
для каждых двух точек из множества конец вектора
,
отложенный от точки
,
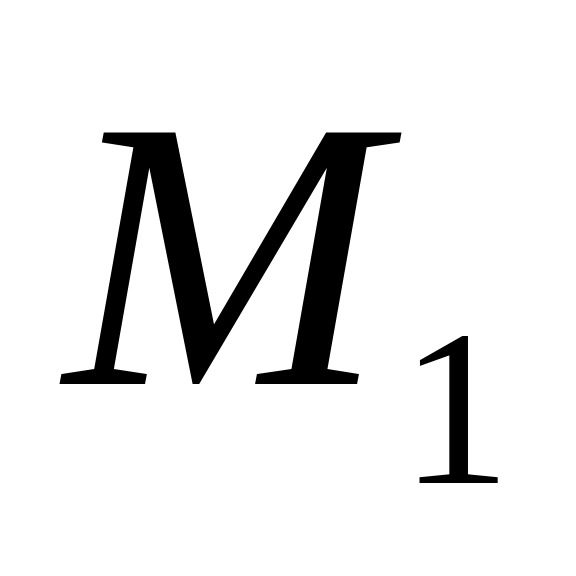принадлежит
при любом
,
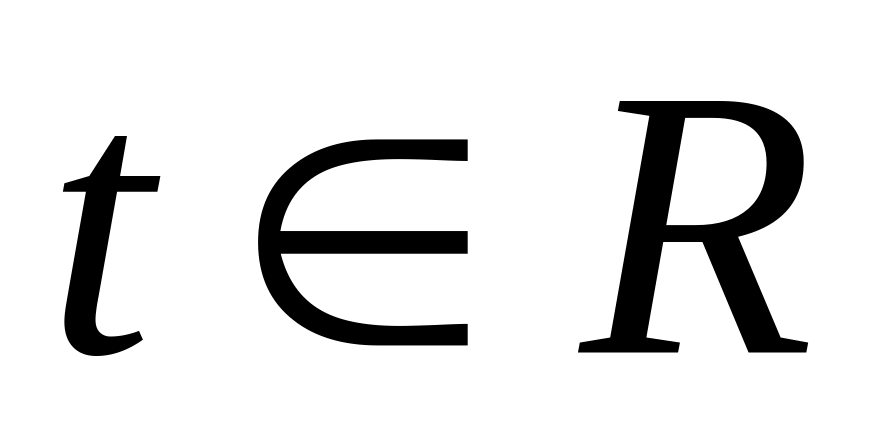т.е.
,
=
.
Доказательство.
1)
2)
Дано, что
– аффинное множество,
=
,
точки
принадлежат
множеству
.
Требуется доказать: M
.
Это утверждение вытекает из определения
аффинного множества и следующей цепочки
импликаций:
=
=
(1− t)
+ t
.
2)
1)
Докажем что,
– аффинное множество. Для этого надо
установить, что из условий
,
вытекает
.
Используя условие 2), имеем следующую
цепочку импликаций:
−
=
(
−
)
=
■
○ Примеры
1.
Множество
,
состоящее из одной точки
,
является аффинным множеством.
Так
как конец вектора
,
отложенного от точки
,
совпадает с точкой
и, значит, принадлежит
.
2.
Прямые в пространствах
и
являются аффинными множествами.
Пусть
произвольная прямая и
– любые ее две точки. Обозначим через
конец вектора
,
отложенного от точки
,
т.е.
=
.
Отсюда следует коллинеарность векторов
и
.
Так как начала этих векторов совпадают,
то точки
и
лежат на одной прямой и, значит,
Теперь из теоремы 2.3 следует, что
– аффинное множество
3. Плоскости в пространстве являются аффинными множествами.
Пусть
произвольная плоскость и
– любые ее две точки. Рассмотрим прямую
проходящую через точки
.
Прямая
принадлежит плоскости
.
Обозначим через
конец вектора
,
отложенного от точки
т.е.
.
Так как
аффинное множество, то
Прямая
принадлежит плоскости
и, значит,
.
Теперь из теоремы 2.3 следует, что
–
аффинное множество.
4. Множество , совпадающее со всем пространством , очевидно, является аффинным множеством.●
При изучении аффинных множеств будет полезна нижеследующая лемма.
Лемма.
Точки
принадлежат
аффинному множеству
.
Если для точки
выполняется равенство
то точка М принадлежит множеству .
Доказательство. Имеем следующую цепочку импликаций
где
.
В
этом равенстве точки
принадлежат множеству
и сумма коэффициентов равна 1, из
определения аффинного множества
следует
.
Теперь из равенства
,
.
и определения аффинного множества следует М .■
Задачи
1.Доказать, что пересечение аффинных множеств будет аффинным множеством.
2. Доказать, что аффинное множество, содержащее две различные точки, содержит бесконечно много различных точек.
3.
Дано аффинное множество
в пространстве
и матрица
порядка n.
Доказать, что множество
,
состоящее
из всех точек
пространства
для
которых
является
аффинным множеством.
4.Дано множество в пространстве . Доказать равносильность утверждений:
а) – аффинное множество;
б)
для каждых двух различных точек
,
из
множества
прямая
принадлежит множеству
.
5. Дано аффинное множество в . Доказать, что
а)
если множество
содержит различные точки
и
,
то
содержит прямую, проходящую через эти
точки;
б)
если множество
содержит прямую
и точку
не принадлежащую
,
то
содержит плоскость, проходящую через
точку
и прямую
;
в) если содержит плоскость и точку, не принадлежащую этой плоскости, то совпадает с пространством .
6. Доказать, что каждое аффинное множество в пространстве совпадает с одним из следующих множеств: точка, прямая, плоскость и пространство .