1.2. Подпространства

Подмножество пространства называется подпространством, если оно обладает следующими двумя свойствами:

1. Для каждой пары векторов подпространства сумма принадлежит .

2. Для каждого вектора из подпространства и любого действительного числа вектор принадлежит .

Примеры

1. Множество L={ }, состоящее из одного нулевого вектора , является подпространством.

Действительно, и .

2. Пространство является подпространством, так как сумма n-мерных векторов и произведение n-мерного вектора на число являются n-мерными векторами.

3. Линейная оболочка является подпространством.

Утверждение вытекает из свойств линейной оболочки.

4. Множество всех решений однородной системы линейных уравне-ний с n неизвестными является подпространством, которое будем обозначать символом

Утверждение вытекает из свойств решений однородной системы линейных уравнений.

□ Теорема 1.2. Если каждый вектор системы принадлежит подпространству L и вектор разлагается по системе векторов , то вектор принадлежит подпространству L.

Доказательство этого утверждения проведем методом математической индукции по числу векторов в системе.

Если то и из условия 2 определения подпространства следует, что Предположим, что теорема справедлива, если , т. е. каждый вектор, который разлагается по системе векторов , принадлежит подпространству L, и пусть

Перепишем это равенство в виде где . Из индуктивного предположения следует, что вектор . Так как вектор L, то и, значит, + . Этим установлено, что вектор ■

Следствие. Если каждый вектор системы принадлежит подпространству , то линейная оболочка содержится в подпространстве .

Доказательство. Пусть вектор . Тогда g разлагается по системе векторов . Теперь из теоремы 1.2 следует, что

Пример

Выяснить, принадлежит ли линейная оболочка системы векторов

, , ,

подпространству решений системы линейных уравнений

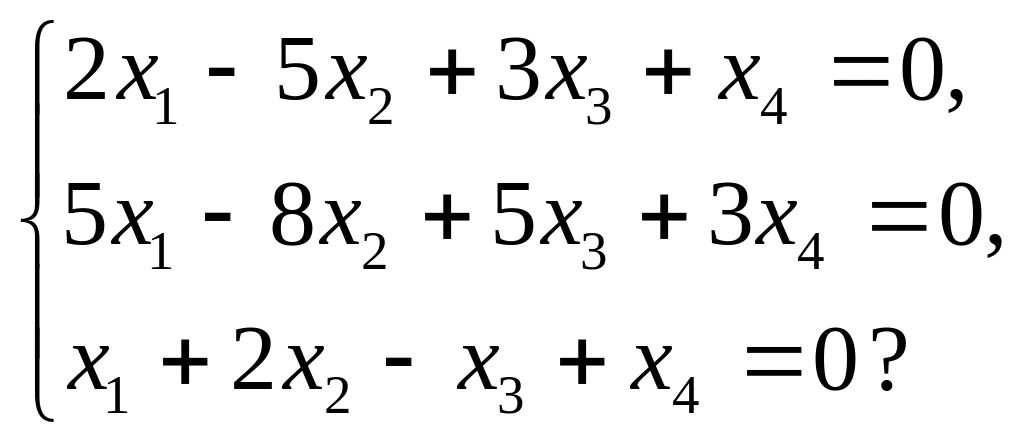
Решение. Вначале необходимо выяснить, являются ли векторы решениями системы линейных уравнений. Подстановка координат этих векторов в систему уравнений вместо неизвестных приводит к верным числовым равенствам. Это означает, что векторы являются решениями системы уравнений и, значит, принадлежат подпространству решений этой системы. Теперь из следствия к теореме 1.2 вытекает, что линейная оболочка содержится в подпространстве решений системы линейных уравнений.

Задачи

1. Доказать, что каждое подпространство содержит нулевой вектор.

2. Дано подпространство . Доказать, что если , то .

Выяснить, является ли подпространством пространства R каждое из следующих множеств (начало каждого вектора предполагается совпадающим с началом координат).

3. Все векторы, каждый из которых лежит хотя бы в одной из координатных плоскостей .

4. Все векторы, концы которых лежат на данной прямой.

5. Все векторы, концы которых не принадлежат данной прямой.

6. Все векторы, у которых все координаты положительны.

Выяснить, является ли подпространством пространства каждое из следующих множеств.

7. Все векторы, координаты которых – целые числа.

8. Все векторы, сумма координат которых равна нулю.

9. Все векторы, сумма координат которых не равна нулю.

10. Все линейные комбинации данной системы векторов.

11. Множество всех векторов, которое обладает свойством

или ,

где и фиксированные квадратные матрицы порядка n.