Базисы линейной оболочки

□ Теорема 1.6. Пусть линейная оболочка системы , содержащей ненулевой вектор. Тогда справедливы следующие утверждения:

1. Базис системы векторов является базисом линейной оболочки L.

2. Линейная оболочка L имеет такой базис, который не является базисом системы векторов .

Доказательство

1. Так как система содержит ненулевой вектор, то она обладает базисом . Докажем, что – базис линейной оболочки. Система векторов линейно независима. Следовательно, достаточно показать, что каждый вектор из подпространства разлагается по векторам . Так как вектор , то вектор разлагается по системе векторов . Отсюда и из того, что каждый из векторов разлагается по векторам , вытекает, что разлагается по системе векторов (§ 1, утверждение 5[1]).

2. Множество содержит бесконечно много различных ненулевых векторов. Действительно, если , то 2 ,3 ,.., n – различные векторы множества . Следовательно, в этом множестве найдется такой ненулевой вектор , что , i=1,2,..,m. Дополняя вектор до базиса , получим базис, который не является частью и, значит, не может быть базисом системы векторов .■

Базисы подпространства решений однородной системы линейных уравнений

□ Теорема 1.7. Система векторов является базисом подпространства тогда и только тогда, когда – фундаментальный набор решений (ФНР) системы уравнений с n неизвестными.

Необходимость. Пусть система векторов базис подпространства L, а – какой-нибудь ФНР (теорема 5.7 [1]), n – число неизвестных в системе, r – ранг матрицы . Рассмотрим систему векторов

, .

Части и являются базисами этой системы векторов. Так как различные базисы системы векторов содержат одно и то же число векторов, то (теорема 2.15 [1]). Отсюда и из линейной независимости системы вытекает, что эти векторы образуют ФНР.

Достаточность. Если ФНР системы уравнений то векторы линейно независимы и каждое решение системы уравнений разлагается по векторам (теорема 5.8 [1]). Следовательно, − базис подпространства L. ■

Пример

Доказать, что множество всех n-мерных векторов, у которых сумма четных координат равна сумме нечетных, образует подпространство; найти базис этого подпространства.

Решение. Если векторы и принадлежат множеству то

Так как

то векторы и принадлежат множеству и, значит, подпространство.

Найдем базис подпространства . Из определения подпространства следует, что вектор принадлежит тогда и только тогда, когда его координаты являются решением уравнения

если у вектора число координат четно, и решением уравнения

если у вектора число координат нечетно.

Базисом подпространства является ФНР этих уравнений. Найдем ФНР первого уравнения, которое перепишем в виде

.

Табличная форма записи этого уравнения имеет следующий вид:

Базисом системы векторов является вектор , а разложения остальных векторов по базису имеют вид

.

Перепишем эти разложения в виде разложения вектора по системе векторов

,

,

,

……………………………………………..

,

.

Система векторов

(1, 1, 0, 0, …, 0, 0),

(1, 0, –1, 0, …, 0, 0),

(1, 0, 0, 1, …, 0, 0),

……………………..

(1, 0, 0, 0, …, –1 ,0),

(1, 0, 0, 0, … , 0, 1)

фундаментальный набор решений первого уравнения. Аналогично находится базис подпространства в другом случае.

Задачи

1. Доказать, что каждое ненулевое подпространство обладает бесконечным числом различных базисов.

2. Построить два различных базиса следующих подпространств:

а) L= ;

б) где =(1, 1, −1), =(1, −1, 1), = (−1, 1, 2);

в) где

3. Показать, что в пространстве для каждого имеется подпространство L, базис которого содержит ровно k векторов.

4. Даны подпространства и , причем содержится в . Векторы образуют базис подпространства и каждый вектор этой системы принадлежит подпространству . Доказать, что базис подпространства .

5. Даны подпространства и , причем содержится в и . Построить такой базис подпространства , чтобы все векторы этого базиса, принадлежащие , образовывали базис .

6. Даны подпространства и , причем содержится в и . Построить такой базис подпространства , каждый вектор которого не лежит в .

Доказать, что следующие множества векторов образуют подпространства и найти их базис и размерность:

7. Все n-мерные векторы, у которых нечетные координаты равны между собой.

8. Все n-мерные векторы вида (a, b, c, a, b, c, a, b, c,...), где a, b и c – любые действительные числа.

9. Все n-мерные векторы, у которых первая и последняя координаты равны между собой.

10. Все n-мерные векторы, у которых одни и те же координат равны нулю.

11. Все векторы вида где

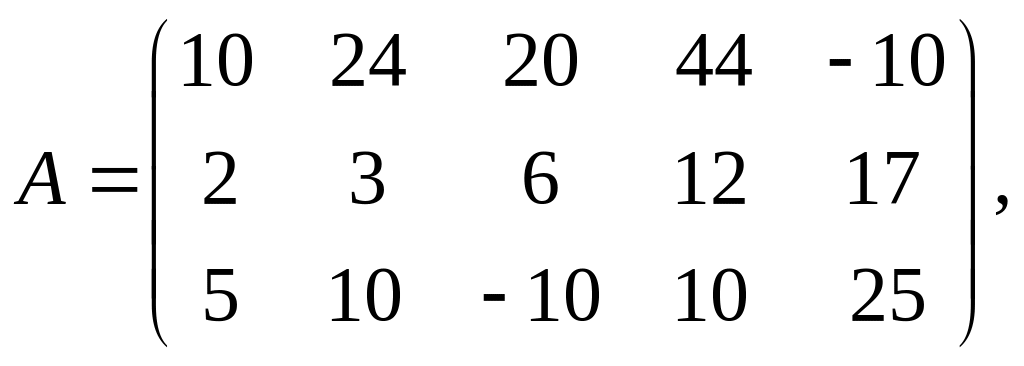
произвольный пятимерный вектор.