1.7. Ортогональное дополнение
Вектор
ортогонален
подпространству
тогда и только тогда, когда он ортогонален
каждому вектору из подпространства
.
В этом случае будем писать
.
□ Теорема
1.20. Вектор
ортогонален линейной оболочке
тогда и только тогда, когда он ортогонален
каждому вектору системы
.
Необходимость.
Если
,
то вектор
ортогонален каждому вектору подпространства
и, в частности,
ортогонален вектору
.
Достаточность.
Дано, что
.
Пусть
произвольный вектор из линейной оболочки
.
Тогда
.
Теперь найдем скалярное произведение
векторов
.
Отсюда следует, что вектор
ортогонален подпространству L.
■
Следствие. Вектор ортогонален подпространству тогда и только тогда, когда он ортогонален каждому вектору базиса подпространства . Действительно, каждое подпространство является линейной оболочкой своего базиса (теорема 1.10).
Пусть
– подпространство пространства
.
Обозначим символом
множество всех векторов пространства
,
которые ортогональны
,
т. е.
.
Множество называется ортогональным дополнением подпространства .
Теорема 1.21. Ортогональное дополнение подпространства является подпространством.
Доказательство.
Пусть
и
произвольный вектор из подпространства
L.
Тогда
и
.
Отсюда
,
(24)
.
(25)
Из
равенств (24) и (25) вытекает, что векторы
и
ортогональны подпространству
,
т. е.
и
.
■
Теоремы
1.22 и 1.24 будут посвящены заданию
подпространства
.
□ Теорема 1.22. Ортогональное дополнение подпространства совпадает с множеством решений системы линейных уравнений
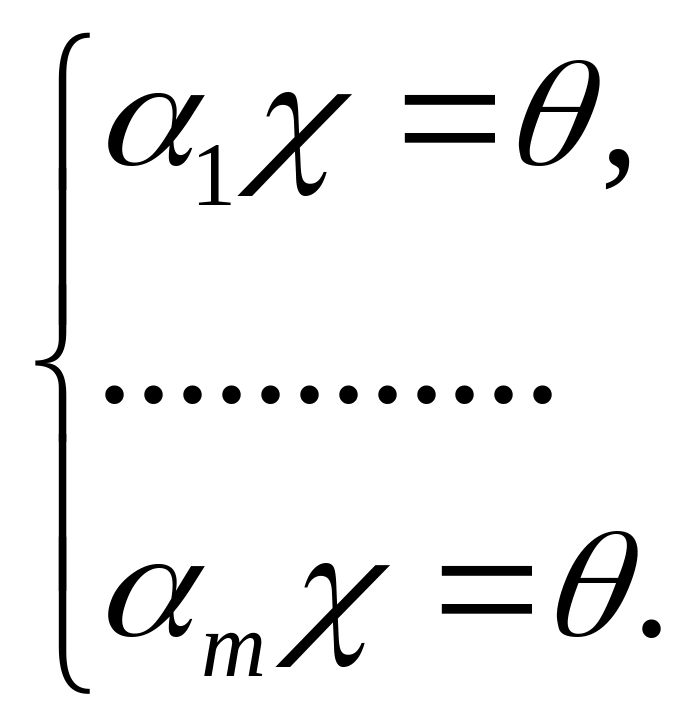(26)
Доказательство. Обозначим подпространство решений системы уравнений (26) и докажем совпадение подпространств и . Имеем следующую цепочку равносильных утверждений:
решение
системы уравнений (26)
Итак,
,
т. е.
.
■
В следующей теореме приведены основные свойства ортогонального дополнения подпространства.
□ Теорема 1.23. Пусть – подпространство пространства . Тогда справедливы следующие утверждения:
1.
2.
.
3.
.
Доказательство
1.
Пусть
базис
подпространства L.
Тогда
и
.
Теперь из теоремы 1.22 имеем
.
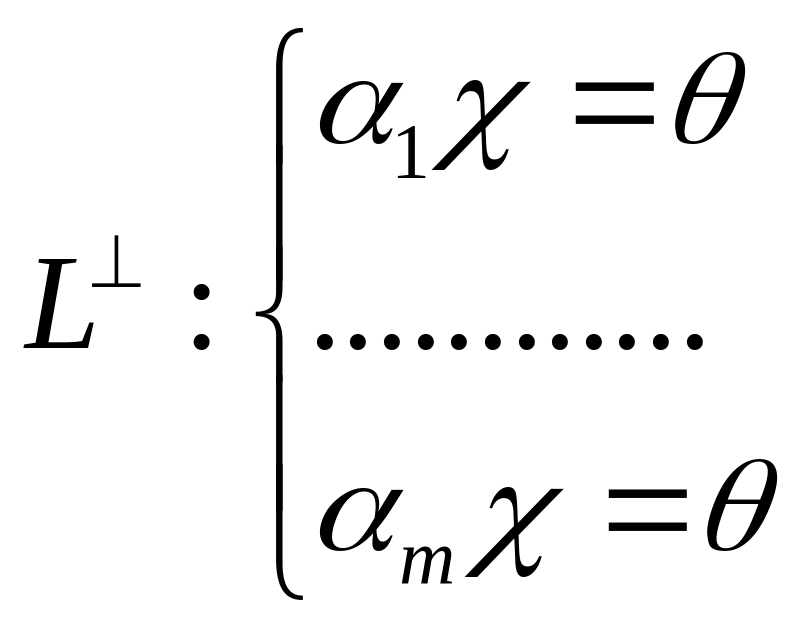(27)
Отсюда
.
Итак,
.
2.
Покажем сначала, что
.
Если
,
то
и
.
Отсюда
и, значит,
.
Теперь
установим, что
.
Ясно, что
и, значит, достаточно показать, что
(теорема 1.19). Имеем следующую цепочку
равенств:
.
3. Пусть – базис подпространства . Тогда и
.
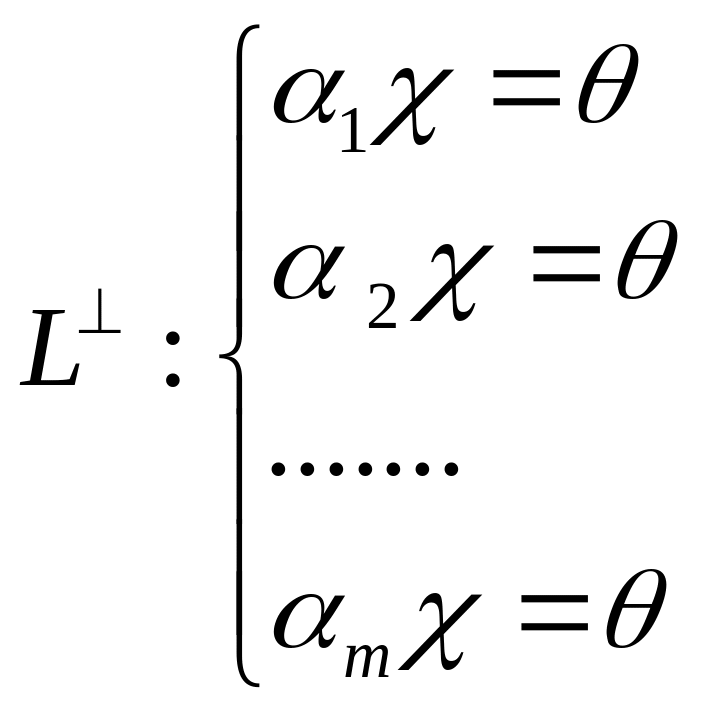(28)
Обозначим
через
фундаментальный набор решений системы
уравнений (28). Так как
базис подпространства
,
то
.
Теперь из теоремы 1.22 получаем, что
.
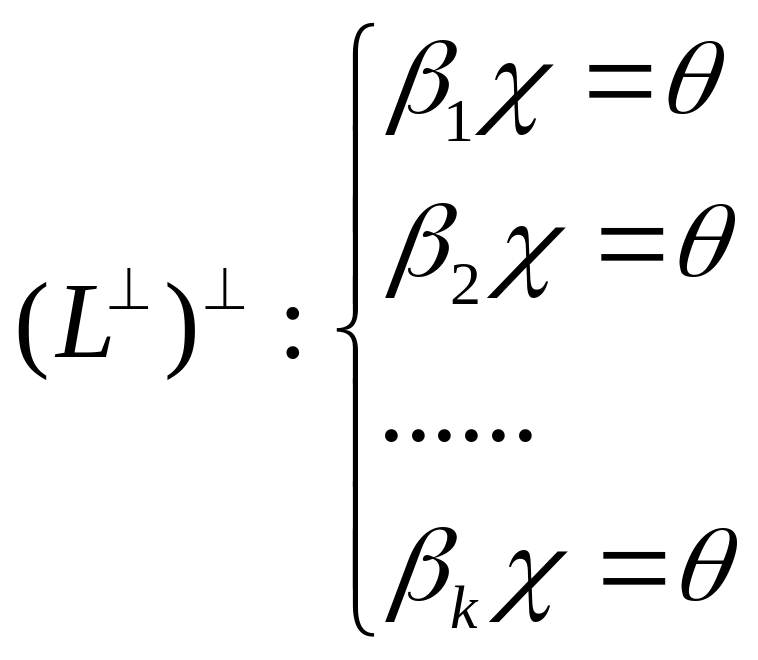(29)
С другой стороны, из теоремы 1.11 следует, что
.
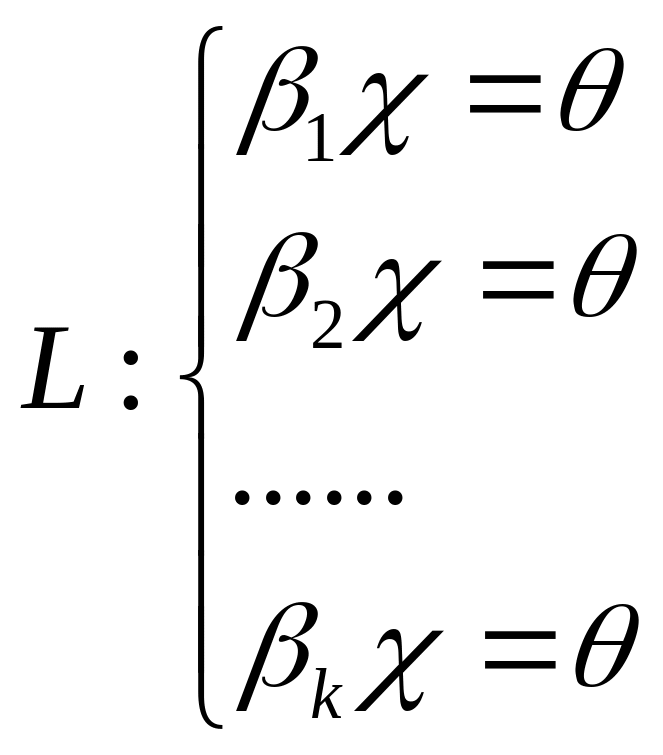(30)
Из соотношений (29) и (30) вытекает, что L = ( )^. ■
Cформулируем
и докажем еще одну теорему, посвященную
заданию подпространства
□ Теорема 1.24. Если подпространство L задано системой уравнений
L:
(31)
то
.
Доказательство.
Рассмотрим
подпространство
и покажем, что
.
Из теоремы 1.22 следует, что
(32)
Из
соотношений (31) и (32) вытекает равенство
.
Если равны два подпространства, то их
ортогональные дополнения совпадают.
Следовательно,
.
Так как
(теорема 1.23), то
.
Отсюда получаем, что
.
■
Задачи
1. Доказать, что нулевой вектор является единственным вектором из подпространства L, который ортогонален L.
2. Выяснить, ортогонален ли вектор линейной оболочке системы векторов (2,1,1,−1), (1,0,2,1), (2,1,3,−1):
а) = (1,1,1,4);
б) = (1,−3,0,1).
3. Выяснить, ортогонален ли вектор подпространству решений системы линейных уравнений
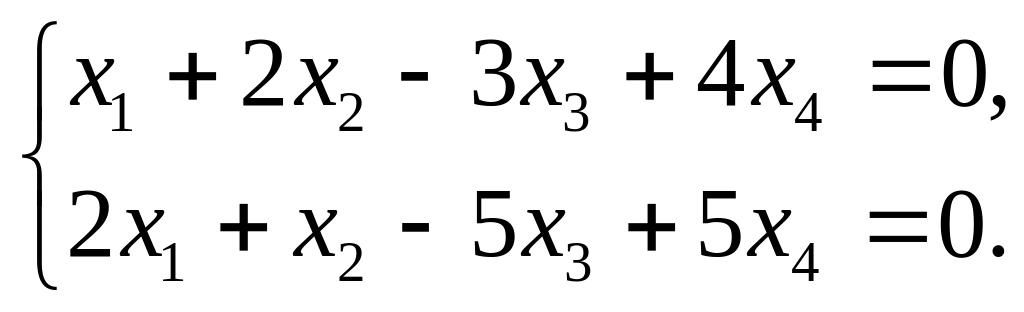
а) =(1,−4,−1,−2);
б) =(3,2,1,−1).
4. Выяснить, принадлежит ли вектор ортогональному дополнению подпространства решений системы уравнений
а) = (1,1,–1,1);
б) = (2,3,2,3).
5.
Подпространство L
задано
линейной оболочкой: L=
,
где
=(2,1,4,−2),
=(2,−1,−4,4),
=(6,−1,−4,6).
Найти базис ортогонального дополнения
6. Дано подпространство L пространства . Доказать следующие утверждения:
7. Доказать, что если подпространство L задано системой уравнений
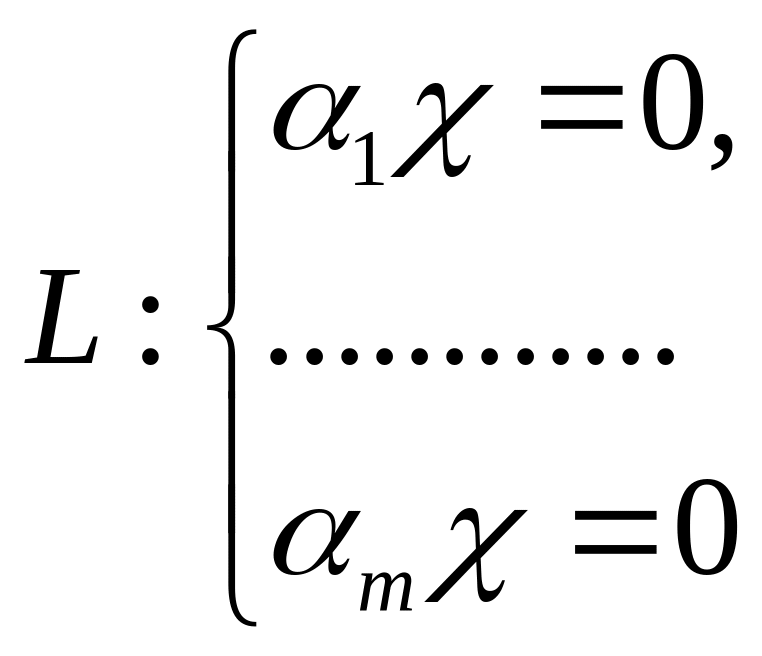
и
ее фундаментальный набор решений, то
подпространство L┴
задается следующей системой линейных
уравнений:
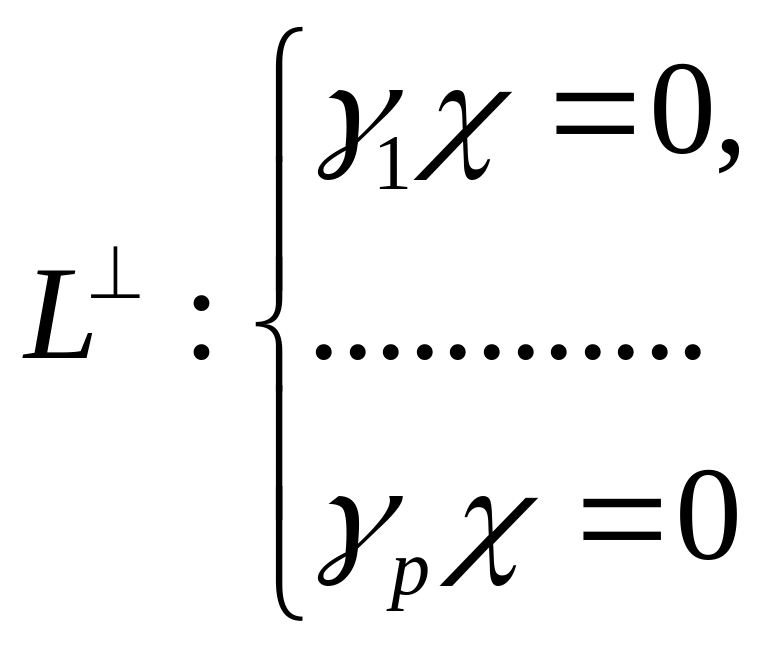
8. Дано подпространство L пространства , задано системой уравнений
и
−
фундаментальный набор решений этой
системы уравнений. Доказать, что
подпространство L
задается
системой уравнений
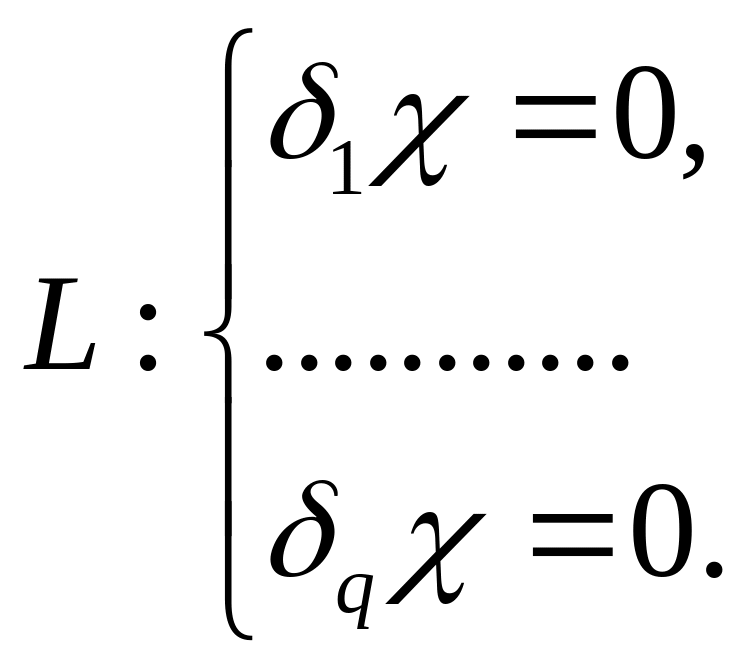
9. Подпространство L задано системой уравнений
Задать подпространство :
а) линейной оболочкой векторов;
б) системой однородных уравнений.