
- •Глава I. Векторные пространства
- •1.1. Линейная оболочка системы векторов
- •1.2. Подпространства
- •1.3. Базисы подпространств
- •Базисы пространства
- •Базисы линейной оболочки
- •Базисы подпространства решений однородной системы линейных уравнений
- •Доказать, что множество всех n-мерных векторов, у которых сумма четных координат равна сумме нечетных, образует подпространство; найти базис этого подпространства.
- •Размерность подпространства
- •1.5. Представление подпространств
- •1.6. Действия над подпространствами Пересечение подпространств
- •Сумма подпространств
- •1.7. Ортогональное дополнение
- •1.8. Ортогональные и ортонормированные базисы подпространств
Размерность подпространства
Все
базисы подпространства L
состоят
из одного и того же числа векторов.
Действительно,
пусть
![]() и
и
![]() – два базиса подпространства L.
Тогда каждая из этих систем векторов
является базисом системы векторов
– два базиса подпространства L.
Тогда каждая из этих систем векторов
является базисом системы векторов
![]() .
Теперь из теоремы 2.15 [1] следует, что
.
Теперь из теоремы 2.15 [1] следует, что
![]()
Размерностью подпространства называется число векторов в любом его базисе. Если размерность подпространства L равна k, то будем писать: dim L=k.
Примеры
1.
Из теоремы 1.5 вытекает, что
![]() .
.
2.![]() ,
так как левая и правая части равны
количеству векторов в базисе системы
(теорема 1.6).
,
так как левая и правая части равны
количеству векторов в базисе системы
(теорема 1.6).
3.
Из теоремы 1.7 следует, что размерность
подпространства решений однородной
системы уравнений
равна
![]() где n
– число неизвестных в системе уравнений,
где n
– число неизвестных в системе уравнений,
![]() –
ранг матрицы А.
–
ранг матрицы А.
□ Теорема
1.8.
Дано подпространство L,
размерность которого равна k,
и система векторов
![]() из L,
содержащая столько векторов, какова
размерность L.
Тогда следующие утверждения равносильны:
из L,
содержащая столько векторов, какова
размерность L.
Тогда следующие утверждения равносильны:
1) базис подпространства L;
2) каждый вектор подпространства L разлагается по системе векторов ;
3) система векторов линейно независимая.
Доказательство
1)![]() 2).
Вытекает из определения базиса
подпространства.
2).
Вытекает из определения базиса
подпространства.
2)
3).
Доказательство от противного.
Предположим, что система векторов
линейно зависима и
![]() − базис этой системы. Тогда
− базис этой системы. Тогда
![]() .
Из условия 2 утверждения 5 §1
[1] следует, что каждый вектор из L
разлагается по векторам
и, значит,
− базис подпространства L.
Следовательно,
.
Из условия 2 утверждения 5 §1
[1] следует, что каждый вектор из L
разлагается по векторам
и, значит,
− базис подпространства L.
Следовательно,
![]()
![]() ,
что противоречит условию теоремы.
,
что противоречит условию теоремы.
3)
1).
Доказательство от противного. Если
линейно независимая система векторов
не является базисом L,
то ее можно дополнить до базиса
подпространства L
(теорема
1.3). Следовательно,
![]() что противоречит условию теоремы. ■
что противоречит условию теоремы. ■
Пример
Выяснить,
образуют ли векторы
![]() ,
,
![]() базис подпространства
решений системы линейных уравнений
базис подпространства
решений системы линейных уравнений
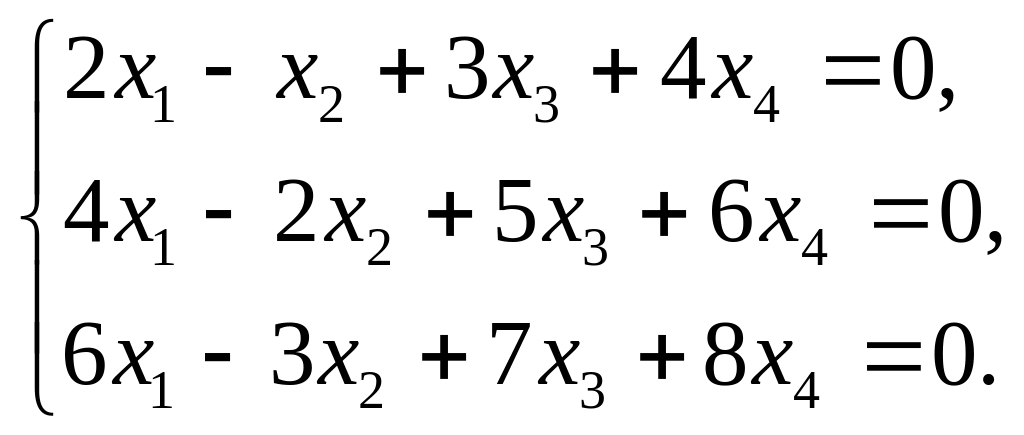
Решение.
Прежде всего
надо проверить, что векторы
и
являются решениями системы уравнений.
После подстановки координат векторов
в систему вместо неизвестных получим
верные числовые равенства. Координаты
векторов
и
не пропорциональны и, значит, они образуют
линейно независимую систему. Размерность
подпространства
равна
![]() ,
где
,
где
![]() основная
матрица системы уравнений,
основная
матрица системы уравнений,
![]() число
неизвестных в системе уравнений. Ранг
матрицы
равен двум,
число
неизвестных в системе уравнений. Ранг
матрицы
равен двум,
![]() ,
а поэтому
,
а поэтому
![]() .
Теперь из теоремы 1.8 следует, что векторы
.
Теперь из теоремы 1.8 следует, что векторы
![]() будут базисом подпространства
.
будут базисом подпространства
.
Весьма часто необходимо знать, когда два подпространства, из которых одно содержится в другом, совпадают.
□ Теорема
1.9. Пусть
![]() и
и
![]() подпространства пространства
и
подпространства пространства
и
![]() .
Тогда справедливы следующие утверждения:
.
Тогда справедливы следующие утверждения:
1.![]()
![]()
![]() .
.
2. = = .
Доказательство
1.
Пусть
![]() − базис подпространства
и, значит, линейно независимая система
векторов. Из условия
− базис подпространства
и, значит, линейно независимая система
векторов. Из условия
![]() вытекает, что векторы
принадлежат подпространству
,
а, следовательно, линейно независимую
систему векторов
можно дополнить до базиса
.
Отсюда следует, что dim
L
вытекает, что векторы
принадлежат подпространству
,
а, следовательно, линейно независимую
систему векторов
можно дополнить до базиса
.
Отсюда следует, что dim
L![]() ≤ dim
L
≤ dim
L![]() .
.
2.
Необходимость.
Пусть dim
L
=
dim
L
=
k
и
![]() − базис подпространства
.
Из условия
следует, что линейно независимые векторы
− базис подпространства
.
Из условия
следует, что линейно независимые векторы
![]() принадлежат
,
и система
содержит столько векторов, какова
размерность подпространства
.
Из теоремы 1.8 вытекает, что система
векторов
− базис
.
Итак,
и
обладают общим базисом и, значит,
принадлежат
,
и система
содержит столько векторов, какова
размерность подпространства
.
Из теоремы 1.8 вытекает, что система
векторов
− базис
.
Итак,
и
обладают общим базисом и, значит,
![]() (следствие из теоремы 1.2).
(следствие из теоремы 1.2).
Достаточность.
Если
,
то они имеют общий базис и dim
L
![]() dim
L
.
■
dim
L
.
■
Следствие. Если − подпространство пространства , то справедливы следующие утверждения:
1.
![]() ;
;
2.
![]() .
.
Доказательство
Заметим,
что
![]() и n
dim
.
Теперь следствие есть частный случай
теоремы, когда
и n
dim
.
Теперь следствие есть частный случай
теоремы, когда
![]() и
и
![]() .
.
Задачи
1.
Подпространство
имеет размерность
![]() .
Доказать, что ранг системы векторов
,
принадлежащих подпространству
,
не больше
.
.
Доказать, что ранг системы векторов
,
принадлежащих подпространству
,
не больше
.
2. Доказать, что подпространство является линейной оболочкой системы векторов из подпространства тогда и только тогда, когда размерность равна рангу системы векторов .
3. Подпространство имеет размерность и является линейной оболочкой системы векторов . Доказать, что − базис подпространства .
4.
Подпространство
содержится в подпространстве
![]() и
линейно независимые векторы из
подпространства
.
Доказать, что
,
если размерность
равна
.
и
линейно независимые векторы из
подпространства
.
Доказать, что
,
если размерность
равна
.
5. Сформулировать алгоритм, позволяющий установить совпадение двух подпространств и в следующих случаях:
а) и − линейные оболочки системы векторов;
б) и − подпространства решений однородной системы линейных уравнений;
в)
![]() ;
;
![]() .
.
6.
Выяснить, совпадет ли пространство
![]() с линейной оболочкой
с линейной оболочкой
![]() :
:
а)
![]() ;
;
б)
![]() .
.
7.
Выяснить, совпадают ли подпространства
и
пространства
![]() ,
где
задано системой уравнений
,
где
задано системой уравнений
![]()
а
− линейная оболочка системы векторов
![]() .
.
8.
Система векторов
эквивалентна базису
подпространства
.
Доказать, что
![]() базис
подпространства
.
базис
подпространства
.
