
- •Глава I. Векторные пространства
- •1.1. Линейная оболочка системы векторов
- •1.2. Подпространства
- •1.3. Базисы подпространств
- •Базисы пространства
- •Базисы линейной оболочки
- •Базисы подпространства решений однородной системы линейных уравнений
- •Доказать, что множество всех n-мерных векторов, у которых сумма четных координат равна сумме нечетных, образует подпространство; найти базис этого подпространства.
- •Размерность подпространства
- •1.5. Представление подпространств
- •1.6. Действия над подпространствами Пересечение подпространств
- •Сумма подпространств
- •1.7. Ортогональное дополнение
- •1.8. Ортогональные и ортонормированные базисы подпространств
1.6. Действия над подпространствами Пересечение подпространств
Пусть даны подпространства и векторного пространства . Совокупность всех векторов пространства , которые принадлежат и , и , называется пересечением подпространств и , т. е.
![]() .
.
□ Теорема 1.13. Пересечение подпространств и пространства является подпространством.
Доказательство.
Пусть
и
– произвольные векторы из множества
![]() .
Из определения пересечения подпространств
вытекает, что
.
Из определения пересечения подпространств
вытекает, что
![]() и
и
![]() .
Отсюда и из определения подпространства
вытекает
.
Отсюда и из определения подпространства
вытекает
![]() ,
,![]() ,
(5)
,
(5)
![]() ,
,
![]() .
(6)
.
(6)
Теперь
из равенств (5)–(6) получаем, что
![]() ,
,
![]() ,
т. е.
–
подпространство пространства
.
■
,
т. е.
–
подпространство пространства
.
■
Чтобы найти пересечение подпространств и достаточно задать подпространство в виде линейной оболочки системы векторов или в виде множества решений однородной системы уравнений.
□ Теорема 1.14. Если подпространства и заданы в виде множества решений системы линейных уравнений
![]() ,
,
![]() ,
,
то
подпространство
совпадает
множеством решений системы уравнений
![]()
Доказательство. Действительно,
![]()
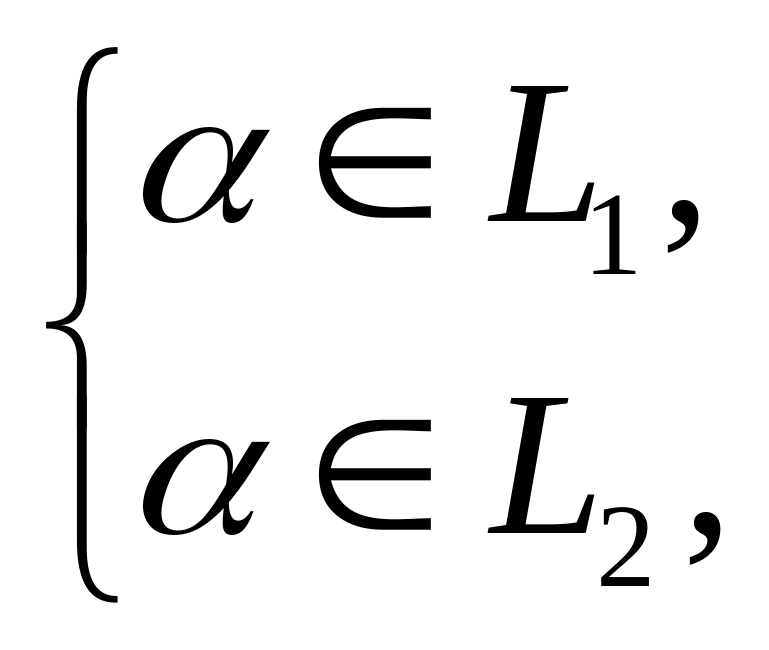 Û
Û
![]() Û
Û
![]() − решение
системы уравнений
■
− решение
системы уравнений
■
Пример
Даны
линейная оболочка
![]() и подпространство
решений системы линейных уравнений
и подпространство
решений системы линейных уравнений
![]() .
Доказать, что пересечение
.
Доказать, что пересечение
![]() ,
,
где
матрица,
столбцами которой являются координаты
векторов системы
,
система векторов
![]() фундаментальный набор решений системы
уравнений
фундаментальный набор решений системы
уравнений
![]()
Решение вытекает из следующей цепочки равносильных утверждений:
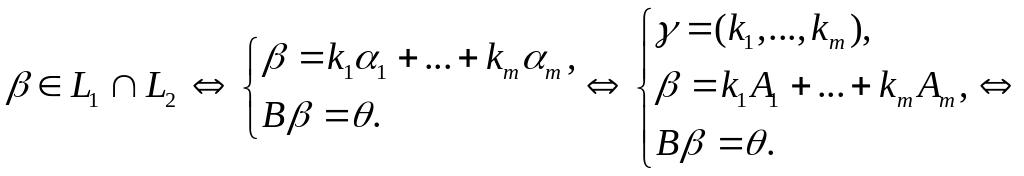
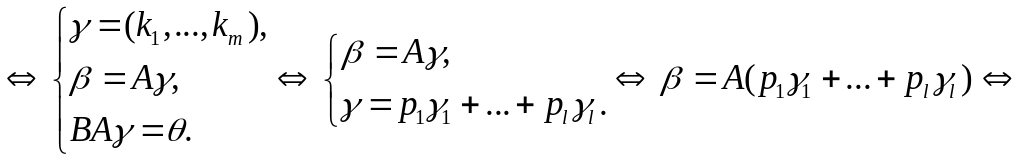
![]()
В дальнейшем изучении курса полезно будет знать, когда пересечение подпространств совпадает с нулевым подпространством.
□ Теорема
1.15. Даны
подпространства
и
![]() – базис
,
– базис
.
Пересечение подпространств
и
совпадает с нулевым подпространством
тогда и только тогда, когда объединение
базисов
,
подпространств
и
является линейно независимой системой
векторов.
– базис
,
– базис
.
Пересечение подпространств
и
совпадает с нулевым подпространством
тогда и только тогда, когда объединение
базисов
,
подпространств
и
является линейно независимой системой
векторов.
Необходимость.
Дано, что
![]() .
Докажем линейную независимость системы
векторов
,
.
Пусть
.
Докажем линейную независимость системы
векторов
,
.
Пусть
![]() (7)
(7)
произвольное разложение вектора по системе векторов , . Рассмотрим вектор
![]() (8)
(8)
Вектор
разлагается по базису подпространства
и, значит,
![]() .
С другой стороны, из равенств (7) и
(8) следует, что
.
С другой стороны, из равенств (7) и
(8) следует, что
![]() .
(9)
.
(9)
Из
равенства (9) вытекает, что вектор
разлагается по базису
подпространства
,
а поэтому вектор
![]() .
Итак, вектор
.
Итак, вектор
![]() и, значит,
и, значит,
![]() .
Отсюда и из равенств (8) и (9) получаем
.
Отсюда и из равенств (8) и (9) получаем
![]() (10)
(10)
![]() (11)
(11)
Теперь
из линейной независимости систем
векторов
и
,
равенств (10) и (11) вытекает
![]() .
.
Этим
доказана линейная независимость системы
векторов
![]() .
.
Достаточность.
Дано
– линейно независимая система векторов.
Покажем, что
![]() .
Пусть
.
Пусть
![]() −
произвольный вектор из подпространства
−
произвольный вектор из подпространства
![]() .
Тогда вектор
.
Тогда вектор
![]() ,
,
а поэтому вектор
разлагается
как по базису подпространства
,
так и по базису подпространства
,
т. е.
,
,
а поэтому вектор
разлагается
как по базису подпространства
,
так и по базису подпространства
,
т. е.
![]() (12)
(12)
![]() (13)
(13)
Из
равенств (12) и (13) вытекает, что
![]() (14)
(14)
Теперь
из линейной независимости системы
векторов
и равенства (14) получаем
![]() .
Отсюда из равенства (12) следует, что
.
Отсюда из равенства (12) следует, что
![]() .
Этим установлено, что
.
■
.
Этим установлено, что
.
■
Следствие.
Даны
линейно независимые системы векторов
![]() и
и
![]() .
Пересечение линейных оболочек
.
Пересечение линейных оболочек
![]() и
и
![]() равно нулевому подпространству тогда
и только тогда, когда
,
– линейно независимая система векторов.
равно нулевому подпространству тогда
и только тогда, когда
,
– линейно независимая система векторов.
Доказательство.
Утверждение
следствия вытекает из теоремы 1.15, так
как
и
–
базисы соответственно подпространств
и
![]()
